 |
Расчеты на прочность при изгибе
|
|
|
|
При прямом поперечном изгибе балки в ее поперечных сечениях возникают нормальные σ и касательные напряжения τ.
Нормальные напряжения в любом слое произвольного поперечного сечения можно определить по формуле Навье:
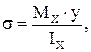(3.1)
где МХ - изгибающий момент в рассматриваемом сечении;
у – текущая ордината до рассматриваемого слоя поперечного сечения, отсчитываемая от нейтральной оси сечения;
IX – осевой момент инерции поперечного сечения.
Из анализа формулы (4.1) следует:
− нормальные напряжения по высоте сечения изменяются по линейному закону, то есть эпюра нормальных напряжений очерчивается наклонной прямой, проходящей через центр тяжести сечения.
− наибольшие нормальные напряжения возникают в волокнах балки, наиболее удаленных от нейтральной оси.
Знак нормальных напряжений определяется знаком изгибающего момента в рассматриваемом сечении. Если сжаты верхние волокна балки (положительное значение изгибающего момента), то в них соответственно будут возникать сжимающие нормальные напряжения со знаком «минус». Нижние волокна балки будут растянуты, а действующие в них нормальные напряжения будут положительными.
Оценка прочности по нормальным напряжениям для балки постоянной жесткости производится по формуле
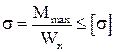, (3.2)
где Mmах − наибольший (по абсолютной величине) изгибающий момент;
Wx – осевой момент сопротивления поперечного сечения балки;
[σ] – допускаемое напряжение для заданного материала.
Для определения касательных напряжений в любом слое произвольного поперечного сечения при изгибе используется формула Журавского:
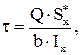(3.7)
где Q − поперечная сила в рассматриваемом сечении;
|
|
|
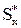− статический момент части сечения, находящейся над исследуемым слоем;
b− ширина исследуемого слоя;
Ix – осевой момент инерции поперечного сечения.
Касательные напряжения по высоте сечения изменяются по параболическому закону, причем своего максимального значения они достигают в нейтральном слое. Знак касательного напряжения зависит от знака действующей в рассматриваемом сечении поперечной силы.
Оценка прочности балки по касательным напряжениям для балки постоянной жесткости производится по условию прочности:
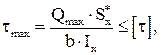(3.8)
где Qmax – наибольшая (по абсолютной величине) поперечная сила.
При прямом поперечном изгибе материал балки в общем случае испытывает плоское напряженное состояние. Оценка прочности материала балки в опасной точке опасного сечения выполняется с применением III и IV теорий прочности:
(3.9)
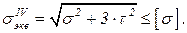(3.10)
При этом следует учитывать, что для проверки прочности по эквивалентным напряжениям опасным сечением является такое сечение, в котором одновременно действуют максимальный изгибающий момент и поперечная сила. Причем следует учитывать, что изгибающий момент вызывает более значительные напряжения. Если такое сечение отсутствует, то необходимо проводить проверку по нескольким сечениям.
Главные напряжения вычисляются по формуле
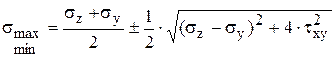, (3.11)
где σz,σy,τxy – действующие в опасном сечении нормальные и касательное напряжения.
Главные напряжения обозначаются σ1, σ2, σ3, соотношение между которыми следующее:
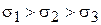. (3.12)
При плоском напряженном состоянии одно из главных напряжений равно нулю. Главные напряжения действуют на главных площадках, положение которых определяется углом поворота α:
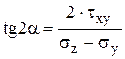. (3.13)
Положительный угол α обеспечивается поворотом исходных площадок против хода часовой стрелки. Максимальное главное напряжение действует по той грани, по которой в исходном состоянии действовало максимальное исходное напряжение и которую повернули на угол α и направлено оно будет в ту сторону, где как бы сходятся касательные напряжения.
|
|
|
|
|
|
