 |
Таблица 4.1
|
|
|
|
Рис. 4. 1
Во время работы активный шаг помечается маркером (выделяется).
Начальная ситуация программы SFC описывается начальными шагами. Начальный шаг обозначается графическим символом с двойной рамкой. После запуска программы маркер автоматически устанавливается на каждый начальный шаг (рис. 4. 2).
Рис. 4. 2
У каждого шага есть атрибуты. Они могут быть использованы в любом другом языке в любом месте программы:
GSnnn. x. ........... активность шага (логическая переменная);
GSnnn. t. ........... продолжительность активного состояния шага (таймер),
где nnn – номер шага.
Переходы представлены горизонтальными полосками (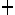 
), которые пересекают линии связи. Каждому переходу присвоен номер, следующий за символом перехода. Описание перехода (комментарий) располагается справа от символа перехода. Вышеприведенная информация называется Уровнем 1 перехода (рис. 4. 3).
Рис. 4. 3
Для связи шагов и переходов используются одиночные линии. Это ориентированные связи. Когда ориентация не задана явно, связь ориентирована сверху вниз (рис. 4. 4).
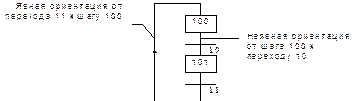
Рис. 4. 4
Символ прыжка 
может быть использован, чтобы определить линию
связи от перехода к шагу, не рисуя линию. Символ прыжка должен иметь номер шага назначения (рис. 4. 5).
Рис. 4. 5
Связь от шага к переходу нельзя представить с помощью символа прыжка.
Расхождения – это множественные связи от одного символа SFC (шага или перехода) ко многим. Схождение – это множественные связи от более чем одного символа SFC к одному другому символу. Схождения и расхождения могут быть одиночными или двойными.
Одиночное расхождение – это множественная связь от одного шага к нескольким переходам. Оно позволяет маркеру активности пройти по одной из множества ветвей. Одиночное схождение - это множественная связь от нескольких переходов к одному и тому же шагу. Одиночное схождение, обычно используется для того, чтобы объединить несколько ветвей SFC, начавшихся из одиночного расхождения. Одиночные расхождения и схождения обозначаются одиночными горизонтальными линиями (рис. 4. 6).
|
|
|
Рис. 4. 6
Следует обратить внимание, что условия, присоединённые к переходам, не являются взаимоисключающими. Для того чтобы программа пошла по одной ветке, надо явно определить исключительность условий перехода.
Двойное расхождение – это множественная связь от одного перехода к нескольким шагам. Она соответствует параллельной работе процесса. Двойное схождение – это множественная связь от нескольких шагов к одному и тому же переходу. Двойное схождение, обычно, используется для того, чтобы объединить несколько ветвей SFC, начавшихся из двойного
расхождения. Двойные расхождения и схождения обозначаются двойными горизонтальными линиями (рис. 4. 7).
Рис. 4. 7
Уровень 2 шага SFC представляет собой детальное описание действий в период активности шага. Это описание может использовать текстовые дополнения языка SFC или язык ST. Основные типы действий: булевские действия; импульсные действия, описанные на ST (действия типа " Р" ); не сохраняемые действия, описанные на ST (действия типа " N" ); SFC действия.
Булевские действия присваивают значение логической переменной при активизации шага. Логические переменные могут быть выходными или внутренними. Им присваивается значение каждый раз, когда шаг становится активным или перестаёт быть активным. Синтаксис основных логических действий показан в табл. 4. 1.
Таблица 4. 1
| Логическое действие | Описание |
| . < boolean_variable> (N); < boolean_variable> ; | Присвоить переменной сигнал активности шага |
| / < boolean_variable> ; | Присвоить переменной отрицание сигнала активности шага |
| < boolean_variable> (S); | Присваивает переменной значение TRUE, когда шаг становится активным |
| < boolean_variable> (R); | Присваивает переменной значение FALSE, когда шаг становится активным |
|
|
|
Импульсное действие – это список инструкций ST или IL, которые выполняются только однажды при активизации шага. Инструкции пишутся в соответствии со следующим синтаксисом:
|
|
|
