 |
Уравнение Шредингера. Волновая функция
|
|
|
|
– стационарное уравнение Шредингера;
– вероятность обнаружить частицу в объеме dV;
– условие нормировки волновой функции;
– решение уравнения Шредингера для частицы в одномерном потенциальном ящике с бесконечно высокими стенками, где:
; 
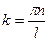– модуль волнового вектора;
– амплитуда волновой функции;
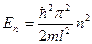– энергия частицы в одномерном потенциальном ящике с бесконечно высокими стенками, где n – квантовое число, принимающее значения: n =1, 2, 3, …∞.
– полная энергия электрона в атоме водорода, где n – главное квантовое число, принимающее значения n =1, 2, … ∞;
– спиновый (собственный) момент импульса (механический момент) электрона в атоме водорода, где s – спиновое квантовое число, s =1/2;
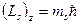– проекция механического спинового момента электрона в атоме водорода на выделенное направление, где ms – магнитное квантовое число, принимающее значения: ms =±1/2;
– орбитальный момент импульса (механический момент) электрона в атоме водорода, где l – орбитальное квантовое число, принимающее значения: l =0 (s-орбиталь); l =1 (p-орбиталь); l =2 (d-орбиталь); … l = n –1;
– проекция механического орбитального момента электрона в атоме водорода на выделенное направление, где ml – магнитное квантовое число, принимающее значения: ml =0, ±1, ±2, … ± l;
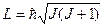– полный момент импульса (механический момент) электрона в атоме, где J – квантовое число полного момента, J =| l – s |, | l – s |+1, … l+s.
376. # Поток электронов падает на экран с двумя щелями. В точке Р за экраном находится входное отверстие счетчика. Пусть А 1 – амплитуда волны, прошедшей через первую щель и достигшей точки Р, а А 2 – то же, но в случае открытой щели 2.Отношение амплитуд А 2/ А 1=3. Если открыта только щель 1, то счетчик регистрирует 100 электронов в секунду. Сколько электронов ежесекундно будет регистрировать счетчик, если а) открыта только щель 2; б) открыты обе щели и в точке Р наблюдается интерференционный максимум; в) открыты обе щели и в точке Р наблюдается интерференционный минимум?
|
|
|
377. # Частица находится в прямоугольном одномерном потенциальном ящике шириной l с бесконечно высокими стенками. Найти нормированные волновые функции стационарных состояний частицы.
378. Электрон находится в прямоугольном одномерном потенциальном ящике с бесконечно высокими стенками. Ширина ящика 0.2 нм, энергия электрона 37.8 эВ. Определить номер n энергетического уровня и модуль волнового вектора k.
379. Частица находится в прямоугольном одномерном потенциальном ящике с бесконечно высокими стенками в основном состоянии. Какова вероятность обнаружения частицы: а) в средней трети ящика; б) в крайней трети ящика?
380. # Частица находится в прямоугольном одномерном потенциальном ящике с бесконечно высокими стенками. Найти отношение разности ΔEn,n+1 соседних энергетических уровней к энергии En частицы в трех случаях: а) n= 2; б) n= 5; в) n→∞.
381. Электрон находится в бесконечно глубоком прямоугольном одномерном потенциальном ящике шириной 0.1 нм. Определить наименьшую разность энергетических уровней электрона. Выразить в эВ.
382. # Частица в бесконечно глубоком прямоугольном одномерном потенциальном ящике шириной l находится в возбужденном состоянии с квантовым числом 3. Определить, в каких точках интервала 0< x < l плотность вероятности нахождения частицы имеет максимальное и минимальное значения.
383. # Волновая функция, описывающая движение электрона в основном состоянии атома водорода, имеет вид ψ (r)= Aexp (– r / а 0), где А – некоторая постоянная, а 0=53 пм – первый Боровский радиус. Найти для основного состояния атома водорода наиболее вероятное расстояние электрона от ядра.
|
|
|
384. Электрон находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Найти ширину ямы, если разность энергии между уровнями с квантовыми числами 2 и 3 составляет 0.3 эВ.
385. # Волновая функция частицы массой m для основного состояния в одномерном потенциальном поле U (x)= kx2 /2 имеет вид ψ (x)= Aexp (– αx 2), где A и α – некоторые постоянные. Найти с помощью уравнения Шредингера постоянную α и энергию частицы в этом состоянии.
386. # Найдите энергию и орбитальный момент импульса электрона в атоме водорода, соответствующие состояниям: а) 1 s; б) 2 s; в) 2 p.
387. # Найдите проекции орбитального момента импульса электрона на направление индукции магнитного поля, соответствующие l =2.
388. # Найдите проекции спинового момента импульса электрона на направление индукции магнитного поля.
389. * Чему равен максимальный возможный полный механический момент атома лития, валентный электрон которого находится в состоянии с n =3?
390. * Чему равен максимальный возможный полный механический момент атома натрия, валентный электрон которого находится в состоянии с n =4?
10. Ядро и элементарные частицы
– дефект массы;
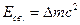– энергия связи ядра;
– удельная энергия связи;
– закон радиоактивного распада;
– период полураспада;
– среднее время жизни радиоактивного ядра;
– активность изотопа.
391. Какую энергию нужно затратить для отрыва нейтрона от ядра 11Na24?
392. Найти энергию связи, удельную энергию связи и дефект массы ядра изотопа углерода 6С12.
393. Найти постоянную распада радия, если период полураспада 1550 лет.
394. Период полураспада фосфора Р32 – 15 дней. Найти активность препарата через 10, 20 и 90 дней после его изготовления, если начальная активность равна 100 мКи.
395. Активность некоторого препарата уменьшается в 2.5 раза за 7 суток. Найти его период полураспада.
396. # Вычислить число атомов радона Rn222, распавшихся в течение первых суток, если первоначальная масса радона равна 1 г. Период полураспада равен 3.82 суток. Найти постоянную распада радона.
397. Первоначальная масса урана 92U238 равна 1 г. Найти начальную активность и активность через 1 миллион лет. Период полураспада 4.5.109 лет.
398. Радиоактивный натрий 11Na27 распадается, выбрасывая электроны. Период полураспада натрия 14.8 часа. Вычислить количество атомов, распавшихся в 1 мг данного радиоактивного препарата за 10 часов.
|
|
|
399. Определить период полураспада радона, если за сутки из 1 миллиона атомов распадается 175 тысяч атомов.
400. Сколько процентов от начального количества радиоактивного химического элемента распадается за время, равное средней продолжительности жизни ядер этого элемента?
401. Активность изотопа углерода 6С14 в древних деревянных предметах составляет 80% активности этого изотопа в свежесрубленных деревьях. Период полураспада равен 5570 годам. Определить возраст древних предметов.
402. # В результате захвата α–частицы ядром изотопа азота 7N14 образуются неизвестный элемент и протон. Написать реакцию, определить неизвестный элемент и найти энергетический эффект реакции.
403. В результате захвата нейтрона ядром изотопа азота 7N14 образуются неизвестный элемент и α–частица. Написать реакцию и определить неизвестный элемент.
404. При бомбардировке изотопа азота 7N14 нейтронами получается изотоп углерода 6С14, который оказывается β–радиоактивным. Написать уравнения обеих реакций.
405. Изотоп радия с массовым числом 226 превратился в изотоп свинца с массовым числом 206. Сколько α– и β–распадов произошло при этом?
406. # Точечный источник γ–излучения Co60 (период полураспада 5.3 года) находится в центре сферического свинцового контейнера с толщиной стенок 1 см и наружным радиусом 20 см. Определить интенсивность потока на выходе контейнера, если активность препарата 100 мкКи, при каждом распаде выделяется два γ–кванта, а линейный коэффициент поглощения равен 0.64 см-1.
407. Сколько энергии выделится при образовании одного грамма гелия из протонов и нейтронов?
408. # Определить энергию реакции B10(n, α)3Li7, протекающей в результате взаимодействия весьма медленных нейтронов с покоящимися ядрами бора. Найти кинетические энергии продуктов реакции.
409. Найти энергию реакции 4Be9+1H1 → 2He4+3Li6, если кинетическая энергия протона равна 5.45 МэВ, ядра гелия – 4 МэВ. Ядро гелия вылетело под углом 900 к направлению движения протона, ядро-мишень неподвижно.
|
|
|
410. Какая энергия выделится, если при реакции 4Be9+1H2 → 5В10+0n1 подвергнуть превращению все ядра, находящиеся в одном грамме бериллия?
411. Какое количество энергии можно получить от деления 1 г урана 92U238, если при каждом делении выделяется энергия, приблизительно равная 200 МэВ?
412. Определить энергетический эффект реакции 7N14+2He4→ 8О17+1H1. Выделяется или поглощается энергия?
413. # Атомный ледокол имеет мощность 32 МВт и потребляет в сутки 200 г урана 92U235. Определить коэффициент полезного действия реактора ледокола.
414. Какое количество энергии выделяется в результате термоядерной реакции синтеза 1 г гелия из дейтерия и трития?
415. Вычислить энергию, необходимую для разделения ядра Ne20 на две α–частицы и ядро С12, если удельная энергия связи в ядрах неона, гелия и углерода равна 8.03, 7.07 и 7.68 МэВ соответственно.
416. Определить энергию реакции 3Li7+p→22He4, если удельная энергия связи в ядрах лития и гелия равны 5.6 и 7.06 МэВ соответственно.
417. При бомбардировке изотопа алюминия 13Al27 α–частицами получается радиоактивный изотоп фосфора 15Р30, который затем распадается с испусканием позитронов. Написать уравнения обеих реакций.
418. При образовании электрона и позитрона из фотона энергия фотона была равна 2.62 МэВ. Чему была равна в момент возникновения полная кинетическая энергия позитрона и электрона?
419. # Электрон и позитрон, образованные квантом с энергией 5.7 МэВ, дают в камере Вильсона, помещенной в магнитное поле, траектории с радиусом кривизны 3 см. Найти индукцию магнитного поля.
420. Определить пороговую энергию γ–кванта для образования электронно-позитронной пары в кулоновском поле ядра.
Таблица. Массы легких атомов.
| Z | Атом | Избыток массы атома М-А, а.е.м. | Z | Атом | Избыток массы атома М-А, а.е.м. |
| n 1H 2H 3H 3He 4He 6Li 7Li 7Be 8Be 9Be 10Be 10B 11B | 0.00867 0.00783 0.01410 0.01605 0.01603 0.00260 0.01513 0.01601 0.01693 0.00531 0.01219 0.01354 0.01294 0.00930 | 11C 12C 13C 13N 14N 15N 15O 16O 17O 19F 20Ne 23Na 24Na 24Mg | 0.01143 0.00335 0.00574 0.00307 0.00011 0.00307 -0.00509 -0.00087 -0.00160 -0.00756 -0.01023 -0.00903 -0.01496 | ||
| Здесь М – масса атома в а.е.м., А – массовое число. |
Библиографический список
1. Волькенштейн, В.С. Сборник задач по общему курсу физики / В.С.Волькенштейн. – СПб.: Лань, 1999. – 328 с.
2. Иродов, И.Е. Задачи по общей физике: учебное пособие / И.Е.Иродов. – СПб.: Лань, 2001. – 416 с.
3. Савельев, И.В. Сборник вопросов и задач по общей физике: учеб. пособие для студентов высш. техн. учеб. заведений / И.В.Савельев. – М.: АСТ, 2001. – 318 с.
|
|
|
4. Сахаров, Д.И. Сборник задач по физике для вузов / Д.И.Сахаров. – М.: Мир и Образование, 2003. – 400 с.
5. Чертов, А.Г. Задачник по физике: учеб. пособие / А.Г.Чертов, А.А. Воробьев. – 4-е изд., перераб. и доп. – М.: Высш. школа, 1981. – 496 с.
6. Калашников, Н.П. Основы физики. Упражнения и задачи: учеб. пособие для вузов / Н.П.Калашников, М.А. Смондырев. – М.: Дрофа, 2004. – 464 с.
7. Калашников, Н.П. Основы физики: учеб. для вузов: в 2 т. / Н.П.Калашников, М.А.Смондырев. - 2-е изд., перераб. – М.: Дрофа, 2003.
8. Детлаф, А.А. Курс физики: учеб. пособие для вузов / А.А. Детлаф, В.М. Яворский. - М.: Высш.шк., 1989.- 608 с.
9. Савельев, И.В. Курс общей физики: в 3 т. Т. 1: Механика. Молекулярная физика / И. В. Савельев. - М.: Наука, 1977. - 416 с.
10. Курс физики: учеб. для вузов: в 2 т. Т. 1 / под ред. В.Н.Лозовского. – СПб.: Лань, 2000. – 576 с.
11. Трофимова, Т.И. Курс физики / Т.И. Трофимова.-М.: Высш. шк., 1999.-542 с.
СОДЕРЖАНИЕ
Требования к оформлению и общие методические указания по выполнению индивидуальных домашних заданий…………………………..………….….…..3
1. Геометрическая оптика и фотометрия………………………………………4
2. Интерференция………………………..……………………………………..10
3. Дифракция………………………………………………………………....…17
4. Поляризация, поглощение…………………………………………………..23
5. Тепловое излучение…………………………………………………………28
6. Квантовые свойства света…………………………………………………. 32
7. Строение атома…………………………………………………………..….36
8. Волновые свойства частиц…………………………………………….…...40
9. Уравнение Шрёдингера. Волновая функция…………………………….. 43
10. Ядро и элементарные частицы………………………………………….…..45
Библиографический список………………….…………………………….……..48
|
|
|
