Главная | Обратная связь | Поможем написать вашу работу!
 МегаЛекции

Основные требования к оформлению контрольной работы.

1. Работа должна быть выполнена в ученической тетради, аккуратно и разборчиво.

2. Решение заданий желательно располагать в порядке номеров, указанных в задании; номера следует указывать перед условием.

3. Условия заданий обязательно переписываются полностью.

4. При оформлении записей необходимо выполнять общие требования к культуре их ведения.

5. Решения заданий должны сопровождаться краткими, но достаточно обоснованными пояснениями; используемые формулы нужно выписывать.

6. После выполнения каждого задания необходимо оставлять свободное место для замечаний преподавателя.

7. Если в работе допущены недочеты и ошибки, контрольная работа возвращается студенту на доработку.

8. Контрольные работы должны быть выполнены в срок.

9. При возникновении затруднений при выполнении контрольной работы обучающиеся могут получить индивидуальную консультацию в течение семестра по графику работы преподавателя.

10. Незачтенная работа должна быть исправлена и снова сдана на проверку вместе с незачтенной работой.

11. Контрольные работы, выполненные не по своему варианту, возвращаются без проверки.

К О Н Т Р О Л Ь Н Ы Е З А Д А Н И Я

ВАРИАНТ № 1

 

  1. ВЫЧИСЛИТЬ ПРЕДЕЛЫ, НЕ ПОЛЬЗУЯСЬ ПРАВИЛОМ ЛОПИТАЛЯ:

а) б)

 

  1. ЗАДАНА ФУНКЦИЯ РАЗЛИЧНЫМИ АНАЛИТИЧЕСКИМИ ВЫРАЖЕНИЯМИ ДЛЯ РАЗЛИЧНЫХ ОБЛАСТЕЙ ИЗМЕНЕНИЯ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ. НАЙТИ ТОЧКИ РАЗРЫВА ФУНКЦИИ, ЕСЛИ ОНИ СУЩЕСТВУЮТ. СДЕЛАТЬ ЧЕРТЕЖ.
  х - 3 ,   если           х   ≤ 1,    
у = х2 + 1, если   < х ≤ 3,    
  10, если     х > 3.    

 

  1. НАЙТИ ПРОИЗВОДНУЮ ФУНКЦИИ В ТОЧКЕ х = 3, =

 

  1. НАЙТИ ЧАСТНЫЕ ПРОИЗВОДНЫЕ 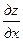; 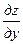ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ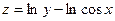

 
  1. НАЙТИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ:
  1. НАЙТИ ПУТЬ, ПРОЙДЕННЫЙ ТЕЛОМ ЗА ПЕРВЫЕ 5 С ОТ НАЧАЛА ДВИЖЕНИЯ, ЕСЛИ СКОРОСТЬ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ ЗАДАНА УРАВНЕНИЕМ 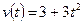(м/с) м/с..

 

 

  1. НАЙТИ ОБЩЕЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПЕРВОГО

ПОРЯДКА:

 

  1. ВЫЧИСЛИТЬ ВЫБОРОЧНЫЕ СРЕДНЕЕ, ДИСПЕРСИЮ И СРЕДНЕКВАДРАТИЧНОЕ ОТКЛОНЕНИЕ ДЛЯ СЛЕДУЮЩЕЙ ВЫБОРКИ:

хί: 6,26; 3,82; 5,47; 4,46; 4,76; 4,78; 4,12; 6,04; 5,12; 5,23; 5,21; 5,85.

 

 

ВАРИАНТ № 2

 

  1. ВЫЧИСЛИТЬ ПРЕДЕЛЫ, НЕ ПОЛЬЗУЯСЬ ПРАВИЛОМ ЛОПИТАЛЯ:

а) б)

 

 

  1. ЗАДАНА ФУНКЦИЯ РАЗЛИЧНЫМИ АНАЛИТИЧЕСКИМИ ВЫРАЖЕНИЯМИ ДЛЯ РАЗЛИЧНЫХ ОБЛАСТЕЙ ИЗМЕНЕНИЯ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ. НАЙТИ ТОЧКИ РАЗРЫВА ФУНКЦИИ, ЕСЛИ ОНИ СУЩЕСТВУЮТ. СДЕЛАТЬ ЧЕРТЕЖ.
  -х- 0,5,   если           х   ≤ -1,    
у = 2х, если -1 < х ≤ 3,    
  - 2х + 3, если     х > 3.    

 

  1. НАЙТИ ЗНАЧЕНИЕ ПРОИЗВОДНОЙ ФУНКЦИИ , ПРИ х = −1

=

 

  1. НАЙТИ ЧАСТНЫЕ ПРОИЗВОДНЫЕ 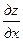; 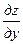ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

z =

 

 

  1. НАЙТИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ:

 

  1. ТЕЛО ДВИЖЕТСЯ ПО ПРЯМОЙ СО СКОРОСТЬЮ (м/с), ВЫЧИСЛИТЕ ПУТЬ, ПРОЙДЕННЫЙ ТЕЛОМ ЗА 4-УЮ СЕКУНДУ ОТ НАЧАЛА ДВИЖЕНИЯ.

 

 

  1. НАЙТИ ОБЩЕЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПЕРВОГО

ПОРЯДКА:

 

 

  1. ВЫЧИСЛИТЬ ВЫБОРОЧНЫЕ СРЕДНЕЕ, ДИСПЕРСИЮ И СРЕДНЕКВАДРАТИЧНОЕ ОТКЛОНЕНИЕ ДЛЯ СЛЕДУЮЩЕЙ ВЫБОРКИ:

 

хί: 1,13; 1,14; 1,22; 1,05; 0,88; 0,76;1,14; 1,05; 1,23; 0,91; 1,44; 0,96.

ВАРИАНТ № 3

 

  1. ВЫЧИСЛИТЬ ПРЕДЕЛЫ, НЕ ПОЛЬЗУЯСЬ ПРАВИЛОМ ЛОПИТАЛЯ:

а) 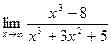б)

 

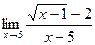
  1. ЗАДАНА ФУНКЦИЯ РАЗЛИЧНЫМИ АНАЛИТИЧЕСКИМИ ВЫРАЖЕНИЯМИ ДЛЯ РАЗЛИЧНЫХ ОБЛАСТЕЙ ИЗМЕНЕНИЯ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ. НАЙТИ ТОЧКИ РАЗРЫВА ФУНКЦИИ, ЕСЛИ ОНИ СУЩЕСТВУЮТ. СДЕЛАТЬ ЧЕРТЕЖ.
  х3 - 1,   если           х   < 0,    
у = - х + 3, если   ≤ х ≤ 4,    
  -1, если     х > 4.    

 

3. НАЙТИ ЗНАЧЕНИЕ ПРОИЗВОДНОЙ ФУНКЦИИ , ПРИ х = −3 =

  1. НАЙТИ ЧАСТНЫЕ ПРОИЗВОДНЫЕ 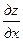; 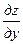ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

.

 

 

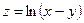  1. НАЙТИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ:

 

  1. ВЫЧИСЛИТЬ ПЛОЩАДЬ ФИГУРЫ, ОГРАНИЧЕННОЙ ЛИНИЯМИ:

у2 = 9х, х = 16, х = 25, у = 0

 

 

  1. НАЙТИ ОБЩЕЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПЕРВОГО

ПОРЯДКА:

 

 

  1. ВЫЧИСЛИТЬ ВЫБОРОЧНЫЕ СРЕДНЕЕ, ДИСПЕРСИЮ И СРЕДНЕКВАДРАТИЧНОЕ ОТКЛОНЕНИЕ ДЛЯ СЛЕДУЮЩЕЙ ВЫБОРКИ:

 

хί: 3,26; 3,11; 2,64; 3,31; 3,82; 3,85; 3,24; 3,25; 3,12; 2,91; 3,33; 3,43.

ВАРИАНТ № 4

 

  1. ВЫЧИСЛИТЬ ПРЕДЕЛЫ, НЕ ПОЛЬЗУЯСЬ ПРАВИЛОМ ЛОПИТАЛЯ:

а) б)

 

 

  1. ЗАДАНА ФУНКЦИЯ РАЗЛИЧНЫМИ АНАЛИТИЧЕСКИМИ ВЫРАЖЕНИЯМИ ДЛЯ РАЗЛИЧНЫХ ОБЛАСТЕЙ ИЗМЕНЕНИЯ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ. НАЙТИ ТОЧКИ РАЗРЫВА ФУНКЦИИ, ЕСЛИ ОНИ СУЩЕСТВУЮТ. СДЕЛАТЬ ЧЕРТЕЖ.
  5х - 2,   если           х   ≤ -1,    
у = 7 х, если -1 < х ≤ 0,    
  1/х, если     х > 0.    
                     
  1. НАЙТИ ЗНАЧЕНИЕ ПРОИЗВОДНОЙ ФУНКЦИИ , ПРИ х = −2

=

 

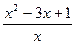
  1. НАЙТИ ЧАСТНЫЕ ПРОИЗВОДНЫЕ 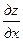; 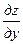ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

 

 

  1. НАЙТИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ:

 

 

  1. ВЫЧИСЛИТЬ ПЛОЩАДЬ ФИГУРЫ, ОГРАНИЧЕННОЙ ЛИНИЯМИ:

у = х2 −2х + 2, х = −1, х = 2 И ОТРЕЗКОМ [−1, 2] ОСИ ОХ.

 

 

  1. НАЙТИ ОБЩЕЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПЕРВОГО

ПОРЯДКА: .

 

 

  1. ВЫЧИСЛИТЬ ВЫБОРОЧНЫЕ СРЕДНЕЕ, ДИСПЕРСИЮ И СРЕДНЕКВАДРАТИЧНОЕ ОТКЛОНЕНИЕ ДЛЯ СЛЕДУЮЩЕЙ ВЫБОРКИ:

 

хί: 1,08; 1,13; 0,94; 0,95; 1,38; 0,76; 1,25; 0,55; 0,88; 1,44; 1,15; 1,12.

 

 

ВАРИАНТ № 5

 

  1. ВЫЧИСЛИТЬ ПРЕДЕЛЫ, НЕ ПОЛЬЗУЯСЬ ПРАВИЛОМ ЛОПИТАЛЯ:

а) б)

 

  1. ЗАДАНА ФУНКЦИЯ РАЗЛИЧНЫМИ АНАЛИТИЧЕСКИМИ ВЫРАЖЕНИЯМИ ДЛЯ РАЗЛИЧНЫХ ОБЛАСТЕЙ ИЗМЕНЕНИЯ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ. НАЙТИ ТОЧКИ РАЗРЫВА ФУНКЦИИ, ЕСЛИ ОНИ СУЩЕСТВУЮТ. СДЕЛАТЬ ЧЕРТЕЖ.

 

  х2, если х ≤ 0,
у = - х, если 0 < х ≤ 2,
  5, если х > 2.

 

  1. НАЙТИ ПРОИЗВОДНУЮ ФУНКЦИИ В ТОЧКЕ х = π/2, .

 

  1. НАЙТИ ЧАСТНЫЕ ПРОИЗВОДНЫЕ 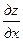; 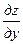ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

z =

 

  1. НАЙТИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ:
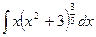
  1. СКОРОСТЬ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ ТЕЛА ЗАДАНА УРАВНЕНИЕМ (м/с). ВЫЧИСЛИТЕ ЕГО ПУТЬ, ПРОЙДЕННЫЙ ОТ НАЧАЛА ДВИЖЕНИЯ ДО ОСТАНОВКИ.

 

  1. НАЙТИ ОБЩЕЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПЕРВОГО

ПОРЯДКА: .

 

  1. ВЫЧИСЛИТЬ ВЫБОРОЧНЫЕ СРЕДНЕЕ, ДИСПЕРСИЮ И СРЕДНЕКВАДРАТИЧНОЕ ОТКЛОНЕНИЕ ДЛЯ СЛЕДУЮЩЕЙ ВЫБОРКИ:

 

хί: 1,05; 1,23; 0,91; 1,44; 0,96; 1,13; 1,14; 1,22; 1,05; 0,88; 0,76;1,14.

 

 

ВАРИАНТ № 6

 

  1. ВЫЧИСЛИТЬ ПРЕДЕЛЫ, НЕ ПОЛЬЗУЯСЬ ПРАВИЛОМ ЛОПИТАЛЯ:

а) б)

 

  1. ЗАДАНА ФУНКЦИЯ РАЗЛИЧНЫМИ АНАЛИТИЧЕСКИМИ ВЫРАЖЕНИЯМИ ДЛЯ РАЗЛИЧНЫХ ОБЛАСТЕЙ ИЗМЕНЕНИЯ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ. НАЙТИ ТОЧКИ РАЗРЫВА ФУНКЦИИ, ЕСЛИ ОНИ СУЩЕСТВУЮТ. СДЕЛАТЬ ЧЕРТЕЖ.
  х + 2,   если           х   < -2,    
у = 0, если -2 ≤ х ≤ 0,    
  2 + х, если     х > 0.    

 

  1. НАЙТИ ЗНАЧЕНИЕ ПРОИЗВОДНОЙ ФУНКЦИИ , ПРИ х = 2

  1. НАЙТИ ЧАСТНЫЕ ПРОИЗВОДНЫЕ 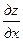; 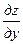ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

z =

 

  1. НАЙТИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ:
  1. ТЕЛО ДВИЖЕТСЯ ПО ПРЯМОЙ СО СКОРОСТЬЮ , ВЫЧИСЛИТЕ ПУТЬ, ПРОЙДЕННЫЙ ТЕЛОМ ЗА 10-УЮ СЕКУНДУ ОТ НАЧАЛА ДВИЖЕНИЯ.

 

  1. НАЙТИ ОБЩЕЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПЕРВОГО

ПОРЯДКА:

 

  1. ВЫЧИСЛИТЬ ВЫБОРОЧНЫЕ СРЕДНЕЕ, ДИСПЕРСИЮ И СРЕДНЕКВАДРАТИЧНОЕ ОТКЛОНЕНИЕ ДЛЯ СЛЕДУЮЩЕЙ ВЫБОРКИ:

 

хί: 10,70; 9,14; 9,76; 10,25; 9,74; 9,25; 10,44; 8,05; 9,21; 9,22; 10,33; 9,15.

ВАРИАНТ № 7

 

  1. ВЫЧИСЛИТЬ ПРЕДЕЛЫ, НЕ ПОЛЬЗУЯСЬ ПРАВИЛОМ ЛОПИТАЛЯ:

а) 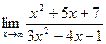б)

 

  1. ЗАДАНА ФУНКЦИЯ РАЗЛИЧНЫМИ АНАЛИТИЧЕСКИМИ ВЫРАЖЕНИЯМИ ДЛЯ РАЗЛИЧНЫХ ОБЛАСТЕЙ ИЗМЕНЕНИЯ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ. НАЙТИ ТОЧКИ РАЗРЫВА ФУНКЦИИ, ЕСЛИ ОНИ СУЩЕСТВУЮТ. СДЕЛАТЬ ЧЕРТЕЖ.

 

  3х +4 , если х <-1,
у = х2 , если -1 ≤ х ≤ 1,
  5, если х > 1.

 

  1. НАЙТИ ЗНАЧЕНИЕ ПРОИЗВОДНОЙ ФУНКЦИИ , ПРИ х = π,

 

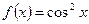
  1. НАЙТИ ЧАСТНЫЕ ПРОИЗВОДНЫЕ 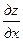; 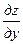ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ .

 

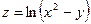  1. НАЙТИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
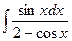
  1. НАЙТИ ПУТЬ, ПРОЙДЕННЫЙ ТЕЛОМ ОТ НАЧАЛА ДВИЖЕНИЯ ДО ОСТАНОВКИ, ЕСЛИ СКОРОСТЬ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ ЗАДАНА УРАВНЕНИЕМ 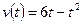(м/с).

 

 

  1. НАЙТИ ОБЩЕЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПЕРВОГО

ПОРЯДКА .

 

  1. ВЫЧИСЛИТЬ ВЫБОРОЧНЫЕ СРЕДНЕЕ, ДИСПЕРСИЮ И СРЕДНЕКВАДРАТИЧНОЕ ОТКЛОНЕНИЕ ДЛЯ СЛЕДУЮЩЕЙ ВЫБОРКИ:

хί: 3,25; 3,12; 2,91; 3,33; 3,43; 3,26; 3,11; 2,64; 3,31; 3,82; 3,85; 3,24.

 

ВАРИАНТ № 8

 

  1. ВЫЧИСЛИТЬ ПРЕДЕЛЫ, НЕ ПОЛЬЗУЯСЬ ПРАВИЛОМ ЛОПИТАЛЯ:

а) б)

 

  1. ЗАДАНА ФУНКЦИЯ РАЗЛИЧНЫМИ АНАЛИТИЧЕСКИМИ ВЫРАЖЕНИЯМИ ДЛЯ РАЗЛИЧНЫХ ОБЛАСТЕЙ ИЗМЕНЕНИЯ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ. НАЙТИ ТОЧКИ РАЗРЫВА ФУНКЦИИ, ЕСЛИ ОНИ СУЩЕСТВУЮТ. СДЕЛАТЬ ЧЕРТЕЖ.
  0,5 (х – 3),   если           х   ≤ -3,    
у = (- 1/3) х2, если -3 < х ≤ 3,    
  х, если     х > 3.    
  1. НАЙТИ ПРОИЗВОДНУЮ ФУНКЦИИ , =

 

  1. НАЙТИ ЧАСТНЫЕ ПРОИЗВОДНЫЕ 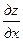; 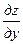ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

z =

 

  1. НАЙТИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ:

 

  1. НАЙТИ ПУТЬ, ПРОЙДЕННЫЙ ТЕЛОМ ЗА 4-УЮ СЕКУНДУ ОТ НАЧАЛА ДВИЖЕНИЯ, ЕСЛИ СКОРОСТЬ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ ЗАДАНА УРАВНЕНИЕМ (м/с).

 

  1. НАЙТИ ОБЩЕЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПЕРВОГО

ПОРЯДКА:

 

  1. ВЫЧИСЛИТЬ ВЫБОРОЧНЫЕ СРЕДНЕЕ, ДИСПЕРСИЮ И СРЕДНЕКВАДРАТИЧНОЕ ОТКЛОНЕНИЕ ДЛЯ СЛЕДУЮЩЕЙ ВЫБОРКИ:

 

хί: 5,12; 3,88; 3,41; 2,88; 3,14; 3,55; 4,12; 3,76; 4,90; 3,75; 2,75; 3,24.

ВАРИАНТ № 9

 

1. ВЫЧИСЛИТЬ ПРЕДЕЛЫ, НЕ ПОЛЬЗУЯСЬ ПРАВИЛОМ ЛОПИТАЛЯ:

а) б)

 

2. ЗАДАНА ФУНКЦИЯ РАЗЛИЧНЫМИ АНАЛИТИЧЕСКИМИ ВЫРАЖЕНИЯМИ ДЛЯ РАЗЛИЧНЫХ ОБЛАСТЕЙ ИЗМЕНЕНИЯ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ. НАЙТИ ТОЧКИ РАЗРЫВА ФУНКЦИИ, ЕСЛИ ОНИ СУЩЕСТВУЮТ. СДЕЛАТЬ ЧЕРТЕЖ.

  х +2, если х ≤ -1,
у = х2, если -1 < х ≤ 3,
  х -5, если х > 3.

3. НАЙТИ ЗНАЧЕНИЕ ПРОИЗВОДНОЙ ФУНКЦИИ , ПРИ ,

 

4. НАЙТИ ЧАСТНЫЕ ПРОИЗВОДНЫЕ 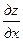; 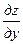ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

 

5. НАЙТИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ:

  1. ТЕЛО ДВИЖЕТСЯ ПО ПРЯМОЙ СО СКОРОСТЬЮ (м/с), ВЫЧИСЛИТЕ ПУТЬ, ПРОЙДЕННЫЙ ТЕЛОМ ОТ НАЧАЛА ДВИЖЕНИЯ ДО ОСТАНОВКИ.

 

 

  1. НАЙТИ ОБЩЕЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПЕРВОГО

ПОРЯДКА: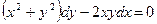

 

 

  1. ВЫЧИСЛИТЬ ВЫБОРОЧНЫЕ СРЕДНЕЕ, ДИСПЕРСИЮ И СРЕДНЕКВАДРАТИЧНОЕ ОТКЛОНЕНИЕ ДЛЯ СЛЕДУЮЩЕЙ ВЫБОРКИ:

 

хί: 1,25; 0,55; 0,88; 1,44; 1,15; 1,12; 1,08; 1,13; 0,94; 0,95; 1,38; 0,76.

ВАРИАНТ № 10

 

  1. ВЫЧИСЛИТЬ ПРЕДЕЛЫ, НЕ ПОЛЬЗУЯСЬ ПРАВИЛОМ ЛОПИТАЛЯ:

а) б)

 

  1. ЗАДАНА ФУНКЦИЯ РАЗЛИЧНЫМИ АНАЛИТИЧЕСКИМИ ВЫРАЖЕНИЯМИ ДЛЯ РАЗЛИЧНЫХ ОБЛАСТЕЙ ИЗМЕНЕНИЯ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ. НАЙТИ ТОЧКИ РАЗРЫВА ФУНКЦИИ, ЕСЛИ ОНИ СУЩЕСТВУЮТ. СДЕЛАТЬ ЧЕРТЕЖ.
  х + 10,   если           х   < -4,    
у = 6, если -4 ≤ х < -2,    
  х2, если     х ≥ -2.    
  1. НАЙТИ ПРОИЗВОДНУЮ ФУНКЦИИ ,

 

  1. НАЙТИ ЧАСТНЫЕ ПРОИЗВОДНЫЕ 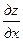; 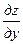ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

 

  1. НАЙТИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ: ∫ х2
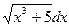
  1. СКОРОСТЬ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ ТЕЛА ЗАДАНА УРАВНЕНИЕМ (м/с). ВЫЧИСЛИТЕ ЕГО ПУТЬ, ПРОЙДЕННЫЙ ОТ НАЧАЛА ДВИЖЕНИЯ ДО ОСТАНОВКИ.

 

 

  1. НАЙТИ ОБЩЕЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПЕРВОГО

ПОРЯДКА:

 

  1. ВЫЧИСЛИТЬ ВЫБОРОЧНЫЕ СРЕДНЕЕ, ДИСПЕРСИЮ И СРЕДНЕКВАДРАТИЧНОЕ ОТКЛОНЕНИЕ ДЛЯ СЛЕДУЮЩЕЙ ВЫБОРКИ:

 

хί: 4,76; 4,78; 4,12; 6,04; 6,26; 3,82; 5,47; 4,46; 5,12; 5,23; 5,21; 5,85.

ВАРИАНТ № 11

 

  1. ВЫЧИСЛИТЬ ПРЕДЕЛЫ, НЕ ПОЛЬЗУЯСЬ ПРАВИЛОМ ЛОПИТАЛЯ:

а) 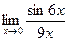б)

 

 

  1. ЗАДАНА ФУНКЦИЯ РАЗЛИЧНЫМИ АНАЛИТИЧЕСКИМИ ВЫРАЖЕНИЯМИ ДЛЯ РАЗЛИЧНЫХ ОБЛАСТЕЙ ИЗМЕНЕНИЯ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ. НАЙТИ ТОЧКИ РАЗРЫВА ФУНКЦИИ, ЕСЛИ ОНИ СУЩЕСТВУЮТ. СДЕЛАТЬ ЧЕРТЕЖ.

 

  -х,   если           х   < 0,    
у = 2 х + 3, если   ≤ х ≤ 3,    
  9, если     х > 3.    

 

  1. НАЙТИ ПРОИЗВОДНУЮ ФУНКЦИИ , .
  1. НАЙТИ ЧАСТНЫЕ ПРОИЗВОДНЫЕ 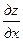; 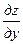ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

z =

 

  1. НАЙТИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ:

  1. НАЙТИ ОБЪЕМ ТЕЛА, ПОЛУЧЕННОГО ВРАЩЕНИЕМ ВОКРУГ ОСИ ОХ ФИГУРЫ, ОГРАНИЧЕННОЙ ЛИНИЯМИ: .
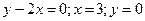  1. НАЙТИ ОБЩЕЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПЕРВОГО

ПОРЯДКА:

  1. ВЫЧИСЛИТЬ ВЫБОРОЧНЫЕ СРЕДНЕЕ, ДИСПЕРСИЮ И СРЕДНЕКВАДРАТИЧНОЕ ОТКЛОНЕНИЕ ДЛЯ СЛЕДУЮЩЕЙ ВЫБОРКИ:

 

хί: 10,44; 8,05; 9,21; 9,22; 10,33; 9,15; 10,70; 9,14; 9,76; 10,25; 9,74; 9,25.

ВАРИАНТ № 12

 

  1. ВЫЧИСЛИТЬ ПРЕДЕЛЫ, НЕ ПОЛЬЗУЯСЬ ПРАВИЛОМ ЛОПИТАЛЯ:

а) 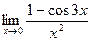б)

  1. ЗАДАНА ФУНКЦИЯ РАЗЛИЧНЫМИ АНАЛИТИЧЕСКИМИ ВЫРАЖЕНИЯМИ ДЛЯ РАЗЛИЧНЫХ ОБЛАСТЕЙ ИЗМЕНЕНИЯ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ. НАЙТИ ТОЧКИ РАЗРЫВА ФУНКЦИИ, ЕСЛИ ОНИ СУЩЕСТВУЮТ. СДЕЛАТЬ ЧЕРТЕЖ.
  3 – х,   если           х   < 0,    
у = х · 3, если   ≤ х ≤ 3,    
  - х, если     х > 3.    

 

  1. НАЙТИ ЗНАЧЕНИЕ ПРОИЗВОДНОЙ ФУНКЦИИ , ПРИ х = π/12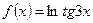

4. НАЙТИ ЧАСТНЫЕ ПРОИЗВОДНЫЕ 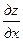; 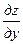ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

z =

 

 

  1. НАЙТИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ:
  1. ВЫЧИСЛИТЬ ПЛОЩАДЬ ФИГУРЫ, ОГРАНИЧЕННОЙ ЛИНИЯМИ: , , ,

 

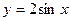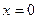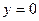
  1. НАЙТИ ОБЩЕЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПЕРВОГО

ПОРЯДКА: 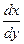– х · у2 = 0;

 

 

  1. ВЫЧИСЛИТЬ ВЫБОРОЧНЫЕ СРЕДНЕЕ, ДИСПЕРСИЮ И СРЕДНЕКВАДРАТИЧНОЕ ОТКЛОНЕНИЕ ДЛЯ СЛЕДУЮЩЕЙ ВЫБОРКИ:

 

хί: 0,88; 1,13; 1,14; 1,22; 1,05;0,76;1,14; 1,05; 1,23; 0,91; 1,44; 0,96.

 

 

ВАРИАНТ № 13

 

  1. ВЫЧИСЛИТЬ ПРЕДЕЛЫ, НЕ ПОЛЬЗУЯСЬ ПРАВИЛОМ ЛОПИТАЛЯ:

а) б)

 

  1. ЗАДАНА ФУНКЦИЯ РАЗЛИЧНЫМИ АНАЛИТИЧЕСКИМИ ВЫРАЖЕНИЯМИ ДЛЯ РАЗЛИЧНЫХ ОБЛАСТЕЙ ИЗМЕНЕНИЯ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ. НАЙТИ ТОЧКИ РАЗРЫВА ФУНКЦИИ, ЕСЛИ ОНИ СУЩЕСТВУЮТ. СДЕЛАТЬ ЧЕРТЕЖ.
  0,5х ,   если           х   ≤ 0,    
у = 1 - х, если   < х < 3,    
  0,   если     х ≥ 3.    

 

  1. НАЙТИ ЗНАЧЕНИЕ ПРОИЗВОДНОЙ ФУНКЦИИ , ПРИ х = 0
  1. НАЙТИ ЧАСТНЫЕ ПРОИЗВОДНЫЕ 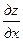; 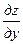ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

 

 

  1. НАЙТИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ:
  1. СКОРОСТЬ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ ТЕЛА ЗАДАНА УРАВНЕНИЕМ (м/с). ВЫЧИСЛИТЕ ЕГО ПУТЬ, ПРОЙДЕННЫЙ ТЕЛОМ ЗА ПЕРВЫЕ 4 С ОТ НАЧАЛА ДВИЖЕНИЯ.

 

 

  1. НАЙТИ ОБЩЕЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПЕРВОГО

ПОРЯДКА:

 

 

  1. ВЫЧИСЛИТЬ ВЫБОРОЧНЫЕ СРЕДНЕЕ, ДИСПЕРСИЮ И СРЕДНЕКВАДРАТИЧНОЕ ОТКЛОНЕНИЕ ДЛЯ СЛЕДУЮЩЕЙ ВЫБОРКИ:

 

хί: 3,24; 2,75; 3,75; 4,90; 3,76; 4,12; 3,55; 3,14; 2,88; 3,41; 3,88; 5,12.

ВАРИАНТ № 14

 

  1. ВЫЧИСЛИТЬ ПРЕДЕЛЫ, НЕ ПОЛЬЗУЯСЬ ПРАВИЛОМ ЛОПИТАЛЯ:

а) б)

 

 

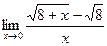
  1. ЗАДАНА ФУНКЦИЯ РАЗЛИЧНЫМИ АНАЛИТИЧЕСКИМИ ВЫРАЖЕНИЯМИ ДЛЯ РАЗЛИЧНЫХ ОБЛАСТЕЙ ИЗМЕНЕНИЯ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ. НАЙТИ ТОЧКИ РАЗРЫВА ФУНКЦИИ, ЕСЛИ ОНИ СУЩЕСТВУЮТ. СДЕЛАТЬ ЧЕРТЕЖ.
  х,   если           х   ≤ -1,    
у = , если -1 < х < 1,    
  -5, если     х ≥ 1.    

 

  1. НАЙТИ ПРОИЗВОДНУЮ ФУНКЦИИ , .

 

  1. НАЙТИ ЧАСТНЫЕ ПРОИЗВОДНЫЕ 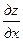; 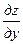ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

 

  1. НАЙТИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ:
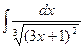
  1. СКОРОСТЬ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ ТЕЛА ЗАДАНА УРАВНЕНИЕМ (м/с). ВЫЧИСЛИТЕ ЕГО ПУТЬ, ПРОЙДЕННЫЙ ОТ НАЧАЛА ДВИЖЕНИЯ ДО ОСТАНОВКИ.

 

 

  1. НАЙТИ ОБЩЕЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПЕРВОГО

ПОРЯДКА: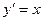

  1. ВЫЧИСЛИТЬ ВЫБОРОЧНЫЕ СРЕДНЕЕ, ДИСПЕРСИЮ И СРЕДНЕКВАДРАТИЧНОЕ ОТКЛОНЕНИЕ ДЛЯ СЛЕДУЮЩЕЙ ВЫБОРКИ:

 

хί: 3,33; 3,43; 3,25; 3,12; 2,91; 3,26; 3,11; 2,64; 3,31; 3,82; 3,85; 3,24.

 

ВАРИАНТ № 15

 

  1. ВЫЧИСЛИТЬ ПРЕДЕЛЫ, НЕ ПОЛЬЗУЯСЬ ПРАВИЛОМ ЛОПИТАЛЯ:

а) б)

 

 

  1. ЗАДАНА ФУНКЦИЯ РАЗЛИЧНЫМИ АНАЛИТИЧЕСКИМИ ВЫРАЖЕНИЯМИ ДЛЯ РАЗЛИЧНЫХ ОБЛАСТЕЙ ИЗМЕНЕНИЯ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ. НАЙТИ ТОЧКИ РАЗРЫВА ФУНКЦИИ, ЕСЛИ ОНИ СУЩЕСТВУЮТ. СДЕЛАТЬ ЧЕРТЕЖ.
  3х – 4,   если           х   < -1,    
у = х2, если -1 ≤ х ≤ 1,    
  -1, если     х > 1.    

 

  1. НАЙТИ ЗНАЧЕНИЕ ПРОИЗВОДНОЙ ФУНКЦИИ , ПРИ ,

 

  1. НАЙТИ ЧАСТНЫЕ ПРОИЗВОДНЫЕ 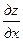; 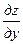ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

z =

 

 

  1. НАЙТИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ:
  1. СКОРОСТЬ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ ТЕЛА ЗАДАНА УРАВНЕНИЕМ 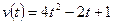(м/с). ВЫЧИСЛИТЕ ЕГО ПУТЬ, ПРОЙДЕННЫЙ ТЕЛОМ ЗА ПЕРВЫЕ 3 С ОТ НАЧАЛА ДВИЖЕНИЯ.

 

 

  1. НАЙТИ ОБЩЕЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПЕРВОГО

ПОРЯДКА:

 

  1. ВЫЧИСЛИТЬ ВЫБОРОЧНЫЕ СРЕДНЕЕ, ДИСПЕРСИЮ И СРЕДНЕКВАДРАТИЧНОЕ ОТКЛОНЕНИЕ ДЛЯ СЛЕДУЮЩЕЙ ВЫБОРКИ:

 

хί: 1,05; 1,23; 0,91; 1,44; 0,96; 1,13; 1,14; 1,22; 1,05; 0,88; 0,76;1,14.

 

 

ВАРИАНТ № 16

 

  1. ВЫЧИСЛИТЬ ПРЕДЕЛЫ, НЕ ПОЛЬЗУЯСЬ ПРАВИЛОМ ЛОПИТАЛЯ:

а) 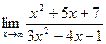б)

 

 

  1. ЗАДАНА ФУНКЦИЯ РАЗЛИЧНЫМИ АНАЛИТИЧЕСКИМИ ВЫРАЖЕНИЯМИ ДЛЯ РАЗЛИЧНЫХ ОБЛАСТЕЙ ИЗМЕНЕНИЯ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ. НАЙТИ ТОЧКИ РАЗРЫВА ФУНКЦИИ, ЕСЛИ ОНИ СУЩЕСТВУЮТ. СДЕЛАТЬ ЧЕРТЕЖ.
  х + 2, если х ≤ -1,
у = х2, если -1 < х ≤ 3,
  х - 5, если х > 3.
  1. НАЙТИ ПРОИЗВОДНУЮ ФУНКЦИИ , .

 

  1. НАЙТИ ЧАСТНЫЕ ПРОИЗВОДНЫЕ 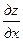; 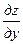ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

 

 

  1. НАЙТИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ:
  1. НАЙТИ ПУТЬ, ПРОЙДЕННЫЙ ТЕЛОМ ЗА ПЕРВЫЕ 5 С ОТ НАЧАЛА ДВИЖЕНИЯ, ЕСЛИ СКОРОСТЬ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ ЗАДАНА УРАВНЕНИЕМ (м/с)..

 

 

  1. НАЙТИ ОБЩЕЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПЕРВОГО

ПОРЯДКА:

 

  1. ВЫЧИСЛИТЬ ВЫБОРОЧНЫЕ СРЕДНЕЕ, ДИСПЕРСИЮ И СРЕДНЕКВАДРАТИЧНОЕ ОТКЛОНЕНИЕ ДЛЯ СЛЕДУЮЩЕЙ ВЫБОРКИ:

 

хί: 3,26; 3,11; 2,64; 3,31; 3,82; 3,85; 3,24; 3,25; 3,12; 2,91; 3,33; 3,43.

 

 

ВАРИАНТ № 17

 

  1. ВЫЧИСЛИТЬ ПРЕДЕЛЫ, НЕ ПОЛЬЗУЯСЬ ПРАВИЛОМ ЛОПИТАЛЯ:

а) б)

 

  1. ЗАДАНА ФУНКЦИЯ РАЗЛИЧНЫМИ АНАЛИТИЧЕСКИМИ ВЫРАЖЕНИЯМИ ДЛЯ РАЗЛИЧНЫХ ОБЛАСТЕЙ ИЗМЕНЕНИЯ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ. НАЙТИ ТОЧКИ РАЗРЫВА ФУНКЦИИ, ЕСЛИ ОНИ СУЩЕСТВУЮТ. СДЕЛАТЬ ЧЕРТЕЖ.
  -х,   если           х   < 0,    
у = 2 х + 3, если   ≤ х ≤ 3,    
  9, если     х > 3.    

 

  1. НАЙТИ ЗНАЧЕНИЕ ПРОИЗВОДНОЙ ФУНКЦИИ , ПРИ х = 0

 

  1. НАЙТИ ЧАСТНЫЕ ПРОИЗВОДНЫЕ 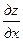; 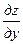ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

 

 

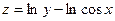
  1. НАЙТИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ:
  1. ВЫЧИСЛИТЬ ПЛОЩАДЬ ФИГУРЫ, ОГРАНИЧЕННОЙ ЛИНИЯМИ: у2 = 9х, х = 16, х = 25, у = 0

 

 

  1. НАЙТИ ОБЩЕЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПЕРВОГО

ПОРЯДКА: .

 

 

  1. ВЫЧИСЛИТЬ ВЫБОРОЧНЫЕ СРЕДНЕЕ, ДИСПЕРСИЮ И СРЕДНЕКВАДРАТИЧНОЕ ОТКЛОНЕНИЕ ДЛЯ СЛЕДУЮЩЕЙ ВЫБОРКИ:

 

хί: 9,76; 10,25; 9,15; 10,70; 9,14; 9,74; 9,25; 10,44; 8,05; 9,21; 9,22; 10,33.

ВАРИАНТ № 18

 

  1. ВЫЧИСЛИТЬ ПРЕДЕЛЫ, НЕ ПОЛЬЗУЯСЬ ПРАВИЛОМ ЛОПИТАЛЯ:

а) 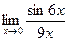б)

 

  1. ЗАДАНА ФУНКЦИЯ РАЗЛИЧНЫМИ АНАЛИТИЧЕСКИМИ ВЫРАЖЕНИЯМИ ДЛЯ РАЗЛИЧНЫХ ОБЛАСТЕЙ ИЗМЕНЕНИЯ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ. НАЙТИ ТОЧКИ РАЗРЫВА ФУНКЦИИ, ЕСЛИ ОНИ СУЩЕСТВУЮТ. СДЕЛАТЬ ЧЕРТЕЖ.
  0,5х ,   если           х   ≤ 0,    
у = 1 - х, если   < х ≤ 3,    
  5,   если     х > 3.    

 

3. НАЙТИ ЗНАЧЕНИЕ ПРОИЗВОДНОЙ ФУНКЦИИ , ПРИ х = 5, =

 

  1. НАЙТИ ЧАСТНЫЕ ПРОИЗВОДНЫЕ 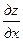; 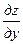ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

z =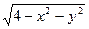

 

5. НАЙТИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ:

  1. ВЫЧИСЛИТЬ ПЛОЩАДЬ ФИГУРЫ, ОГРАНИЧЕННОЙ ЛИНИЯМИ:

у = х2 − 2х + 2, х = −1, х = 2, у = 0

 

 

  1. НАЙТИ ОБЩЕЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПЕРВОГО

ПОРЯДКА:

 

  1. ВЫЧИСЛИТЬ ВЫБОРОЧНЫЕ СРЕДНЕЕ, ДИСПЕРСИЮ И СРЕДНЕКВАДРАТИЧНОЕ ОТКЛОНЕНИЕ ДЛЯ СЛЕДУЮЩЕЙ ВЫБОРКИ:

 

хί: 3,76; 4,90; 5,12; 3,88; 3,41; 2,88; 3,14; 3,55; 4,12; 3,75; 2,75; 3,24.

ВАРИАНТ № 19

 

  1. ВЫЧИСЛИТЬ ПРЕДЕЛЫ, НЕ ПОЛЬЗУЯСЬ ПРАВИЛОМ ЛОПИТАЛЯ:

а) б)

 

  1. ЗАДАНА ФУНКЦИЯ РАЗЛИЧНЫМИ АНАЛИТИЧЕСКИМИ ВЫРАЖЕНИЯМИ ДЛЯ РАЗЛИЧНЫХ ОБЛАСТЕЙ ИЗМЕНЕНИЯ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ. НАЙТИ ТОЧКИ РАЗРЫВА ФУНКЦИИ, ЕСЛИ ОНИ СУЩЕСТВУЮТ. СДЕЛАТЬ ЧЕРТЕЖ.
  х - 3 ,   если           х   ≤ 1,    
у = х2 + 1, если   < х ≤ 4,    
  17, если     х > 4.    
  1. НАЙТИ ПРОИЗВОДНУЮ ФУНКЦИИ В ТОЧКЕ х = − 1

=

  1. НАЙТИ ЧАСТНЫЕ ПРОИЗВОДНЫЕ 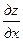; 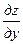ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

 

 

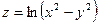
  1. НАЙТИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ:

 

  1. ТЕЛО ДВИЖЕТСЯ ПО ПРЯМОЙ СО СКОРОСТЬЮ , ВЫЧИСЛИТЕ ПУТЬ, ПРОЙДЕННЫЙ ТЕЛОМ ЗА 10-УЮ СЕКУНДУ ОТ НАЧАЛА ДВИЖЕНИЯ.

 

  1. НАЙТИ ОБЩЕЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬН
    Поделиться:





    Воспользуйтесь поиском по сайту:



©2015 - 2024 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...