 |
Математические методы исследования экономики
|
|
|
|
Билет № 13
1) Привести свойства скалярного произведения векторов.
2) Дать понятие опорного плана в задаче линейного программирования.
3) В игре двух лиц с нулевой суммой привести величину среднего выигрыша Игрока 1, если Н – матрица выигрышей, х, у – смешанные стратегии Игроков 1 и 2.
4) Градиент и необходимые условия экстремума функции двух переменных.
5) Привести связь задачи выпуклого программирования и функции Лагранжа.
6) В игре двух лиц с нулевой суммой привести пример чистой стратегии Игрока 2, если матрица выигрышей Н равна
Н = 
7) Для функции f(x,y) = 10х + 15у описать и построить линию уровня:
30х + 15у = 210.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ
Билет № 14
1) Привести правило определения размерности матрицы, являющейся произведением матриц А и В.
2) Сформулировать условие, связанное с тем, что на оптимальном плане некоторое ограничение прямой задачи линейного программирования, например i-ое, выполняется как строгое неравенство.
3) Понятие глобального максимума функции двух переменных.
4) Линейная функция двух переменных и ее график.
5) Привести необходимые и достаточные условия существования седловой точки для функции L(x,y), вогнутой по переменной х и выпуклой по переменной у (L(x,y) - функция двух переменных).
6) Для векторов х = (3, 7, 0, 2), у = (4, -2, 1, 3) построить 2х-3у.
7) Указать область определения функции: f(x,y) = 10 x1/4 y3/4
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ
Билет № 15
|
|
|
1) Привести решение системы линейных уравнений методом Гаусса.
2) Сформулировать условие, связанное со строгой положительностью некоторой координаты, например уi*, оптимального решения двойственной задачи линейного программирования.
3) Что является предметом теории игр?
4) Относительное приращение функции двух переменных по переменной х.
5) Дать определение множителей Лагранжа.
6) Найти произведение матриц А =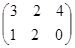 
и В =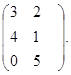 
7) Вычислить значение функции f (x1, x2, x3, x4) = 8 x1 x2 + 4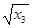 
+ 10 x1 (x4)2 в точке (1, 2, 4, 3)
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ
Билет № 16
1) Объяснить связь базиса и размерности пространства.
2) Дать основные положения задачи линейного программирования.
3) В игре двух лиц с нулевой суммой дать понятие оптимальной стратегии Игрока 1.
4) Дать понятие стационарной точки функции двух переменных.
5) Дать геометрическую интерпретацию метода наискорейшего спуска в случае максимизации функции двух переменных.
6) Для матрицы А =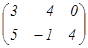 
найти транспонированную и указать ее размерность.
7) Найти частную производную первого порядка по у функции
f(x,y) =20xy.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ
Билет № 17
1) Привести способ вычисления определителя путем разложения его по строке.
2) Привести двойственную задачу для следующей задачи линейного программирования:
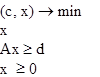
Каковы размерности двойственной задачи линейного программирования, если прямая задача имеет размерности: векторы х и р размерности n, вектор в – размерности m, матрица А – размерности m х n?
3) В игре двух лиц с нулевой суммой привести понятие нижней цены игры.
4) Относительное приращение функции двух переменных по переменной у.
|
|
|
5) Описать метод наискорейшего спуска.
6) Решить систему неравенств
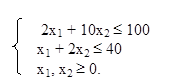
7) Для функции f (x,y) = (x - 3)2 + (y - 4)2 в точке (5,4) построить градиент и линию уровня, проходящую через эту точку. Решение изобразить геометрически.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
|
|
|
