Прогнозирование эффективности инвестиционной деятельности

Методы расчета эффективности долгосрочных инвестиций, основанные на учетной и дисконтированной величине денежных потоков.

При принятии решений в бизнесе о долгосрочных инвестициях возникает потребность в прогнозировании их эффективности. Для этого нужен долгосрочный анализ доходов и издержек.

Основными методами оценки программы инвестиционной деятельности являются:

а) расчет срока окупаемости инвестиций (t);

б) расчет индекса рентабельности инвестиций (IR),

в) определение чистого приведенного эффекта (NPV),

г) определение внутренней нормы доходности (IRR),

д) расчет средневзвешенного срока жизненного цикла инвестиционного проекта, т.е. дюрации (D).

В основу этих методов положено сравнение объема предполагаемых инвестиций и будущих денежных поступлений. Первые два могут базироваться как на учетной величине денежных поступлений, так и на дисконтированных доходах с учетом временной компоненты денежных потоков.

Первый метод оценки эффективности инвестиционных проектов заключается в определении срока, необходимого для того, чтобы инвестиции окупили себя. Он является наиболее простым и по этой причине наиболее распространенным.

Если доходы от проекта распределяются равномерно по годам (проект Б), то срок окупаемости инвестиций определяется делением суммы инвестиционных затрат на величину годового дохода:

t_Б =1000 ∕ 250 = 4 года.

При неравномерном поступлении доходов (проект А) срок окупаемости определяют прямым подсчетом числа лет, в течение которых доходы возместят инвестиционные затраты в проект, т.е. доходы сравняются с расходами.

Пример 1.

	Проект А	Проект Б
Стоимость, тыс. руб.
Прибыль, тыс. руб.:
первый год
второй год
третий год
четвертый год
пятый год
шестой год	—
Всего

Проекты А и Б требуют инвестиций по 1000 тыс. руб. каждый. Проект А обеспечивает прибыль 500 тыс. руб. в течение первых двух лет, после чего доходы резко снижаются. От проекта Б доходы поступают равномерно по 250 тыс. руб. на протяжении шести лет. Из этого следует, что инвестиции в первый проект окупятся за два года, а во второй - за четыре года. Исходя из окупаемости, первый проект более выгодный, чем второй.

Следует заметить при этом, что срок окупаемости инвестиций может быть использован только как вспомогательный показатель. Недостатком данного метода является то, что он не учитывает разницу в доходах по проектам, получаемых после периода окупаемости. Если исходить только из срока окупаемости инвестиций, то нужно инвестировать проект А Однако здесь не учитывается то, что проект Б обеспечивает значительно большую сумму прибыли. Следовательно, оценивая эффективность инвестиций, надо принимать во внимание не только сроки их окупаемости, но и доход на вложенный капитал, для чего рассчитывается индекс рентабельности (IR) и уровень рентабельности инвестиций (R):

.

.

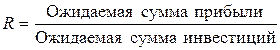Из нашего примера видно, что необходимо вложить средства в проект Б, так как для проекта А

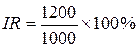= 120%,

а для проекта Б

= 150%,

Однако и этот показатель, рассчитанный на основании учетной величины доходов, имеет свои недостатки: он не учитывает распределения притока и оттока денежных средств по годам и временную стоимость денег. В рассматриваемом примере денежные поступления на четвертом году имеют такой же вес, как и на первом. Обычно же руководство предприятия отдает предпочтение более высоким денежным доходам в первые годы. Поэтому оно может выбрать проект А, несмотря на его более низкую норму прибыли. Сегодняшние деньги всегда дороже будущих, и не только по причине инфляции. Если инвестор получит доход сегодня, то он может пустить их в оборот, к примеру, положить в банк на депозит, и заработать определенную сумму в виде банковского процента. Если же этот доход он получит через несколько лет, то он теряет такую возможность.

Поэтому более научно обоснованной является оценка эффективности инвестиций, основанная на методах наращения (компаундирования) или дисконтирования денежных поступлений, учитывающих изменение стоимости денег во времени, неравноценность современных и будущих благ.

Сущность метода компаундирования состоит в определении суммы денег, которую будет иметь инвестор в конце операции. При использовании этого метода исследование денежного потока ведется от настоящего к будущему. Заданными величинами здесь являются исходная сумма инвестиций, срок и процентная ставка доходности, а искомой величиной -сумма средств, которая будет получена после завершения операции.

Пример 2. Если бы нам нужно было вложить в банк на три года 1000 тыс. руб., который выплачивает 20% годовых, то мы рассчитали бы следующие показатели доходности: за первый год 1000 (1 + 20%) = 1000 × 1,2 = 1200 тыс. руб.; за второй год 1200 (1 + 20%) = 1200 × 1,2 = 1440 тыс. руб.; за третий год 1440 (1 + 20%) = 1440 × 1,2 = 1728 тыс. руб.

Это можно записать и таким образом:

1000 × 1,2 × 1,2 × 1,2 = 1000 × 1,2³ = 1728 тыс. руб.

Из данного примера видно, что 1000 руб. сегодня равноценна 1728 руб. через три года. Напротив, 1728 руб. дохода через три года эквивалентны 1000 руб. на сегодняшний день при ставке рефинансирования 20%.

Пример 2 показывает методику определения стоимости инвестиций при использовании сложных процентов. Сумма годовых процентов каждый год возрастает, поэтому имеем доход, как с первоначального капитала, так и с процентов, полученных за предыдущие годы.

Поэтому для определения стоимости, которую будут иметь инвестиции через несколько лет, при использовании сложных процентов применяют формулу

FV = РV × (1 + r) ⁿ,

где FV - будущая стоимость инвестиций через п лет;

PV - первоначальная сумма инвестиций;

r - ставка процентов в виде десятичной дроби;

п - число лет в расчетном периоде.

При начислении процентов по простой ставке используется следующая формула: FV = РV (1+ rп) = 1000 × (1 + 0,2 × 3) = 1600 тыс. руб.

Если проценты по инвестициям начисляются несколько раз в году по ставке сложных процентов, то формула для определения будущей стоимости вклада имеет следующий вид:

FV = РV (1 + r ∕ m) ^{n m},

где т- число периодов начисления процентов в году.

Допустим, что в вышеприведенном примере проценты начисляются ежеквартально (т = 4, п = 3). Тогда будущая стоимость вклада через три года составит:

FV = 1000 × (1 + 0,2 ∕ 4)¹² = 100 × 1,79585 = 1795,85 тыс. руб.

Часто возникает необходимость сравнения условий финансовых операций, предусматривающих различные периоды начисления процентов. В этом случае осуществляется приведение соответствующих процентных ставок к их годовому эквиваленту по следующей формуле:

ЕFR = (1 + r ∕ m) ^m −1,

где EFR - эффективная ставка процента (ставка сравнения),

т- число периодов начисления; r - ставка процента.

В нашем примере ЕFR = (1 +0,2 ∕ 4)⁴ – 1 = 0,2155 (21,55%).

Если известны величины FV, PV и п, то можно определить процентную ставку по формуле

.

Длительность операции можно определить, зная FV, РV и r, путем логарифмирования:

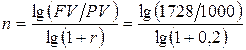= 3 года.

Метод дисконтирования денежных поступлений (ДДП)— исследование денежного потока наоборот — от будущего к текущему моменту времени. Он позволяет привести будущие денежные поступления к сегодняшним условиям. Для этого применяется следующая формула:

,

где k_d - коэффициент дисконтирования.

Если начисление процентов осуществляется т раз в год, то для расчета текущей стоимости будущих доходов используется формула

Иначе говоря, ДДП используется для определения суммы инвестиций, которые необходимо вложить сейчас, чтобы довести их стоимость до требуемой величины при заданной ставке процента.

Для того чтобы через три года стоимость инвестиций составила 1728 тыс. руб. при ставке 20%, необходимо вложить следующую сумму:

РV = 1728 × 1 ∕ l,2³ = 1728 × 0,5787 = 1000 тыс. руб.

Пример 3. Предприятие рассматривает вопрос о том, стоит ли вкладывать 150 тыс. руб. в проект, который через два года принесет доход 200 тыс. руб. Принято решение вложить деньги только при условии, что годовой доход от этой инвестиции составит не менее 10 %, который можно получить, положив деньги в банк. Для того чтобы через два года получить 200 тыс. руб., компания сейчас должна вложить под 10% годовых 165 тыс. руб. (200 х 1 ∕ 1,1²). Проект дает доход в 200 тыс. руб. при меньшей сумме инвестиций (150 тыс. руб.). Это значит, что ставка дохода превышает 10%. Следовательно, проект является выгодным.

ДДП положено в основу методов определения чистой (приведенной) текущей стоимости проектов, уровня их рентабельности, внутренней нормы доходности, дюрации и других показателей.

Метод чистой текущей стоимости (NPV)состоит в следующем.

1. Определяется текущая стоимость затрат (I ₀), т.е. решается вопрос, сколько инвестиций нужно зарезервировать для проекта.

2. Рассчитывается текущая стоимость будущих денежных поступлений от проекта, для чего доходы за каждый год CF (кеш-флоу) приводятся к текущей дате.

Результаты расчетов показывают, сколько средств нужно было бы вложить сейчас для получения запланированных доходов, если бы ставка доходов была равна ставке процента в банке или дивидендной отдаче капитала. Подытожив текущую стоимость доходов за все годы, получим общую текущую стоимость доходов от проекта (PV):

PV = .

3. Текущая стоимость инвестиционных затрат (I ₀) сравнивается с текущей стоимостью доходов (PV). Разность между ними составляет чистую текущую стоимость доходов (NРV):

NРV = PV – I ₀ = – I _0.

NPV показывает чистые доходы или чистые убытки инвестора от помещения денег в проект по сравнению с хранением денег в банке. Если NРV> 0, значит, проект принесет больший доход, чем при альтернативном размещении капитала. Если же NРV < 0, то проект имеет доходность ниже рыночной, и поэтому деньги выгоднее оставить в банке. Проект ни прибыльный, ни убыточный, если NРV = 0.

Пример 4. Предположим, что предприятие рассматривает вопрос о целесообразности вложения 3600 тыс. руб. в проект, который может дать прибыль в первый год 2000 тыс. руб., во второй - 1600 и в третий год - 1200 тыс. руб. При альтернативном вложении капитала ежегодный доход составит 10%. Стоит ли вкладывать средства в этот проект? Чтобы ответить на поставленный вопрос, рассчитаем NPV с помощью дисконтирования денежных поступлений.

Сначала определим текущую стоимость 1 руб. при r = 10%.

Год	1-й	2-й	3-й
(1 + r) n	0,909	0,826	0,751

Затем рассчитаем текущую стоимость доходов.

Год	Денежные поступления, тыс. руб.	Коэффициент дисконтирования	Текущая стоимость доходов, тыс. руб.
	(3600)	1,0 0,909 0,826 0,751	(3600) 1321,6 901,2
		Итого 4040,8

Чистая текущая стоимость денежных поступлений составляет:

NPV = 4040,8 - 3600 = 440,8 тыс. руб.

В нашем примере она больше нуля. Следовательно, доходность проекта выше 10%. Для получения запланированной прибыли нужно было бы вложить в банк 4040 тыс. руб. Поскольку проект обеспечивает такую доходность при затратах 3600 тыс. руб., то он выгоден, так как позволяет получить доходность большую, чем 10 %.

В случаях когда деньги в проект инвестируются не разово, а частями на протяжении нескольких лет, то для расчета NPV применяется следующая формула:

NPV = = – I _0.

где п - число периодов получения доходов;

j - число периодов инвестирования средств в проект.

Рассмотрим данную ситуацию на примере 1 (табл. 23.4). Первый объект строится в течение двух лет и начинает приносить доход с третьего года. Второй проект требует разового вложения капитала и с первого же года начинает приносить прибыль. Альтернативная ставка доходности, доступная данному предприятию, принимаемая в качестве дисконта, равна 10%.

Если сопоставить дисконтированный доход с дисконтированной суммой инвестиционных затрат, то можно убедиться в преимуществе второго проекта.

NРV_А = 833 − 867,2 = -34,2;

NРV_Б = 1088,75 − 1000 = +88,75.

Таблица 23.4

Расчет текущей стоимости доходов и инвестиционных затрат

Показатель	Учетная стоимость затрат и доходов, тыс. руб.	Коэффициент дисконтирования r = 0,10	Дисконтированная сумма затрат, тыс. руб.
Проект А	Проект Б	Проект А	Проект Б
Инвестиционные затраты, тыс. руб.				867,2
В том числе:
первый год		—	0,909	454,5	—
второй год		—	0,826	413,0	—
Доход, тыс. руб.:
первый год	—		0,909	—	227,25
второй год	—		0,826	—	206,50
третий год			0,751	375,5	187,75
четвертый год			0,683	341,5	170,75
пятый год			0,621	62,1	155,25
шестой год			0,565	28,3	141,25
седьмой год		—	0,513	25,6	—
Итого дохода			—	833,0	1088,75

Важной проблемой при прогнозировании эффективности инвестиционных проектов является рост цен в связи с инфляцией. В условиях инфляции для дисконтирования денежных потоков нужно применять не реальную, а номинальную ставку доходности. Чтобы понять методику учета инфляции, необходимо выяснить разницу между реальной и номинальной ставкой дохода.

Зависимость между реальной и номинальной ставкой дохода можно выразить следующим образом:

(1 + r)(l + m) = 1 + d, d = (1 + r)(l + т) – 1,

где r - необходимая реальная ставка дохода (до поправки на инфляцию);

т - темп инфляции, который обычно измеряется индексом розничных цен;

d - необходимая денежная ставка дохода.

Предположим, инвестор имеет 1 млн. руб., который он желает вложить так, чтобы ежегодно его состояние увеличивалось на 20%. Допустим, что темп инфляции 50% в год. Если инвестор желает получить реальный доход 20% на свой капитал, то он обязан защитить свои деньги от инфляции

Денежная (номинальная) ставка дохода, которая нужна инвестору для получения реального дохода в 20% и защиты от инфляции в 50%, составит:

d = (1 + 0,2) × (1 + 0,5) – 1= 0,8, или 80%.

Зная номинальную (денежную) ставку доходности, можно определить реальную ставку по следующей формуле:

; или 20%.

Если затраты и цены растут одинаковыми темпами в соответствии с индексом инфляции, то в методах ДДП можно не учитывать инфляцию. Ситуация изменяется, если затраты и цены растут разными темпами. Тогда нельзя производить дисконтирование денежных поступлений, выраженных в постоянных ценах по реальной ставке дохода. Правильный метод - расчет фактических денежных поступлений с учетом роста цен и дисконтирования их по денежной ставке дохода.

Пример 5. Предприятие решает, следует ли ему вкладывать средства в оборудование, стоимость которого 3,5 млн. руб. Это позволяет увеличить объем продаж на 6 млн. руб. (в постоянных ценах) на протяжении двух лет. Затраты составят 3 млн. руб. Реальная ставка дохода - 10%, темп инфляции - 50% в год. В случае реализации проекта цены на продукцию будут расти всего на 30%, а затраты - на 50% в год.

Определим сначала необходимую денежную ставку дохода:

(1,10 × 1,5) – 1 = 0,65, или 65 %,

а также выручку, затраты и доход.

1-й год	Реализация	6 млн. руб. × 1,3 = 7,8 млн. руб.
	Затраты	3 млн. руб. × 1,5 = 4,5 млн. руб.
	Доход	7,8 – 4,5 = 3,3 млн. руб.
2-й год	Реализация	6 млн. руб. × 1,3 × 1,3 = 10,14млн. руб.
	Затраты	3 млн. руб. × 1,5 × 1,5 = 6,75 млн. руб.
	Доход	10,14 – 6,75 = 3,39 млн. руб.

Рассчитаем текущую стоимость доходов.

Год	Денежные поступления, млн. руб.	Коэффициент дисконтирования при r = 0,65	Текущая стоимость доходов, млн. руб.
	(3,5)	1,0	(3,5)
	3,3	0,606	2,00
	3,39	0,367	1,24
Итого 3,24

Чистая текущая стоимость составляет 3,24 – 3,5 = -0,26 млн. руб. Результат отрицательный, следовательно, проект невыгодный для предприятия.

Если бы мы в этом случае применили реальную ставку дохода 10% к денежным поступлениям в текущих ценах, то допустили бы ошибку.

Год	Денежные поступления, млн. руб.	Коэффициент дисконтирования при r = 0,1	Текущая стоимость доходов, млн. руб.
	(3,5)	1,0	(3,5)
	3,0	0,909	2,7
	3,0	0,826	2,5
	Итого 5,2

Чистая текущая стоимость доходов в этом случае будет больше нуля и составит 5,2 – 3,5 = +1,7 млн. руб. Это неправильный результат.

Таким образом, с помощью метода чистой текущей стоимости (чистого приведенного эффекта) можно довольно реально оценить доходность проектов. Этот метод используется в качестве основного при анализе эффективности инвестиционной деятельности, хотя это не исключает возможности применения и других методов.

Важным показателем, используемым для оценки и прогнозирования эффективности инвестиций, является индекс рентабельности, основанный на дисконтировании денежных поступлений. Расчет его производится по формуле

.

В отличие от чистой текущей стоимости данный показатель является относительным, поэтому его удобно использовать при выборе варианта проекта инвестирования из ряда альтернативных.

Проект	Инвестиции	Годовой доход в течение пяти лет	PV из расчета 10 % годовых	NPV	Индекс рентабельности
А			568,5	68,5	1,14
В			322,0	22,0	1,07
С			879,0	79,0	1,10

По величине NPV наиболее выгоден проект С, а по уровню индекса рентабельности - проект А.

Очень популярным показателем, который применяется для оценки эффективности инвестиций, является внутренняя норма доходности (IRR). Этота ставка дисконта, при которой дисконтированные доходы от проекта равны инвестиционным затратам. Внутренняя норма доходности определяет максимально приемлемую ставку дисконта, при которой можно инвестировать средства без каких-либо потерь для собственника. Ее значение находят из следующего уравнения:

.

Экономический смысл данного показателя заключается в том, что он показывает ожидаемую норму доходности или максимально допустимый уровень инвестиционных затрат в оцениваемый проект. IRR должен быть выше средневзвешенной цены инвестиционных ресурсов:

IRR > СС.

Если это условие выдерживается, инвестор может принять проект, в противном случае он должен быть отклонен.

Для нахождения IRR можно использовать финансовые функции программы калькуляции электронной таблицы Excel или финансового калькулятора. При отсутствии возможности их использования определить его уровень можно методом последовательной итерации, рассчитывая NРV при различных значениях дисконтной ставки (r) до того значения, пока величина NPV примет отрицательное значение, после чего значение IRR находят по формуле

.

При этом должны соблюдаться следующие неравенства: r_a < IRR < r_b, а NРV_a > 0 > NРV_b .

Пример 6.

Требуется найти значение IRR для проекта стоимостью 5 млн. руб., который будет приносить доход в течение четырех лет по 2 млн. руб. ежегодно.

Возьмем произвольно два значения ставки дисконтирования (r = 20% и r = 25%) и рассчитаем текущую стоимость доходов (табл. 23.5).

Таблица 23.5

Расчет исходных данных для определения IRR

Год	Денежный поток, тыс. руб.	Вариант А (r = 20%)	Вариант В (r = 25%)
Kd	PV	Kd	PV
	-5000	1,000	-5000	1,000	-5000
		0,833		0,800
		0,694		0,640
		0,579		0,512
		0,482		0,410
Итого		—
NPV	—	—	+ 176	—	-276

На основании полученных данных найдем значение IRR для рассматриваемого проекта по приведенной выше формуле:

IRR = 20% + (25% – 20%) × = 21,945%.

Точность вычислений IRR зависит от интервала между r_а и r_b. Чем меньше длина интервала между минимальным и максимальным значением ставки дисконтирования, когда функция меняет знак с «+» на «-», тем точнее величина IRR Рассчитаем уточненное значение IRR при длине интервала равном 1%: r_а = 21,5% и r_b = 22,5%.

Год	Денежный поток, тыс. руб.	Вариант 1 (r = 21,5%)	Вариант 2 (r =22,5%)
Kd	PV	Kd	PV
	-5000	1,000	-5000	1,000	-5000
		0,823		0,816
		0,677		0,666
		0,557		0,544
		0,459		0,444
Итого	—	—		—
NPV	—	—	+32	—	-60

IRR = 21,5% + (22,5% – 21,5%) × = 21,84%.

При такой ставке текущие доходы по проекту будут равны инвестиционным затратам. Чтобы сделать вывод об эффективности проекта, необходимо полученное значение IRR сравнить с требуемым уровнем доходности. Если требуемый уровень доходности для данного проекта составляет 20% годовых, то можно сделать позитивное заключение о выгодности инвестирования в него средств.

Внутреннюю норму доходности можно найти и графическим методом, если рассчитать NРV для всех ставок дисконтирования от нуля до какого-либо разумного большого значения (рис. 23.1). По горизонтальной оси откладывают различные ставки дисконтирования, а по вертикальной оси - соответствующие им значения NРV. График пересечет горизонтальную ось, где NРV= 0, при ставке дисконтирования, которая и является внутренней нормой доходности.

Рис. 23. 1. График NPV инвестиционного проекта

Показатели NPV и IRR взаимно дополняют друг друга. Если NPV измеряет массу полученного дохода, то IRR оценивает способность проекта генерировать доход с каждого рубля инвестиций. Высокое значение NРV неможет быть единственным аргументом при выборе инвестиционного решения, так как оно во многом зависит от масштаба инвестиционного проекта и может быть связано с достаточно высоким риском. Поэтому менеджеры предпочитают относительные показатели, несмотря на достаточно высокую сложность расчетов.

Если имеется несколько альтернативных проектов с одинаковыми значениями NPV, IRR, то при выборе окончательного варианта инвестирования учитывается длительность инвестиций (duration). Дюрацuя (D) - это средневзвешенный срок жизненного цикла инвестиционного проекта, где в качестве весов выступают текущие стоимости денежных потоков, получаемых в период t. Она позволяет привести к единому стандарту самые разнообразные по своим характеристикам проекты (по срокам, количеству платежей в периоде, методам расчета причитающегося процента).

Ключевым моментом этой методики является не то, как долго каждый инвестиционный проект будет приносить доход, а прежде всего то, когда он будет приносить доход и сколько поступлений дохода будет каждый месяц, квартал или год на протяжении всего срока его действия.

Дюрация (средневзвешенный срок погашения) измеряет среднее время жизни инвестиционного проекта или его эффективное время действия. В результате менеджеры получают сведения о том, как долго окупаются для компании инвестиции доходами, приведенными к текущей дате.

Для расчета дюрации (D)используется обычно следующая формула:

,

где РV_t - текущая стоимость доходов за п периодов до окончания срока действия проекта;

t - периоды поступления доходов.

Предположим, что два инвестиционных проекта одинаковой стоимости по 10 млн. руб., рассчитанные на 3 года, приносят одинаковый текущий доход при ставке дисконта 12% годовых. Первый проект имеет единственный денежный поток в конце третьего года в размере 16,86 млн. руб., текущая стоимость которого будет равна 12 млн. руб. (16,86 ∕ 1,12³). Второй проект приносит денежный доход ежегодно по 5 млн. руб. и имеет такую текущую стоимость:

PV (2) = 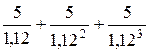= 4,464 + 3,986 + 3,559 = 12 млн. руб.

Однако дюрация для первого проекта будет равна три года, а для второго — 1,93 года.

D (1) = = 3 года.

D (2) = = 1,93 года.

Следовательно, второму проекту следует отдать предпочтение.

Важным моментом при оценке эффективности инвестиционных проектов является анализ чувствительности рассматриваемых критериев на изменение наиболее существенных факторов: уровня процентных ставок, темпов инфляции, расчетного срока жизненного цикла проекта, периодичности получения доходов и т.д. Это позволит определить наиболее рисковые параметры проекта, что имеет значение при обосновании инвестиционного решения.

После принятия инвестиционного решения необходимо спланировать его осуществление и разработать систему послеинвестиционного контроля (мониторинга). Успех проекта желательно оценивать по тем же критериям, которые использовались при его обосновании.

Послеинвестищонный контроль позволяет убедиться, что затраты и техническая характеристика проекта соответствуют первоначальному плану; повысить уверенность в том, что инвестиционное решение было тщательно продумано и обосновано; улучшить оценку последующих инвестиционных проектов.

⇐ Предыдущая38394041424344454647Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: