 |
Дифференциальное исчисление функции одной переменной
|
|
|
|
Пределы
1.1. Среди графиков, приведенных на рис. 1.1, укажите ВСЕ, соответствующие формуле

1.2. Среди графиков, приведенных на рис. 1.1, укажите ВСЕ, соответствующие формуле

1.3. Среди графиков, приведенных на рис. 1.1, укажите ВСЕ, соответствующие формуле

Рис. 1.1
1.4. Укажите ВСЕ утверждения, справедливые для графика функции, изображенного на рис. 1. 2:
Рис. 1.2


1.5. Если 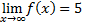 , то
, то  равен
равен
а) 3; б) -3; в) 0; г) ∞; д) не существует.
1.6. Если  , то
, то  равен
равен
а) 3; б) -3; в) 0; г) ∞; д) не существует.
1.7. Если  , то
, то  равен
равен
а) 3; б) -3; в) 0; г) ∞; д) не существует.
1.8. Если  , и
, и  – чётная,то
– чётная,то  равен
равен
а) 3; б) -3; в) 0; г) ∞; д) не существует.
1.9. Вычислить  .
.
а) 1; б) -1; в) 0; г) ∞; д) не существует.
1.10. Вычислить  .
.
а) 1; б) -1; в) 0; г) ∞; д) не существует.
1.11. Вычислить  .
.
а) 1; б) -1; в) 0; г) ∞; д) не существует.
1.12. Дано  . Укажите ВСЕ верные утверждения:
. Укажите ВСЕ верные утверждения:
 – ограничена в окрестности точки
– ограничена в окрестности точки  ;
;
 – бесконечно большая при
– бесконечно большая при  ;
;
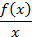
1.12. Дано П т /(*) = 1 ООО ООО ООО. Укажите ВСЕверные утверждения:
^ *->2
а)/ (х) ограничена в окрестности точки х= 2 ;
б) / (х) - бесконечно большая при х —» 2;
| / (х) | |||
| в) —-— —» 500 000 000 при х —> 2; | |||
| г) | бесконечно малая при х —» 2. | ||
| - | |||
| J \х) | |||
| 1.13. | Известно, что при х —>0 а(х) и Р(х) - бесконечно малые и | ||
| а(х) | = | . Какое из следующих утверждений верно при х —> 0? | |
| Hm |
х
а) а(х) и р(х) эквивалентны; б) а(х) более высокого порядка малости, чем Р(х);
в) а(х) более низкого порядка малости, чем Р(х); г) а(х) и р(х) одного порядка малости.
1.14. Известно, что при х —» Хо бесконечно малые а(х)и Р(х) эквива лентны (а(х) ~Р(х)), Какое из следующих утверждений вернопри х —> х0?
|
|
|
а) а(х) более высокого порядка малости, чем Р(х); б) а(х) более низкого порядка малости, чем Р(х); в) а(х) и Р(х) одного порядка малости; г) а(х) и Р(х) нельзя сравнивать.
1.15. Прих —> 1 укажите ВСЕ верные утверждения:
| a) | sin х ~ х; | б) sin(x - 1) ~ (х - 1); | ||||
| в) sin(x + 1) ~ (х + 1); | г) sin(l/x) ~ (1/х). | |||||
| 2 п | ||||||
| 1.16. Вычислить 11тоо((п 2 | п 2 + п 2 | п 2 + " | п 2 ' (П+ " - | |||
| а) | 1; | б) - 1; в) 0; | г) оо; | д) 1/2. |
Непрерывность
2.1. Среди графиков, приведенных на рис. 2.1, укажите ВСЕ, на кото рых функция имеет в точке а разрыв второго рода.
2.2. Среди графиков, приведенных на рис. 2.1, укажите ВСЕ, на кото рых функция имеет в точке а разрыв первого рода.
2.3. Среди графиков, приведенных на рис. 2.1, укажите ВСЕ, на кото рых функция непрерывна в точке а:
| - - | Я | - | л | а. | 7. | |
| ПС | с | X | 6 | |||
| 1) | ||||||
| Рис. 2.1 | ||||||
| 2.4. Известно, что | lim / | (Д = - °°; | Hm | Д х) = 18. Какое из утверждений | ||
| х-> с - 0 | х->с + О |
Верно?
а) с- точка неустранимого разрыва первого рода; б) с- точка устранимого разрыва первого рода; в) с -точка разрыва второго рода; г) с- точка непрерывности.
2.5. Известно, что Нт / (х) = - 5; lim / (х) = - 5; f[c) = - 5. Какое из ут-
х-> с - 0 х->с + О
Верждений верно?
а) с- точка неустранимого разрыва первого рода; б) с- точка устранимого разрыва первого рода; в) с -точка разрыва второго рода; г) с- точка непрерывности.
2.6. Укажите, в каком случае в точке с функция Дх) имеет устранимый разрыв:
| a) | lim /(х) = -5; | lim Д х) = -5;Д С) = 0; |
| х-> с - 0 | х-> с + 0 | |
| б) | lim /(х) = -5; | lim /(х) = 5 ;Дс) = 5; |
| х-> с - 0 | х-> с + 0 | |
| в) | Нт Д х) = - 5; | lim Д х) = -оо; |
| х-> с - 0 | х-> с + 0 | |
| г) | lim Д х) = - 5; | lim Д х) = -5 ;J[c) = - 5. |
| х-> с - 0 | х-> с + 0 | |
| 2.7. | Известно, что f(x) -непрерывная функция. Какое из следующих ут | |
| верждений верно? | ||
| a) | lim (/ (х + Ах) - | / (х)) = 1; б) lim (/(х + Ах) - / (х)) = 0; |
| Дх^-0 | ||
| б) Hm (/ (X +Ах)- Д х)) = оо; г) Нт (Д х + Ах) - /(х)) = -оо. | ||
| ' | Ах—>0 | у Ах—>0 |
|
|
|
| 2.8. | Функция | Дх) | имеет | устранимый разрыв | в | точке х= 2 и | ||||||||
| lim f{x) = l. Тогда | lim | /(х) | равен | |||||||||||
| х —^2—0 | х —^2+О | |||||||||||||
| а) | 1; | б) - 1; | в) | 0; г) оо; | д) другой ответ. | |||||||||
| 2.9. | Известно, | что | Д х) | и | Дх) | - | непрерывны | в | точке х= 1; | |||||
| Д \) Ф 0;Д1) = 0.Укажите ВСЕ функции непрерывные в точке х = 1: | ||||||||||||||
| a)./W +g(x); б) | f(x)J _ f X); | B)./(x)g(x); | г) | Д) 7 ДУ + «(х)' | ||||||||||
| 2.10. Укажите ВСЕ функции непрерывные в точке х = 1: | ||||||||||||||
| a) | . | , | х - 1 | sinx | sinx | , | д) | . | ||||||
| sm (x -l); | б) - —; | в) | г) | 1; | sin | - | ||||||||
| sinx | х - 1 | X | х - 1 | |||||||||||
| 2.11. Укажите, | на каком из данных отрезков уравнение lg(x+2) + x = 0 | |||||||||||||
| имеет действительный корень: | ||||||||||||||
| а) [-1; 0]; | б) [0;1]; | в) | [1; 2 ]; | г) [2; 3]; | ||||||||||
| д) уравнение вообще не имеет действительных решений |
Дифференциальное исчисление функции одной переменной
3.1. Какое из нижеперечисленных предложений определяет производ ную функции (когда приращение аргумента стремится к нулю)?
а) Отношение приращения функции к приращению аргумента; б) Предел отношения функции к приращению аргумента; в) Отношение функции к пределу аргумента; г) Отношение предела функции к аргументу;
д) Предел отношения приращения функции к приращению аргумента.
3.2. Первая производная функции показывает
а) скорость изменения функции; б) направление функции; в) приращение функции;
г) приращение аргумента функции.
3.3. Угловой коэффициент касательной, проведенной к графику функ ции в некоторой точке, равен
а) отношению значения функции к значению аргумента в этой точке; б) значению производной функции в этой точке; в) значению дифференциала функции в этой точке; г) значению функции в этой точке;
д) значению тангенса производной функции в этой точке.
3.4. На рисунке 3.1 изображен график функции у= f (x). Тогда произ
|
|
|
водная / \х) это...
а) ТК/МК; б) NK/MK; b)N K; г) МК/ТК; д) MN/MK; е) MN.
У
X х+Ах х
Рис. 3.1
3.5. На рисунке 3.2 изображен график функции у = fix'). Найдите зна
чение / 7 (1,5).
f(x)
0,5 1,5
Рис. 3.2
3.6. Укажите функции, для которых существует конечная производная
в каждой точке числовой оси:
a)y = lruc; 6)y=|siruc|; в)у = х3; г)у = Зх; д )у= \[х.
3.7. Укажите ВСЕ верные утверждения: если функция дифференцируе ма в некоторой точке, то в этой точке...
а) функция не определена; б) можно провести касательную к графику функции;
в) нельзя провести касательную к графику функции; г) функция непрерывна; д) функция имеет экстремум.
3.8. Дифференциал функции равен
а) отношению приращения функции к приращению аргумента; б) произведению приращения функции на приращение аргумента; в) произведению производной на приращение аргумента;
г) приращению функции; д) приращению аргумента.
3.9. Дифференциал постоянной равен...
а) этой постоянной; б) произведению данной постоянной на величину Ах;
в) бесконечно большой величине; г) нулю; д) невозможно определить.
3.10. На рисунке 3.3 изображен график функции у = f (x). Какой отре зок на этом рисунке соответствует дифференциалу dyl
У
X х+Ах х
Рис. 3.3
а) ТК; 6)NK; в) NT; г) МК; д) MN; е) другой ответ.
3.11. Какое из следующих утверждений верно для любой линейной функции?
а) дифференциал функции равен приращению функции; б) дифференциал функции равен приращению аргумента; в) дифференциал функции - это постоянная величина;
г) дифференциал функции равен производной этой функции.
3.12. Какое из следующих утверждений верно для нелинейной функ
Ции?
а) дифференциал функции равен производной этой функции; б) дифференциал функции равен приращению аргумента; в) дифференциал функции равен части приращения функции; г) дифференциал функции - это постоянная величина.
3.13. Если функция у(х) непрерывна на [а;Ь], дифференцируема на ( а;Ь )
|
|
|
и у{а) =у{Ь), то на( а;Ь )можно найти хотя бы одну точку,в которой
а) функция не определена; б) производная функции не существует;
в) нельзя провести касательную к графику функции; г) производная функции обращается в ноль.
| 3.14. Функция у =х | +х... | |||||
| а) возрастает на (- | оо; 0), убывает на | (0; +оо); | ||||
| б) убывает на (- оо; 0), возрастает на | (0; +оо); | |||||
| в) всюду убывает; | г) всюду возрастает; | |||||
| д) другой ответ. | ||||||
| _ | ~ | |||||
| 3.15. Функция У- | э х убывает на | |||||
| а) (3; +оо); | б) | (0; | 1/3); | в) (- | сю; 0)и(0; +сю); | г) (- оо; +оо); |
| д) нигде; | е) | другой ответ. |
| 3.16. Сколько | точек перегиба имеет функция у =х + 4х? | ||||
| а) ни одной; | б) одну; | в) две; | г) три; | д) больше трех. | |
| 3.17. | Какой из графиков на рисунке 3.4 соответствует функции у=Дх), | ||||
| удовлетворяющей условиям / | '(х) <0; / | "(х) > 0? | |||
а) б) в) г)
Рис. 3.4
3.18. Какому условию удовлетворяет функция, график которой изобра жен на рисунке 3.5?
| a)/ 73с) > 0 и / ”(х) > 0; | б) / 7х) > 0 и / "(х) < 0; |
| b) Г (Х) < 0 и Г '(х) > 0; | т)Г(х) < 0 * f" (x) < 0. |
| У | f(x) |
X
Рис. 3.5
3.19. Укажите точки экстремума непрерывной на всей числовой пря
| мой функции у(х), если у' = (х+ 1)2(х -2): | ||
| а) х = 2 - точка max', | б) х = 2 - | точка мш; |
| в) х = -1 - точка max', | г) х = -1 - | точка мш; |
| д) точек экстремума нет. |
3.20. Укажите точки на (а; b ), в которых функция, изображенная на ри сунке 3.6, не дифференцируема.
3.21. Укажите точки, в которых функция, изображенная на рисунке 3.6, имеет максимум.
3.22. Укажите точки на [а;Ь], в которых функция, изображенная на ри сунке 3.6, принимает наименьшее значение.
3.23. Укажите точки на ( а; b ) в которых производная функции, изобра женной на рисунке 3.6, обращается в ноль.
Рис. 3.6
3.24. Для дифференцируемой функции Дх) из приведенных условий вы берите достаточное условие убывания:
| а) / О) > 0; | б) /'О) < 0; | в) | f"(x) >0; |
| г) /" О) < о; | д) / ' О) = о; | е) | /" О) = о. |
3.25. Для дифференцируемой функции Дх) из приведенных условий вы берите достаточное условие выпуклости (выпуклости вверх):
| a) / О) > 0; | б) /'О) < 0; | в) f"(x) > 0; |
| г) /" О) < 0; | д) f \ x) = 0; | е) f \ x) = 0. |
3.26. Для дифференцируемой функции Дх) из приведенных условий вы берите необходимое условие точки перегиба:
| а)/'(* „) > 0; | б) / '(х 0)< 0; | в) /" (х 0)> 0; | ||
| г) /Ч * о) < 0; | д) /'О о) = 0; | е) /" О о) = о. | ||
| 3.27. Найти/'(-1), еслиДх) =х(х+1)(х+2)-...-(*+Ю). | ||||
| а) 18; | б) -18; | в) 9!; | г) -9!; | д) 0. |
|
|
|


