 |
Геометрические параметры цилиндрических зубчатых колес
|
|
|
|
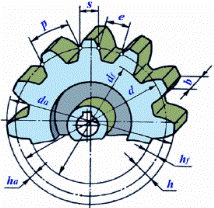
Цилиндрическое зубчатое колесо имеет следующие конструктивные элементы:
1. венец – часть зубчатого колеса, содержащая зубья;
2. ступица с – часть зубчатого колеса, насаживаемая на вал;
3. диск – часть зубчатого колеса между ступицей и венцом.
Контакт пары зубьев цилиндрической прямозубой передачи происходит по линии параллельной оси. При работе прямозубой передачи пара зубьев входит в зацепление сразу по всей длине контакта, что сопровождается ударом зубьев и повышенным шумом, поэтому прямозубые передачи применяют при невысоких окружных скоростях.
d = m∙ z- диаметр делительной окружности;
da =(m∙ z + 2∙m) - диаметр окружности вершин зубьев;
df =(m∙ z – 2,5∙m) - диаметр окружности впадин зубьев;
p = π∙m - шаг по делительной окружности (расстояние между одноименными точками профилей соседних зубьев, измеренное в сечении, нормальном линиям зубьев);
s = 0,5∙p - толщина зуба по делительной окружности;
e = 0,5∙p - ширина впадины по делительной окружности;
ha = m - высота головки зуба;
hf = 1,25∙m - высота ножки зуба;
h = 2,25∙m - высота зуба;
b - ширина зубчатого венца.
р/π =m - окружной модуль зубьев (основная геометрическая характеристика зубьев).
Значения модулей стандартизованы.
Стандартные модули (по ГОСТ 9563-80)
| Ряды | Модуль, мм |
| I | 1; 1,25; 1,5; 2; 2,5;3;4;5;6;8;10;12;16;20;252,5; 3; 4; 5; 6; 8; 10;12; 16; 20; 25 |
| II | 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 5,7; 9; 11; 14; 18; 22 |
Различают индексы, относящиеся: w - к начальной поверхности или окружности; b - к основной поверхности или окружности; а - к поверхности или окружности вершин и головок зубьев;
- к поверхности или окружности впадин и ножек зубьев; t – торцевому сечению; n - нормальному сечению; х - к осевому сечению. Параметрам, относящимся к делительной поверхности или окружности, индекса не присваивают.
|
|
|
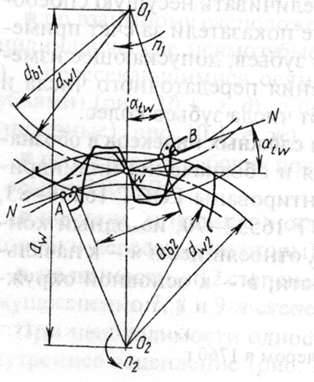
Зубчатое зацепление характеризуется следующими основными параметрами: z1 и z 2 – число зубьев шестерни и колеса; р – делительный окружной шаг зубьев; рb = p∙cos α – основной окружной шаг зубьев; α– угол профиля делительный (равен углу профиля исходного контура, по ГОСТ 13754-81, α= 20°); а = (d1+d2)/2- делительное межосевое расстояние; аw - межосевое расстояние. При отсутствии смещения исходного контура аw= а; α w - угол зацепления или угол профиля начальный определяется из выражения: cos α w = а∙ cos α/ аw; db = d∙cos 
– основной диаметр (диаметр окружности, разверткой которой являются эвольвенты зубьев); dwl и dw2 – начальные диаметры (диаметры окружностей, по которым пара зубчатых колес обкатывается в процессе вращения);
длина активной линии зацепления (l) отсекается окружностями выступов;
коэффициент перекрытия - εα= l /p; передаточное число зацепления: u = ω1/ω2= n1/n2 =d2/d1= z2/z1;
полюс зацепления - точка касания начальных окружностей и одновременно точка пересечения линии центров колес О1O2 с линией зацепления
Цилиндрические передачи с внешним и внутренним зацеплением представлены на рисунке ниже
Линии пересечения боковых поверхностей зубьев с любой круговой цилиндрической поверхностью, соосной с начальной, называют линиями зубьев. Если линии зубьев параллельны оси зубчатого колеса, то его называют прямозубым - а). Если эти линии винтовые постоянного шага, то зубчатое колесо называют косозубым - б). С увеличением угла β наклона зуба повышается нагрузочная способность передачи, но возрастает осевая сила, действующая на валы и опоры. Обычно (β = 8...20°). Разновидность косозубых зубчатых колес – шевронные колеса: без канавки - в) и с канавкой для выхода инструмента - г). Вследствие противоположного направления зубьев на полушевронах осевые силы взаимно уравновешены на колесе и не нагружают опоры. В этом случае угол наклона β = 25... 40°. Для простоты изложения здесь рассматриваются передачи без смещения. Однако в обозначении межосевого расстояния для общности изложения индекс w сохраним.
|
|
|
|
|
|
