 |
Тема №1. Событие. Пространство элементарных событий. Достоверное событие, невозможное событие. Совместные, несовместные события. Равновозможные события. Полная группа событий. Операции над событиями.
|
|
|
|
Событие — это явление, о котором можно сказать, что оно происходит или не происходит, в зависимости от природы самого события.
Под элементарными событиями, связанными с определенным испытанием, понимают все неразложимые результаты этого испытания. Каждое событие, которое может наступить в результате этого испытания, можно рассматривать как некоторое множество элементарных событий.
Пространством элементарных событий называется произвольное множество (конечное или бесконечное). Его элементы — точки (элементарные события). Подмножества пространства элементарных событий называются событиями.
Достоверным событием называется событие, которое вследствие данного испытания обязательно произойдет; (обозначается E).
Невозможным событием называется такое событие, которое вследствие данного испытания не может произойти; (обозначается U). Например, появление одного из шести очков во время одного броска игрального кубика — достоверное событие, а появление 8 очков — невозможное.
Два события называются совместными (совместимыми) в данном опыте, если появление одного из них не исключает появления другого.
Два события называются несовместными (несовместимыми) в данном опыте, если они не могут произойти вместе при одном и том же испытании. Несколько событий называются несовместными, если они попарно несовместны.
| Полная группа событий. Теорема. Сумма вероятностей событий А1, А2,..., Аn, образующих полную группу, равна единице: Р (A1) + Р (А2) +... + Р (Аn) = 1. |
Начало формы
Конец формы
Событие — это явление, о котором можно сказать, что оно происходит или не происходит, в зависимости от природы самого события.
События обозначаются большими буквами латинского алфавита A, B, C,... Любое событие происходит вследствие испытания.
Например, подбрасываем монету — испытание, появление герба — событие; достаем лампу из коробки — испытание, она бракованная — событие; вынимаем наугад шарик из ящика — испытание, шарик оказался черного цвета — событие.
Случайным событием называется событие, которое может произойти или не произойти во время данного испытания. Например, вынимая наугад одну карту из колоды, вы взяли туз; стреляя, стрелок попадает в цель.
Теория вероятности изучает только массовые случайные события.
Достоверным событием называется событие, которое вследствие данного испытания обязательно произойдет; (обозначается E).
Невозможным событием называется такое событие, которое вследствие данного испытания не может произойти; (обозначается U).
Например, появление одного из шести очков во время одного броска игрального кубика — достоверное событие, а появление 8 очков — невозможное.
Равновозможные события — это такие события, каждое из которых не имеет никаких преимуществ в появлении чаще другого во время многочисленных испытаний, которые проводятся с одинаковыми условиями.
Попарно несовместимые события — это события, два из которых не могут произойти вместе.
Вероятность случайного события — это отношение числа событий, которые благоприятствуют этому событию, к общему числу всех равновозможных несовместимых событий:
P(A) =  где A — событие; P(A) — вероятность события; N — общее число равновозможных и несовместимых событий; N(A) — число событий, которые благоприятствуют событию A.
Это — классическое определение вероятности случайного события.
Классическое определение вероятности имеет место для испытаний с конечным числом равновозможных результатов испытания.
Пусть сделано n выстрелов по мишени, из которых оказалось m попаданий. Отношение W(A) =
где A — событие; P(A) — вероятность события; N — общее число равновозможных и несовместимых событий; N(A) — число событий, которые благоприятствуют событию A.
Это — классическое определение вероятности случайного события.
Классическое определение вероятности имеет место для испытаний с конечным числом равновозможных результатов испытания.
Пусть сделано n выстрелов по мишени, из которых оказалось m попаданий. Отношение W(A) =  называется относительной статистической частотой наступления события A.
Следовательно, W(A) — статистическая частота попадания. называется относительной статистической частотой наступления события A.
Следовательно, W(A) — статистическая частота попадания.
Вероятностью события A называется то неизвестное число P, около которого собираются значения статистических частот наступления события A при возрастании числа испытаний. Это — статистическое обозначение вероятности случайного события. |
| Операции над событиями |
Под элементарными событиями, связанными с определенным испытанием, понимают все неразложимые результаты этого испытания. Каждое событие, которое может наступить в результате этого испытания, можно рассматривать как некоторое множество элементарных событий.
Пространством элементарных событий называется произвольное множество (конечное или бесконечное). Его элементы — точки (элементарные события). Подмножества пространства элементарных событий называются событиями.
Все известные отношения и операции над множествами переносятся на события.
Говорят, что событие A является частным случаем события B (или B является результатом A), если множество A является подмножеством B. Обозначают это отношение так же, как для множеств: A ⊂ B или B ⊃ A. Таким образом, отношение A ⊂ B означает, что все элементарные события, входящие в A, входят также в B, то есть при наступлении события A наступает также событие B. При этом, если A ⊂ B и B ⊂ A, то A = B.
Событие A, которое происходит тогда и только тогда, когда событие A не происходит, называется противоположным событию A. Поскольку в каждом испытании происходит одно и только одно из событий — A или A, то P(A) + P(A) = 1, или P(A) = 1 − P(A).
Объединением или суммой событий A и B называется событие C, которое происходит тогда и только тогда, когда или происходит событие A, или происходит событие B, или происходят A и B одновременно. Это обозначается C = A ∪ B или C = A + B.
Объединением событий A1, A2,... An называется событие, которое происходит тогда и только тогда, когда происходит хотя бы одно из данных событий. Обозначается объединение событий A1 ∪ A2 ∪... ∪ An, или  Ak, или A1 + A2 +... + An.
Пересечением или произведением событий A и B называется событие D, которое происходит тогда и только тогда, когда события A и B происходят одновременно, и обозначается D = A ∩ B или D = A × B.
Совмещением или произведением событий A1, A2,... An называется событие, которое происходит тогда и только тогда, когда происходит и событие A1, и событие A2, и т.д., и событие An. Обозначается совмещение так: A1 ∩ A2 ∩... ∩ An или Ak, или A1 + A2 +... + An.
Пересечением или произведением событий A и B называется событие D, которое происходит тогда и только тогда, когда события A и B происходят одновременно, и обозначается D = A ∩ B или D = A × B.
Совмещением или произведением событий A1, A2,... An называется событие, которое происходит тогда и только тогда, когда происходит и событие A1, и событие A2, и т.д., и событие An. Обозначается совмещение так: A1 ∩ A2 ∩... ∩ An или  Ak, или A1 × A2 ×... × An. Ak, или A1 × A2 ×... × An.
|
|
|
|
Тема № 2. Аксиоматическое определение вероятности. Классическое, статистическое, геометрическое определение вероятности события. Свойства вероятности. Теоремы сложения и умножения вероятностей. Независимые события. Условная вероятность. Вероятность наступления хотя бы одного из событий. Формула полной вероятности. Формула Байеса
Численная мера степени объективной возможности наступления события называется вероятностью события. Это определение, качественно отражающее понятие вероятности события, не является математическим. Чтобы оно стало таким, необходимо определить его качественно.
Согласно классическому определению вероятность события А равна отношению числа случаев, благоприятствующих ему, к общему числу случаев, то есть:

Где P(A) – вероятность события А.
 - число случаев благоприятствующих событию А
- число случаев благоприятствующих событию А
 - общее число случаев.
- общее число случаев.
Статистическое определение вероятности:
Статистической вероятностью события А называется относительная частота появления этого события в  произведённых испытаниях, то есть:
произведённых испытаниях, то есть:

Где  - статистическая вероятность события А.
- статистическая вероятность события А.
 - относительная частота(частость) события А.
- относительная частота(частость) события А.
 -число испытаний, в которых появилось события A
-число испытаний, в которых появилось события A
 -общее число испытаний.
-общее число испытаний.
В отличие от «математической» вероятности  , рассматриваемой в классическом определении, статистическая вероятность
, рассматриваемой в классическом определении, статистическая вероятность  является характеристикой опытной, экспериментальной.
является характеристикой опытной, экспериментальной.
|
|
|
Если  есть доля случаев, благоприятствующих событию А, которая определяется непосредственно, без каких-либо испытаний, то
есть доля случаев, благоприятствующих событию А, которая определяется непосредственно, без каких-либо испытаний, то  есть доля тех фактически произведённых испытаний, в которых событие А появилось.
есть доля тех фактически произведённых испытаний, в которых событие А появилось.
Геометрическое определение вероятности:
Геометрической вероятностью события А называется отношение меры области благоприятствующей появлению события А, к мере всех области, то есть:
В одномерном случае:
 |
А С D В
Следует оценить вероятность попадания точки на CD/
Оказывается эта вероятность не зависит от места нахождения CD на отрезке АВ, а зависит лишь от его длины.


2)На области А:
 |
Вероятность попадания точки не зависит ни от форм, ни от месте нахождения В на А, а зависит лишь от площади данного сегмента.

Условная вероятность
Вероятность называется условной, если она вычисляется при определённых условиях и обозначается:

Это вероятность события А. Вычисляется при условии, что событие В уже произошло.
Пример. Производим испытание, извлекаем две карты из колоды: Первая вероятность является безусловной.
Вычисляем вероятность извлечения туза из колоды:

Вычисляем появление 2-тузув из колоды:

А*В – совместное появление событий
 – теорема умножения вероятностей
– теорема умножения вероятностей
Следствие:
Теорема умножения для совместного появления  событий имеет вид:
событий имеет вид:

То есть каждая последующая вероятность вычисляется с тем учётом, что все предыдущие условия уже произошли.
Независимость события:
Независимыми называются 2 события, если появление одного не противоречит появлению другого.

Например, если тузы из колоды извлекаются повторно, тогда они между собой независимы. Повторно, то есть карту посмотрели и вернули обратно в колоду.
Совместные и несовместные события:
Совместными называются 2 события, если появление одного из них не противоречит появлению другого.
Теорема сложения вероятностей совместных событий:
Вероятность появления одного из двух совместных событий равна сумме вероятностей этих событий без их совместного появления.

Для трёх совместных событий:

Несовместными называются события, если никакие два из них не могут появиться одновременно в результате однократного испытания случайного эксперимента.
Теорема: Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий.

Вероятность суммы событий:
Теорема сложения вероятностей:
Вероятность суммы конечного числа несовместных событий равна сумме вероятностей этих событий:
|
|
|

Следствие 1:
Сумма вероятностей событий, образующих полную группу равна единице:


Следствие 2:
Сумма вероятностей противоположных событий равна единице:

Замечание: Следует подчеркнуть, что рассмотренная теорема сложения применима только для несовместных событий.
Вероятность противоположных событий:
Противоположными называются два единственно возможных события, образующих полную группу. Одно из двух противоположных событий обозначено через А, другое – через  .
.
Пример: Попадание и промах при выстреле по цели – противоположные события. Если A – попадание, то  – промах.
– промах.
Теорема: Сумма вероятностей противоположных событий равна единице:

Замечание 1: Если вероятность одного из двух противоположных событий обозначена через p, то вероятность другого события обозначают через q Таким образом, в силу предыдущей теоремы:

Замечание 2: При решении задач на отыскание вероятности события A часто выгодно сначала вычислить вероятность события  , а затем найти искомую вероятность по формуле:
, а затем найти искомую вероятность по формуле:

Вероятность появления хотя бы одного события:
Допустим, что в результате эксперимента может появиться одно, какая-то часть или ни одно событие.
Теорема: Вероятность появления хотя бы одного события из совокупности  независимых событий равна разности между единицей и их вероятностью не появления событий
независимых событий равна разности между единицей и их вероятностью не появления событий  .
.

Формула полной вероятности событий:
Теорема: Если событие F может произойти только при условии появления одного из событий(гипотез)  , образующих полную группу, то вероятность события F равна сумме произведений вероятностей каждого из этих событий(гипотез) на соответствующие условные вероятности события F:
, образующих полную группу, то вероятность события F равна сумме произведений вероятностей каждого из этих событий(гипотез) на соответствующие условные вероятности события F:

Следствием теоремы умножения и формулы полной вероятности является формула Байеса:
Она применяется, когда событие F, которое может появиться только с одной из гипотез  , образующих полную группу событий, произошло или необходимо произвести количественную переоценку априорных вероятностей этих гипотез
, образующих полную группу событий, произошло или необходимо произвести количественную переоценку априорных вероятностей этих гипотез  , известных до испытания, то есть надо найти апостериорные(полученные после проведения испытания) условные вероятности гипотез
, известных до испытания, то есть надо найти апостериорные(полученные после проведения испытания) условные вероятности гипотез 

Или с учётом теоремы умножения:
 , получим:
, получим:

Аксиоматика Колмогорова:
Аксиома 1: Каждому событию вводится в соответствие некое неотрицательное число, которое будем называть вероятностью события P(A)
Аксиома 2:  - вероятность достоверного события равна 1.
- вероятность достоверного события равна 1.
 (здесь не тау должно быть, а омега заглавная буква, просто я не нашла такого символа) – множество исходов.
(здесь не тау должно быть, а омега заглавная буква, просто я не нашла такого символа) – множество исходов.
Исход – в результате эксперимента возможны несколько вариантов, эти варианты будут называться элементарными событиями или исходами.
Аксиома 3: Вероятность появления хотя бы одного из попарно независимых событий равна сумме вероятностей этих событий.

Свойства вероятностей:
1) Неотрицательность:

2) Нормированность (сумма вероятностей элементарных исходов равна 1)
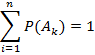
3) Вероятность события  равна сумме вероятностей элементарных исходов, в результате которых событие A может наступить:
равна сумме вероятностей элементарных исходов, в результате которых событие A может наступить:

Иногда для вычисления вероятности используют правила комбинаторики:
1) Перестановка: это упорядоченная выборка  элементов из
элементов из  :
:

2) Сочетание: Это неупорядоченная выборка  элементов из
элементов из  .
.
 , где
, где 
 - число сочетаний из n по m.
- число сочетаний из n по m.
3) Размещение: упорядоченная перестановка m элементов из n.

|
|
|


