 |
Распределение Фишера или F-распределение
|
|
|
|
Это распределение непрерывной случайной величины связанно с нормальным распределением. Если случайные величины 
, 
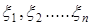(n, m – натуральные числа), независимы и каждое из них имеет нормализованное распределение, то случайная величина
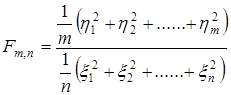(3.8)
имеет распределение Фишера с параметрами n и m, называемыми степенями свободы данного распределения.
F-распределение Фишера (для x > 0) имеет следующую функцию плотности (для степеней свободы m и n):
.
С увеличением числа степеней свободы распределение Фишера очень медленно стремится к нормальному.
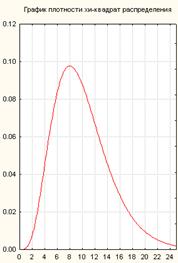
Графики плотности «хи-квадрат» распределения, t -распределения и распределения Фишера представлены на рис. 2.
а) б) в)
Рис 2. Графики плотности распределений:
а) хи-квадрат при числе степеней свободы m=10.
б) t-распределения при числе степеней свободы m=10.
в) Фишера для обеих степеней свободы равных 10.
Тема №8. Проверка гипотез
Пусть имеется выборка 
из генеральной совокупности с неизвестной теоретической функцией распределения.
Определение: Статистической гипотезой называется любое предположение о виде теоретической функции распределения. Имеются две непересекающиеся гипотезы: Н0 и H1. Н0 – нулевая (основная) гипотеза, H1 – альтернативная (конкурирующая) гипотеза. Принято считать, что Н0 –гипотеза о сходстве, H1 –гипотеза о различии.
Определение: Статистическим критерием (тестом) называется правило, позволяющее на основании наблюдений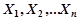 
принять нулевую гипотезу Н0 или отвергнуть ее в пользу альтернативной H1.
Определение: Критическую область составляют те значения выборочных статистических показателей, которые ведут к отказу от нулевой гипотезы.
Возможные решения статистического критерия:
|
|
|
| Результат проверки гипотезы | Возможные состояния проверяемой гипотезы | |
| Верна гипотеза Н0 | Верна гипотеза H1 | |
| Н0 отклоняется | Ошибка I рода | Правильное решение |
| Н0 не отклоняется | Правильное решение | Ошибка II рода |
Определение: Уровень значимости – вероятность ошибочного отклонения нулевой гипотезы Н0 (вероятность ошибки I рода). При статистическом анализе исследователь должен выбрать необходимый уровень значимости. При этом считают низшим уровнем значимости значение p =0.05, достаточным уровнем - p =0.01, высшем уровнем p =0.001.
Этапы принятия статистического решения:
1) Формулировка нулевой и альтернативной гипотез.
2) Определение объема выборки.
3) Выбор соответствующего уровня значимости или вероятности отклонения гипотезы Н0 (
).
4) Выбор статистического метода, который зависит от типа решаемой задачи.
5) Вычисление значения выборочной статистики 
на основании наблюдений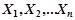 
.
6) Если гипотеза Н0 верна, то распределение случайной величины 
известно (затабулировано).Нахождение по таблице для выбранного статистического метода критической области 
для определенного уровня значимости.
7) Сравнение эмпирического и критического значений. Если 
, то принимается Н0; если 
, то Н0 отвергается в пользу альтернативной.
8) Формулировка принятия решения (выбор гипотезы Н0 или H1).
При попадании выборочной статистики в зону незначимости принимается гипотеза Н0 об отсутствии различий. В случае попадания в зону значимости принимается гипотеза H1 о наличии различий, а гипотеза Н0 отклоняется. При попадании выборочной статистики в зону неопределенности в зависимости от важности решаемой задачи можно принять H1 на уровне 5% или принять Н0 на 1% уровне. В этом случае можно допустить ошибки I или II рода. В этих обстоятельствах лучше увеличить объем выборки.
Проверка гипотезы может быть односторонней или двусторонней.
|
|
|
Определение: Односторонний критерий используется в тех случаях, когда необходимо знать, является ли параметр генеральной совокупности > (правосторонний критерий) или < (левосторонний критерий) предполагаемого значения.
Определение: Двусторонний критерий используется в тех случаях, когда интересует, отличаются ли реальные значения параметра от предполагаемого значения.
Проверка гипотезы о соответствии исправленной выборочной дисперсии величине генеральной дисперсии нормальной совокупности.
Стандартизированный статистический критерий (тест) для проверки такой гипотезы рассчитывается как: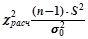 
, (1)
где σ02 – проверяемое значение генеральной дисперсии, а S2 – исправленная выборочная дисперсия,
Левосторонняя проверка: нулевая и альтернативная гипотезы имеют вид:
Н0: S2=σ2 – равенство неизвестной генеральной дисперсии S2;
Н0: S2<σ2.
Правило принятия решения: принять Н0, если 
, отвергнуть Н0, если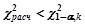 
. Здесь α – уровень значимости принятия гипотезы, k=n-1 – число степеней свободы 
- определяется по таблице χ2 –распределения (приложение 3).
Правосторонняя проверка: нулевая и альтернативная гипотезы имеют вид:
Н0: S2=σ2 – равенство неизвестной генеральной дисперсии S2;
Н0: S2>σ2.
Правило принятия решения: принять Н0, если 
, отвергнуть Н0, если 
.
Двусторонняя проверка: нулевая и альтернативная гипотезы имеют вид:
Н0: S2=σ2 – равенство неизвестной генеральной дисперсии S2;
Н0: S2≠σ2.
Правило принятия решения: принять Н0, если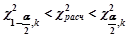 
, отвергнуть Н0 в противном случае.
Проверка гипотезы о соответствии выборочной средней величине генеральной средней нормальной совокупности.
Формируем гипотезы о равенстве генеральной и выборочной средней.
Н0: μ=μ0;
Н1: μ≠μ0.
Правило принятия решения: принять Н0, если 
, в противном случае принять Н1. Zкрит определяется из таблиц функции Лапласа из равенства Ф(zкрит)=(1-α)/2.
|
|
|
