 |
Классификация кинематических пар
|
|
|
|
ТЕОРИЯ МЕХАНИЗМОВ
И МАШИН
Учебное пособие
Самара
Самарский государственный технический университет

| МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» |
Кафедра "Механика"
 Е.К. КИЧАЕВ, А.М. ЛАШМАНОВ,
Е.К. КИЧАЕВ, А.М. ЛАШМАНОВ,
П.Е. КИЧАЕВ, Л.А. ДОВНАР
ТЕОРИЯ МЕХАНИЗМОВ
И МАШИН
Учебное пособие
Самара
Самарский государственный технический университет
Печатается по решению редакционно-издательского совета СамГТУ
УДК 621. 01
К 46
Кичаев Е.К.
К 46 Теория механизмов и машин: учеб. пособ. 2-е издание, перераб. / Е.К. Кичаев, А.М. Лашманов, П.Е. Кичаев, Л.А. Довнар. – Самара: Самарс. Гос. техн. ун-т, 2012. – 232 с.: ил.
ISBN 978-5-7964-1499-6
Описаны методы структурного, кинематического и динамического анализа рычажных механизмов. Рассмотрены основные принципы синтеза зубчатых механизмов. Материал изложен с учетом требований и стандартов; представлены как графоаналитические, так и аналитические методы определения параметров механизмов и машин.
Предназначено для студентов технических вузов при решении самостоятельных практических работ и выполнении курсового проекта по теории механизмов и машин. Оно также может быть рекомендовано для студентов дневной и заочной форм обучения по направлениям 130500, 150000, 190000, 200500, 280000 при изучении курса «Теория механизмов и машин».
УДК 621. 01
К 46
Рецензент: канд. техн. наук, доц. В.А. Дмитриев
ISBN 978-5-7964-1499-6 © Е.К. Кичаев, А.М. Лашманов,
П.Е. Кичаев, Л.А. Довнар, 2012
|
|
|
© Самарский государственный
технический университет, 2012
СОДЕРЖАНИЕ
| Предисловие……………………………………………………………….. | |
| Введение……………………………………………………………………. | |
| 1. Календарный план освоения курса…………………………………….. | |
| 2. Теоретический курс……………………………………………………... | |
| 2.1. Лекция №1. Структурный анализ механизмов………………… | |
| 2.2. Лекция №2. Кинематический анализ механизмов……………... | |
| 2.3. Лекция №3. Силовой анализ механизмов………………………. | |
| 2.4. Лекция №4. Динамический анализ механизма………………… | |
| 2.5. Лекция №5. Виброзащита машин. ……………………………… | |
| 2.6. Лекция №6. Уравновешивание машин…………………………. | |
| 2.7. Лекция №7. Общие методы синтеза механизмов…………........ | |
| 2.8. Лекция №8. Проектирование прямозубых цилиндрических зубчатых передач…………………………………... | |
| 2.9. Лекция №9. Проектирование беззазорного зацепления………. | |
| 2.10. Лекция №10. Кинематика зубчатого зацепления…………….. | |
| 2.11. Лекция №11. Разновидности зубчатых зацеплений………….. | |
| 2.12. Лекция №12. Проектирование кулачковых механизмов…….. | |
| 2.13. Лекция №13. Трение в кинематических парах……………….. | |
| 2.14. Лекция №14. Расчет коэффициента полезного действия……. | |
| 2.15. Лекция №15. Изнашивание твердых тел……………………… | |
| 2.16. Лекция №16. Роботы-манипуляторы………………………….. | |
| 2.17. Лекция №17. Кинематика роботов-манипуляторов …………. | |
| 2.18. Лекция №18. Основы теории машин-автоматов……………... | |
| 3. Курсовой проект……………………………………………………........ | |
| 3.1. Альбом заданий…………………………………………………... | |
| 3.2. Методические указания…………………………………………. | |
| 3.3. Пример оформления расчетно-пояснительной записки и графической части………………………... | |
| 3.4. Перечень вопросов, выносимых на защиту проекта…………... | |
| 4. Оценка знания курса…………………………………………………..... | |
| Заключение……………………………………………………............. | |
| Приложения………………………………………………………………... | |
| Библиографический список……………………………………………….. |
ПРЕДИСЛОВИЕ
|
|
|
Теория механизмов и машин (ТММ) является первой общетехнической дисциплиной. Согласно учебным планам 5 поколения при подготовке бакалавров сокращаются учебные часы на общетехнические дисциплины, что создает затруднение для их успешного освоения. Подобная тенденция коснулась и курса ТММ. Так, например, для машиностроительных направлений односеместровый лекционный курс ТММ составляет 17 аудиторных часов с параллельным выполнением курсового проекта. В худшем положении находятся студенты факультетов дистанционной и заочной форм обучения. Обилие литературы по ТММ, как в теоретическом, так и в практическом аспектах, создает студентам затруднение в ее оптимальном выборе при выполнении самостоятельных контрольных работ, курсовых проектов и при подготовке к экзаменам. Единственным способом облегчения и улучшения качества в освоении предмета являются интерактивные методы обучения, которые требуют создания новых методических продуктов.
Данное пособие является одним из шагов в этом направлении, позволяя студентам в интерактивной форме на примере кривошипно-ползунных механизмов рассмотреть алгоритмы определения их параметров традиционными графоаналитическими и современными аналитическими методами.
Предлагаемое пособие не претендует на полноту изложения курса ТММ и не подменяет классические учебники, а является как бы «Путеводителем» при самостоятельном изучении предмета.
ВВЕДЕНИЕ
Теория механизмов и машин (ТММ) – наука об общих методах исследования свойств механизмов и машин (анализ) и проектирования их схем (синтез). Излагаемые в ТММ методы являются общими и не зависят от целевого назначения механизмов и машин.
Механизм – это система тел, предназначенная для преобразования движения одного или нескольких твердых тел в требуемое движение других тел относительно одного из них, принятого неподвижным.
Машина – устройство, выполняющее механические движения для преобразования энергии, материалов и информации.
|
|
|
Машины разделяются на:
а) двигатель – преобразующий один вид энергии в другой, например, двигатель внутреннего сгорания (ДВС);
б) рабочую машину – потребляющую энергию извне и совершающую полезную работу. Например, станки, прессы, насосы, конвейеры, качалки и т.д. В качестве исполнительного механизма рабочей машины часто используют рычажные механизмы.
Машинным агрегатом называют объединение двигателя и рабочей машины.
1. КАЛЕНДАРНЫЙ ПЛАН ОСВОЕНИЯ КУРСА
| № п/п недели | |
| 2.1. Лекция №1. Введение. Структурный анализ механизмов. Самоконтроль Рубежный контроль Выдача курсовой работы согласно п. 3.1 2.2. Лекция №2. Кинематический анализ механизмов Самоконтроль Рубежный контроль Готовность 1 листа курсового проекта 2.3. Лекция №3. Силовой анализ механизмов Самоконтроль Рубежный контроль 2.4. Лекция №4. Динамический анализ механизмов Самоконтроль Рубежный контроль Готовность 2 листа курсового проекта 2.5. Лекция №5. Виброзащита машин Самоконтроль Рубежный контроль 2.6. Лекция №6.Уравновешивание машин Самоконтроль Рубежный контроль 2.7. Лекция №7. Общие методы синтеза механизмов Самоконтроль Рубежный контроль Готовность 3 листа курсового проекта 2.8. Лекция №8. Проектирование прямозубых цилиндрических зубчатых передач Самоконтроль Рубежный контроль 2.9. Лекция №9. Проектирование беззазорного зацепления Самоконтроль Рубежный контроль Готовность 4 листа курсового проекта 2.10. Лекция №10. Кинематика зубчатого зацепления Самоконтроль Рубежный контроль 2.11. Лекция №11. Разновидности зубчатых зацеплений Самоконтроль Рубежный контроль 2.12. Лекция №12. Проектирование кулачковых механизмов Самоконтроль Рубежный контроль 2.13. Лекция №13. Трение в кинематических парах Готовность расчетно-пояснительной записки Самоконтроль Рубежный контроль 2.14. Лекция №14. Расчет коэффициента полезного действия Самоконтроль Рубежный контроль 2.15. Лекция №15. Изнашивание твердых тел Готовность курсового проекта к защите Самоконтроль Рубежный контроль 2.16. Лекция №16. Роботы-манипуляторы Самоконтроль Рубежный контроль 2.17. Лекция №17. Кинематика роботов-манипуляторов Защита курсового проекта Самоконтроль 2.18. Лекция №18. Основы теории машин-автоматов Самоконтроль Рубежный контроль Итоговый контроль | 17-18 |
|
|
|
2. ТЕОРЕТИЧЕСКИЙ КУРС
2.1. Лекция №1. Структурный анализ механизмов
Рассмотрим в качестве примера кривошипно-ползунный механизм (рис. 2.1), который лежит в основе двигателей внутреннего сгорания поршневых компрессоров и насосов, ковочных машин и прессов и т.д. Несмотря на специфические требования, они все имеют одинаковые зависимости, описывающие их структуру, геометрию, кинематику и динамику, что и является предметом изучения курса ТММ
 |

Р и с. 2.1. Пример плоского механизма с низшими парами
Схема машины:

1 – двигатель
2 – передаточный механизм
3 – исполнительный механизм
4 – регулятор
В качестве передаточного механизма используют фрикционные, цепные и зубчатые передачи.
Основными элементами механизма являются звенья и кинематические пары. Звеном называется одно или несколько жестко соединенных твердых тел, входящих в состав механизма. Основные типы звеньев механизмов представлены в прил. 1. Звенья разделяются на входные и выходные. Входное звено – звено, которому сообщается движение, преобразуемое механизмом в требуемые движения других звеньев. Выходное звено – звено, совершающее движение, для выполнения которого предназначен механизм. Звенья могут быть упругими (пружины, мембраны), гибкими (ремни, цепи, канаты), жидкими и газообразными (масло, вода, воздух). Кинематической парой называется подвижное соединение двух звеньев. Звенья пары могут соприкасаться по поверхностям, линиям и точкам. В зависимости то этого пары называются высшими (касание по линии или точке) и низшими (касание по поверхности). Существование пар обеспечивается условиями замыкания, сохраняющими постоянство контактов звеньев. Замыкание бывает геометрическим (обычно низшие пары) и силовым. Различают пары плоские, когда относительное движение звеньев происходит в параллельных плоскостях, и пространственные.
Основные виды механизмов – это рычажные, зубчатые и кулачковые. Рычажный механизм – это механизм, звенья которого образуют только вращательные, поступательные, цилиндрические и сферические пары. Зубчатый механизм (зубчатая передача) – передаточный механизм, в котором подвижными звеньями являются зубчатые колеса, образующие со стойкой или водилом вращательные или поступательные пары. Кулачковый механизм – механизм, в состав которого входит кулачок. Кулачок имеет рабочую поверхность переменной кривизны и образует с взаимодействующим с ним звеном высшую пару.
|
|
|
Кинематической цепью называют связанную систему звеньев, образующую кинематические пары. Открытая цепь – та, в которой имеются звенья, входящие в одну кинематическую пару (рис. 2.2).
Замкнутая цепь – это цепь, у которой все звенья входят не менее чем в две пары. Механизм представляет собой частный вид кинематической цепи, у которой одно звено обращено в стойку, а движение выходных звеньев вполне определяется заданным движением входных (исключение для механизмов манипуляторов). Механизмы бывают пространственные и плоские; рычажные, когда звенья образуют лишь низшие пары; шарнирные, когда имеются лишь вращательные пары. Кинематические цепи разделяют на классы в зависимости от числа условий связи, налагаемых на относительное движение двух звеньев. Тело в пространстве имеет шесть степеней свободы. Если обозначить число связей налагаемых кинематической парой через U, то
W = 6 – U, (2.1)
где W – относительное число степеней свободы двух звеньев.


Р и с. 2.2. Механизм манипулятора
Кинематические пары обозначаются как Р 1, Р 2, …, Р 5, т.е. пары 1, 2, …, 5 классов. Примеры различных кинематических пар представлены в табл. 1.2.
Степень свободы пространственных кинематических цепей определяется по формуле Малышева (1923):
W = 6 n – 5 p 5 – 4 p 4 – 3 p 3 – 2 p 2 - p 1 = 6 n -  i × Pi, (2.2)
i × Pi, (2.2)
где n – число подвижных звеньев.
Степень подвижности плоской кинематической цепи подсчитывается по формуле Чебышева (1869):
W = 3 n – 2 p 5 – p 4 = 3 n -  (i -3) Pi. (2.3)
(i -3) Pi. (2.3)
Примечание: на плоскости существуют только пары 4 и 5 классов, причем пары 5 класса являются низшими, т.е. касание звеньев происходит по поверхности. Это могут быть вращательные и поступательные пары. Каждая низшая пара рнп накладывает два условия связи, а высшая рвп одно.
Формула (2.3) верна лишь для статически определимых систем.
Согласно формуле Чебышева плоский кривошипно-ползунный механизм (рис. 2.1) имеет степень подвижности W = 1. За счет погрешностей при изготовлении и сборке возможны натяги в кинематических парах и деформации звеньев, т.е. возникают избыточные контурные связи q, число которых можно определить, если рассматривать механизм как пространственный. В рассмотренном механизме
q = W – 6 n + 5 p 5 = 1 - 6×3 + 5×4 = 3. 
Для исключения этих трех избыточных связей следует применять более подвижные цилиндрические и сферические кинематические пары. Например, если пару в т.А представить как цилиндрическую, а в т.В как сферическую, то q = 1 - 6×3 + 5×2 + 4×1 + 3×1 = 0, и механизм становится статически определимым.
Часто при структурном и кинематическом анализе плоский механизм рассматривают лишь с низшими парами, используя замену высших пар на низшие. Правило следующее: любая высшая кинематическая пара может быть заменена одним дополнительным звеном с двумя низшими парами, причем, длина этого звена равна суммарному радиусу кривизны сопряженных поверхностей высшей пары. Составляя схему нового механизма, конструктор должен в самой начальной стадии проектирования правильно выбрать ее структуру, убедиться в ее работоспособности. Структурный синтез проводится без определения размеров звеньев и базируется на учении о кинематических парах, степенях свободы кинематических цепей.
В 1911 году профессор Л.В. Ассур дал рациональную классификацию плоских механизмов, которая позволила все плоские механизмы разбить на классы, для которых возможны единые методы кинематических и динамических расчетов. Согласно методике Ассура и уточнению И.И. Артоболевского любой механизм может быть получен путем подсоединения к базовым (звено со стойкой) групп Ассура. Основное свойство группы – равенство степени подвижности нулю. Базовые механизмы отнесены к первому классу (турбины, электродвигатели, цилиндр с поршнем…). Согласно формуле (2.3) при Wгр = 0 соотношение звеньев и низших кинематических пар следующее:
| n | |||
| рнп | |||
| Кл. |
Класс механизма определяется по наиболее высокому классу групп Ассура, входящих в механизм.
Основной прием структурного анализа механизма состоит в том, что от механизма (начиная от выходного звена) отсоединяется простейшая группа Ассура (диада), т.е. два звена и три кинематические пары, после чего оставшаяся часть должна составлять замкнутую кинематическую цепь. В противном случае нужно отсоединять более сложные группы. Операцию повторяют до тех пор, пока не останутся базовые механизмы, а их количество равно степени подвижности механизма. Различные виды групп Ассура и примеры механизмов, получающихся при их присоединении к базовому механизму, представлены в табл. 2.2. Порядком группы является число кинематических пар, которыми группа подсоединяется к механизму.
Таблица 2.1
Классификация кинематических пар
| Наименование пары | Класс пары | Подвижность | Схема пары | Условные обозначения |
| Точечная | 
| 
| ||
| Линейная |

| 
| ||
| Плоская | 
| 
|
Окончание табл. 2.1
| Наименование пары | Класс пары | Подвижность | Схема пары | Условные обозначения |
| Сферическая | 
| 
| ||
| Цилиндрическая | 
| 
| ||
| Винтовая | 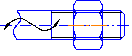
| 
| ||
| Поступательная | 
| 
| ||
| Вращательная | 
| 
|
Таблица 2.2
|
|
|


