Кинематика многозвенных зубчатых механизмов

Многоступенчатые передачи имеют две разновидности: колеса с неподвижными осями и передачи эпициклические. Колеса с неподвижными осями разделяются на простой ряд зубчатых колес и ступенчатые передачи.

Простой ряд зубчатых колес – такой ряд колес, когда на каждой из осей находится только по одному зубчатому колесу (рис. 2.41).

, k – число внешних передач. Промежуточные колеса служат для реверса.

	z2		z3

w1

w3

w2

z1

о2

о1

о3

 

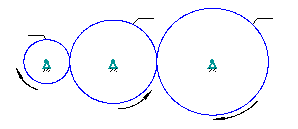
Р и с. 2.41. Простой ряд зубчатых колес

 

Ступенчатые передачи – такие передачи, когда имеется хотя бы один вал, на котором находится два или несколько зубчатых колес (рис. 2.42).

 

; ; ; (2.80) .

Р и с. 2.42. Ступенчатая передача

 

Эпициклические передачи – это такие передачи, в которых имеется хотя бы одна ось, на которой находятся колеса, вращающиеся одновременно вокруг нее и вместе с ней. Они делятся на дифференциальные (с двумя степенями свободы) и планетарные. Пример дифференциального механизма представлен на рис. 2.43, где Z ₁, Z ₃ – солнечные (центральные) колеса; Н – водило; Z ₂ – сателлит.

W =3 n -2 p_нп - р_вп =3´4-2´4-2=2

Из четырех угловых скоростей (w ₁, w ₂, w ₃, w_н) две должны быть независимыми.

Методика определения передаточного отношения следующая: примем водило неподвижным, получаем обращенный механизм.

w ₁½ w ₁- w_н = w׳ ₁

w ₃½ w₃- w_н = w׳ ₃ U ₁₃ ^н = w׳ ₁/ w׳ ₃=(w ₁- w_н)/(w ₃- w_н)=- Z ₃/ Z ₁.

w_н ½ w_н - w_н =0

При w ₃=0 полученная передача имеет одну степень подвижности и называется планетарной (рис. 2.44).

U ₁₃ ^н =(w ₁- w_н)/(- w_н)=1- U _{1 н} ³; U _{1 н} ³=1- U ₁₃ ^н (2.81)

Примечание: верхний индекс в передаточном отношении указывает на неподвижность звена.

 

 

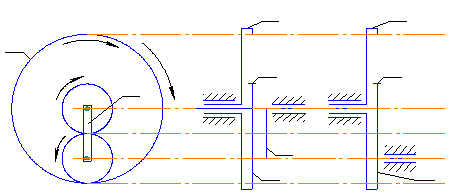
Р и с. 2.43. Дифференциальный механизм

 

Передаточное отношение планетарного механизма равно единице минус передаточное отношение обращенного механизма. Планетарные передачи являются малогабаритными и, как правило, их выгодно использовать при передаточных отношениях от 20 до 200.

Рассмотрим примеры.

Z1=Z3=100; Z2=99;Z4=101; (2.82) U1н4=1-U14н=1/10000; U14н=Z2´Z4/Z1´Z3=99´101/100´100=0,9999.

Р и с. 2.44. Планетарный

механизм

Z ₁, Z _2, Z ₃ – конические шестерни дифференциала (рис. 2.45) заднего моста автомобилей «классика» (работают на повороте); Z _5, Z ₄. Н – передача от мотора на корпус дифференциала; А, В – колеса заднего моста.

 

 

Р и с. 2.45. Конический дифференциал

 

n_н =(n ₁+ n ₂)/2 ; n ₁- n_н =-(n ₃- n_н). (2.83)

 

Волновые передачи

Н – генератор волн, который вставляют внутрь гибкого колеса 2 (рис. 2.46). Он представляет собой водило с двумя роликами 1, которые растягивают колесо 2 и оно своими зубьями входит в зацепление с жестко закрепленным колесом 3.

U_н2³=1/U_2н³=1/(1-U₂₃^н)=-Z₂/(Z₃-Z₂)=-Z₂/2. (2.84)

Например, при Z₂=200; Z₃=202; U_н2³=-100.

 

Н z1 z1 z2 z3   Р и с. 2.46. Волновая передача

Преимущества волновой передачи по сравнению с планетарной: - в зацеплении находится много пар зубьев и возможна передача большего крутящего момента; - зубья могут быть выполнены с меньшей точностью;

- передача может быть герметичной.

Недостаток – колесо 2 должно быть выполнено из высокопрочного материала, например, сталь 12ХН3А.

2.11. Лекция №11. Разновидности
зубчатых зацеплений

Разновидности плоских зубчатых зацеплений:

- реечное зацепление при r_в ®¥;

- внутреннее зацепление имеет малые габариты и больший коэффициент перекрытия;

- косозубое зацепление представлено на рис. 2.47,

где Р_n – нормальный шаг, Р_s – торцовый шаг.

. (2.85)

 

Р и с. 2.47. Косозубое колесо

 

При одном и том же нормальном модуле косозубые колеса имеют бóльшие диаметры и бóльший коэффициент перекрытия.

Пространственные зубчатые зацепления (2.48) возникают в тех случаях, когда оси зубчатых колес I-I и II-II или пересекаются, или перекрещиваются. При этом образующие поверхности представляют собой гиперболоиды вращения.

Практически используют периферийные части, заменяя их конусами. Если оси пересекаются, то зацепление называется коническим, а если перекрещиваются – гипоидными. Используя средние части гиперболоидов, заменяют их цилиндрами. Полученная передача называется винтовой.

Р и с. 2.48. Гиперболоиды вращения

 

d 2 r 2 d 1 r 1   П mн mв О   Р и с. 2.49. Коническая передача

Коническое зацепление представлено на рис. 2.49. Окружности радиусов ρ 1 и ρ 2 можно считать начальными окружностями цилиндрических колес, обладающих таким же шагом и модулем, как и цилиндрические колеса. В связи с этим за стандартный принимают модуль mн –

наружный, а m_ср, m_вн – средний и внутренний модули. При расчетах на прочность за расчетный берется средний модуль.

. (2.86)

При , ctg δ, а передача называется ортогональной.

; аналогично для 2-го колеса.

. (2.87)

Z ₁, Z ₂ – число зубьев конических колес. Z _{1 ф} , Z _{2 ф} – число зубьев воображаемых

r1

(фиктивных) колес, т.е. Z ₁ может быть меньше 17 (обычно ³ 14). Нарезание конических колес производится методам обкатки.

 

 

Р и с. 2.50. Разновидности зубьев конических колес:

1 – прямой; 2 – спиральный; 3 – тангенциальный; 4 – круговой

 

К недостаткам винтовой передачи относят неизбежную скорость скольжения зубьев и наличие точечного контакта. По геометрии винтовые колеса ничем не отличаются от косозубых колес. Пример винтовых зубчатых колес представлен на рис. 2.51, соответственно I-I и II-II оси колес.

; (2.88)

;

.

Частным случаем винтовой передачи является червячное зацепление, т.е. оси скрещиваются под прямым углом (рис. 2.52). Червяк делают стальным каленым, а венец колеса – бронзовым. Преимуществами червячной передачи являются: малые габариты и необратимость, когда вращение передается только от червяка к колесу (самоторможение).

Основной недостаток передачи – сильное трение в зацеплении. Отсюда – низкий кпд и высокая рабочая температура.

Z ₁= q; Z ₂≤ 120; q =1¸5 – число заходов червяка.

 

Р и с. 2.51. Винтовая передача

Р и с. 2.52. Червячные передачи

 

Контрольные вопросы

1. Какие передачи применяются для передачи движения между валами, оси которых параллельны?

2. Какие передачи применяются для передачи движения между валами, оси которых пересекаются?

3. Какие передачи применяются для передачи движения между валами, оси которых перекрещиваются?

4. Какие передачи работают на принципе зацепления?

5. Какие передачи работают на принципе трения?

6. Какой параметр может быть положительным, отрицательным или равным нулю?

7. У какой передачи передаточное отношение будет отрицательным?

8. У какой передачи передаточное отношение будет положительным?

9. У какой передачи передаточное отношение будет равно нулю?

10. У какой передачи передаточное отношение будет равно бесконечности?

11. Для какой передачи коэффициент перекрытия равен сумме торцового и осевого коэффициентов перекрытия?

12. Чему равно (по модулю) передаточное отношение зубчатой пары, если угловая скорость ведущего колеса равна 1000 об/мин., а угловая скорость ведомого – 500 об/мин.?

13. Чему равен угол зацепления равносмещенной косозубой передачи торцовом сечении?

Полностью материал по данной теме изложен в учебниках [1, с. 361-412], [2, с. 234-295], [3, с. 133-169], [4, с. 44-52], [5, с. 253-271], [6, с. 72-81].

2.12. Лекция №12. Проектирование
кулачковых механизмов

Кулачок – профильное звено, геометрия которого определяет закон движения исполнительного звена, именуемого толкателем. Кулачок с толкателем составляют высшую кинематическую пару. В связи с этим исключается возможность передачи больших усилий, поэтому, несмотря на простоту, кулачковые механизмы применяются как вспомогательные (механизмы зажимов, переключателей, распредвалов, насосов и т.д.). Работа кулачкового механизма должна быть согласована с работой основного механизма машины, то есть в качестве исходных данных для проектирования кулачковых механизмов служит циклограмма работы соответствующего основного механизма.

На рис. 2.53 представлены кулачковые механизмы с поступательно движущимся остроконечным толкателем, с коромысловым остроконечным толкателем и с тарельчатым толкателем.

 

а) б) в)

 

 

Р и с. 2.53. Разновидности толкателей:

a) остроконечный; б) коромысловый; в) тарельчатый (плоский)

Остроконечные толкатели более точно передают заданный закон движения, но имеют повышенный износ. Поэтому в большинстве случаев их заменяют роликовыми толкателями. Тарельчатый толкатель обеспечивает нулевое значение угла давления, т.е. совпадение направления силы и перемещения толкателя, но профиль кулачка в этом случае должен быть выпуклым. Исходные данные для проектирования кулачкового механизма:

1. Максимальное перемещение толкателя.

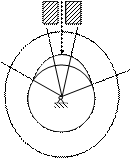
2. Фазовые углы профиля кулачка (рис. 2.54): j_у – угол удаления; j_дс – угол дальнего стояния; j_в – угол возвращения; j_бс – угол ближнего стояния.

В частных случаях углы ближнего или дальнего стояния могут быть равны нулю. Углы удаления, дальнего стояния и возвращения в сумме составляют угол рабочего профиля кулачка:

j_у + j_дс + j_в = j_р. (2.89)

3. Закон движения толкателя.

Если для технологической операции закон движения толкателя непринципиален, то на фазе удаления и возвращения следует выбирать законы без жестких и мягких ударов. Жесткий удар возникает в случае, когда скорость толкателя мгновенно достигает конечной величины. При этом теоретически ускорение будет бесконечным. Следовательно, сила инерции толкателя также будет бесконечной. Мягкий удар возникает в случае, когда ускорение толкателя достигает конечной величины. При этом возникает сила инерции, но ее значение не настолько велико, чтобы привести к поломке механизма. В соответствии с вышесказанным, закон движения толкателя обязательно проверяется на плавность ускорения. Лучшими законами считаются тригонометрические функции или кривые степени более трех. Поставленная задача имеет множество решений. Как правило, оптимизацию производят по минимизации габаритов механизма, при этом мерой является минимальный радиус кулачка r_о.

Для остроконечного или роликового толкателя определение минимального радиуса кулачка основывается на условии незаклинивания механизма, которое связано с понятием угла давления.

Р и с. 2.54. Основные параметры кулачка

 

Угол давления – это угол между нормалью к профилю кулачка в точке касания и абсолютной скоростью толкателя, если пренебречь силами трения. При достижении углом давления некоторой величины (для поступательно движущегося толкателя ~ 30°) в опоре штанги толкателя происходит заклинивание. Связь между углом давления и минимальным радиусом кулачка выражается формулой

tgJ =(dS / dj ± e)/( + S (j)), (2.90)

где ds / dj – текущий аналог скорости толкателя;

е – эксцентриситет (несовпадение штанги толкателя с осью вращения кулачка);

S (j) – текущее перемещение толкателя.

Из формулы (2.90) видно, что между углом давления и минимальным радиусом кулачка существует обратная зависимость.

Для плоского или тарельчатого толкателя необходимо, чтобы радиус кривизны всегда был больше 0, т.е. профиль кулачка должен быть выпуклым. Кулачок имеет выпуклый профиль, если радиус его в любом положении удовлетворяет условию

r_o >[ S + d ² S / dj² ]. (2.91)

Профилирование кулачка производится методом обращенного движения, т.е. всему механизму придается вращение -w_к. Тем самым мы заставляем толкатель вращаться вокруг кулачка, одновременно перемещая его согласно заданному закону движения. Построенный таким образом профиль кулачка называется теоретическим. В случае остроконечного толкателя он же является рабочим профилем. Если толкатель роликовый, то теоретический профиль представляет собой последовательность центров ролика. Касательная к роликам (эквидистанта) будет рабочим профилем кулачка. В случае тарельчатого толкателя касательная к тарелкам, построенным по теоретическому профилю, будет рабочим профилем кулачка.

 

Контрольные вопросы

1. Почему применяются кулачковые механизмы?

2. Зачем ставится ролик на остроконечный толкатель?

3. Для чего применяется тарельчатый толкатель?

4. По какому критерию определяется минимальный радиус кулачка с остроконечным толкателем?

5. По какому критерию определяется минимальный радиус кулачка с тарельчатым толкателем?

6. Что такое теоретический профиль кулачка с роликовым толкателем?

7. Что такое рабочий профиль кулачка с роликовым толкателем?

8. В каких точках происходит максимальный износ профиля кулачка с роликовым толкателем?

 

Полностью материал по данной теме изложен в учебниках [1, с. 422-454], [2, с. 296-320], [3, с. 173-185], [4, с. 52-55], [5, с. 272-315].

2.13. Лекция №13. Трение в кинематических парах

Природа и виды трения

Сопротивление, возникающее на поверхности двух соприкасающихся тел при их относительном движении, называется силой внешнего трения. При движении одного тела относительно другого происходит сцепление, возникают упругие, вязкие деформации, развиваются силы молекулярного взаимодействия. Энергия затрачиваемая на трение, превращается в теплоту, происходит сглаживание шероховатостей, называемое износом.

В зависимости от взаимодействия различают:

- трение скольжения – как в низших, так и высших парах (1 рода);

- трение качения – при перекатывании поверхностей, встречается только в высших парах (2 рода);

- трение верчения – относительное движение вокруг общей нормали и все точки описывают концентрические окружности.

Взависимости от состояния поверхностей различают:

- сухое трение – без всяких примесей;

- граничное трение – слой смазки менее ≈ 0,1 мкм;

- жидкостное трение – слой смазки полностью разделяет поверхности соприкасающихся тел;

- трение с газовой смазкой.

Основные зависимости при трении скольжения

Сухое трение.

F_тр = F_мол + F_мех,

где F_тр – сила трения при скольжении;

F_мол – сила трения, определяемая силами молекулярного взаимодействия контактирующих элементов;

F_мех – сила трения механических связей.

 

F_тр = μ_т·S_ф + ƒ·N,

где μ_т – интенсивность молекулярной силы трения;

S_ф – фактическая площадь контакта;

N – нормальное давление;

ƒ – коэффициент трения, безразмерная величина, зависит от материала и состояния поверхности и т. д.

На практике применяют

F = ƒ·N. (2.92)

Различают коэффициент трения покоя ƒ₀ > ƒ, когда сила трения покоя характеризуется отсутствием относительного движения двух соприкасающихся тел при действии на них касательных сил.

Основные закономерности сухого трения:

- силы трения направлены противоположно относительным скоростям;

- с увеличением скорости, сила трения уменьшается;

- с возрастанием удельного давления ƒ увеличивается;

- с увеличением времени контакта, сила трения возрастает.

Жидкостное трение. Жидкостное трение определяется гидродинамическими явлениями, возникающими в движущейся масляной пленке. Основным требованием, обеспечивающим жидкостное трение, является создание клиновидного зазора между трущимися поверхностями при большой скорости скольжения (рис. 2.55).

 

а) б) в)

 

Р и с. 2.55. Картина образования
масляного клина при жидкостном трении:

а – в поступательной паре; б, в – во вращательной паре

 

Современная гидродинамическая теория смазки подшипников Н.П. Петрова (1883) в упрощенном виде дает формулу

F = μ·V·S /ε, (2.93)

где μ – коэффициент абсолютной вязкости смазки;

V – скорость относительного скольжения;

S – поверхность соприкосновения твердых тел (шина с вкладышем);

ε – толщина слоя смазки.

И при ƒ^{* =} μ·V/ε·q

F = ƒ^*·N,

где ƒ^* – приведенный коэффициент трения, q = N/S – удельное давление, ƒ^* ≈ 0,005 ÷ 0,015.

Зависимость коэффициента трения от скорости относительного скольжения представлена на рис. 2.56.

 

Р и с. 2.56. Характер изменения приведенного

коэффициент трения от скорости относительного скольжения:

ab – граничное трение; b – точка всплывания; bc – жидкостное трение

 

Определение реакций в низших парах с учетом сил трения

Действительная реакция в поступательной паре (рис. 2.57) равна геометрической сумме сил и

 

= +

 

Она отклоняется от нормальной составляющей на угол трения ρ. Так как tg ρ, то f = tg ρ и, соответственно, ρ = arctg f.

Скалярная её величина

R₁₂ = = N₁₂ .

Сила трения отклоняет действительную реакцию от нормали на угол трения ρ в сторону противоположную скорости V₂₁.

Действительная реакция во вращательной паре с зазором также отклоняется на угол ρ, при этом создается момент трения (рис.2.58).

М_Т = T₁₂·r = R₁₂·h,

где h = r· sin ρ

 

Р и с. 2.57. Действие сил в поступательной паре

 

Учитывая что ρ <10˚, то sin ρ ≈ tg ρ≈ ƒ, тогда h ≈ r· ƒ, a М_Т = R₁₂· r·ƒ.

 

Р и с. 2.58. Действие сил во вращательной паре

 

Действительная точка касания цапфы с вкладышем при зазоре смещается на плечо h, зависящее от радиуса цапфы и коэффициента трения и направлена касательно кругу трения, радиусом h в противоположную сторону относительно угловой скорости ω.

 

 

Трение в высших парах

Сопротивление при качении определяется тем, что поверхностный слой упруго и пластически деформируется (рис. 2.59). Полоску контакта делят на участок сцепления и упругого скольжения.

M_T = КN,

где M_T – момент сопротивления;

N – нормальное давление;

К – коэффициент трения;

b – зона контакта.

Коэффициент K зависит от материалов, термообработки и т.д. Чем больше твердость материалов пары, тем меньше коэффициент сопротивления качению.

 

 

Р и с. 2.59. Трение качения

 

Условие чистого качения:

Сила тяги равна P = КN/r, так как ΣМ_А = 0 (Pr = КN).

F₀ сила трения покоя при F₀= ƒ₀ N.

При чистом качении необходимо, чтобы сила тяги была меньше силы трения покоя P ≤ ƒ₀·N. Соответственно ƒ₀ > К/r, т.е. осуществить чистое качение можно только при достаточном трении скольжения.

 

 

Примеры расчета трения в кинематических парах:

1. Перемещение груза на катках (рис. 2.60).

 

Р и с. 2.60. Трение груза на катках:

Q – вес плиты; G – вес одного катка

 

При симметричном нагружении в верхних точках катков общий момент сопротивления

М_с1 = Q·К₁.

В нижних

М_с2 = (Q + n·G)·К₂,

где n – число катков;

К₁, К₂ – коэффициент сопротивления при качении.

Движущая сила Р находится из уравнения моментов, составленного относительно полюса мгновенного вращения, т.е. точки касания катков с опорой

P·2r = Q·К₁ + (Q + n·G)·К₂.

Пренебрегая весом катков G ≈ 0 имеем:

P = Q[(К₁ + К₂)/(2r)].

Если принять, что Р = F = ƒ^*·Q, то приведенный коэффициент трения

ƒ^* = (К₁ +К₂)/(2r).

Перемещение груза на катках производят на небольшие расстояния, а при перемещении груза на большие расстояния применяют тележки с колесами.

2. Передвижение груза на направляющих роликах, вращающихся в подшипниках (рис. 2.61).

 

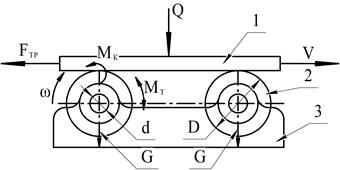
Р и с. 2.61. Трение груза на тележке

 

Общий момент сопротивления равен

М = М_К + М_Т. (2.94)

Момент сопротивления равен качению в паре 1-2

M_К= Q·К. (2.95)

В паре 2-3 трения скольжения

М_Т = (Q + n·G) ƒ^*· , (2.96)

где d – диаметр цапфы;

n –число роликов.

Полагая, что G ≈0 из (2.95) имеем М = Q (К+f^*·d/2).

Положим, что М = Q· , то приведенный коэффициент трения

равен = ƒ ^*+К / . Момент сил, приводящих во вращение катки равен

M_Т12 Т = Q·ƒ₁₂·D/2,

где D – диаметр роликов.

Осуществление чистого качения возможно при M_Т12>M, следовательно, ƒ₁₂·Q·D/2 > ƒ₀·Q· d/2

ƒ₁₂> ·d/D.

 

Необходимая движущая сила P = 2M/D = Q·ƒ ^*₀·d/D, т.е. для ее снижения нужно увеличить D и уменьшить d, уменьшить за счет смазки и уменьшить К при увеличении твердости.

3. Трение гибкой нити (рис. 2.62).

Трение гибкой нити встречается в ленточных тормозных устройствах и фрикционных передачах.

Теорию расчета гибкой нити по твердому телу (барабану) разработал в 1765 году Леонард Эйлер.

Σx = 0 = -ƒdN - S· cos (dα/2) + (S + dS)· cos (dα/2) = 0

Σy = 0 = -S· sin (dα/2) + dN - (S + dS)· sin (dα/2),

где ƒ – коэффициент трения;

dα – бесконечно малый угол обхвата.

 

Р и с. 2.62. Трение гибкой нити

 

Принимая sin (dα/2) = dα/2; cos (dα/2) ≈ 1 и пренебрегаем dS(dα/2) = 0 получим

-ƒdN – S + S + dS = 0 => ƒdN = dS;

dN - S·dα/2 - S·dα/2 = 0 => dN = S·dα;

ƒdα = dS/S => ƒ·S·dα = dS;

= => ƒα = ln(S₁/S₂) => e^ƒα = S₁/S₂;

S₁ = S₂ e^ƒα.

Сила трения о барабан T = S₁-S₂.

Вращающий момент ременной передачи

M = S₂·R·(e^ƒα – 1)=S₁R(1- ).

 

Контрольные вопросы

1. Что называется силой внешнего трения?

2. Какие бывают разновидности внешнего трения от взаимодействия соприкасающихся поверхностей?

3. Какие существуют разновидности внешнего трения от состояния поверхностей?

4. От чего зависит сухое трение скольжения?

5. От чего зависит жидкостное трение скольжения?

6. Что является общим для сухого и жидкостного трения скольжения?

7. Как зависит коэффициент трения скольжения от скорости относительного движения?

8. Как определяют реакцию во вращательной и поступательной парах при трении скольжении?

9. Почему при качении возникает трение?

10. Как рассчитывается коэффициент внешнего трения в кинематических парах?

 

Полностью материал по данной теме изложен в учебниках [1, с. 206-284], [2, с. 343-349], [3, с. 81-92].

2.14. Лекция №14. Расчет коэффициента
полезного действия

Энергетическая характеристика машинного агрегата на стадии установившего движения имеет вид

А_дс = А_пс + А_вс, (2.97)

где А_дс – работа движущих сил за цикл движения машинного агрегата;

А_пс – работа сил полезного сопротивления за цикл движения машинного агрегата;

А_вс – работа сил вредного сопротивления за цикл движения машинного агрегата.

Механическим КПД машины η называется отношение работы сил полезных сопротивлений А_пс к работе движущих сил А_дс за период установившегося движения

 

η = А_пс/А_дc = (А_дc - А_вс)/А_дc = 1 - А_вс/А_дc = 1 – æ, (2.98)

 

где æ = А_вс/А_дс – коэффициент потерь.

Данный критерий удобно применять для отдельных механизмов и кинематических пар.

При расчете мгновенного КПД, отношение работ заменяют отношением мощностей.

Механизм может быть получен путем соединения кинематических цепей последовательно или параллельно.

Полный КПД при последовательном соединении (рис. 2.63) равен произведению частных КПД η = η₁·η₂·η₃… η_n

 

 

Р и с. 2.63. Полный КПД

при последовательном соединении

 

При параллельном соединении механизмов (рис. 2.64), полный КПД вычисляется по формуле (2.99)

η = η₁·k₁ + η₂·k₂ + η₃·k₃ + … η_n·k_n, (2.99)

где k₁, k₂… k_n – коэффициенты распределения энергии;

k₁ + k₂ +… k_n = 1.

А₁=А_д∙k₁, А₂= А_д∙k₂, …, А_n∙k_n= А_д∙k_n.

A₁+A₂+…A_n=A_nc

 

Р и с. 2.64. Полный КПД при параллельном соединении

 

Смешанное соединение рассматривают по цепям (рис. 2.65):

η = k₁(η₁·η_1/2) + k₂(η₂·η_2/2)

 

 

 

Р и с. 2.65. Полный КПД при смешанном соединении

 

КПД типовых механизмов . КПД винтовых механизмов может быть вычислено приближенно по формуле для КПД наклонной плоскости. При этом средняя линия прямоугольной резьбы заменяется наклонной плоскостью, а гайка – ползуном (рис. 2.66).

 

 

Р и с. 2.66. КПД наклонной плоскости

 

Реакция R винта, отклонена на угол φ от нормали и на (β+φ) от вертикали. Суммарный момент реактивных сил R относительно оси винта

М = r·R ·sin(β+φ), (2.100)

где r – средний радиус резьбы.

Из уравнений проекций связь реактивной силы R с заданной осевой силой Q имеет вид:

Q = cos(β+φ) = R· cos(β+φ). (2.101)

Окончательно движущий момент необходимый на подъем гайки:

 

М = Q·r· tg(β+φ), (2.102)

 

полагая, что трение отсутствует, то ƒ = 0 и, соответственно, φ = 0. Тогда из (2.102):

М = Q·r ·tg β.

Следовательно, КПД равен

η = tg β /tg(β+φ). (2.103)

 

КПД механизмов с низшими парами:

1. Приближенный метод – метод приведения сил: определяются реакции без трения, а затем учитываются силы трения.

2. Точный метод – метод кругов и углов трения, определение реакций с учетом сил трения.

Пример: кривошипно-ползунный механизм.

 

l

 

Р и с. 2.67. КПД кривошипно-ползунного механизма

 

Дано: R₀₁, R₁₂,R₂₃, R₀₃, d₀₁, d₁₂, d₂₃, ƒ^*₀₁, ƒ₀₃, ƒ^*₁₂, ƒ^*₂₃, r, l, ω₁, F_nc

 

η = 1- N_вс/N_дс

где N_дс = N_nc + N_T01 + N_T12 + N_T23 + N_T03; N_nc = F_nc·V_C

N_T01 = R₀₁·ƒ^*₀₁·d₀₁/2 ω₁ = R₀₁·ƒ^*₀₁·V_B·(d₀₁/2r);

(R₀₁·ƒ^*·V_В(d₀₁/2r))/N_дс = æ₀₁

N_T03 = R₀₃·ƒ₀₃·V_C (R₀₃·ƒ₀₃·V_C)/N_дс = æ₀₃

N_T23 = R₂₃·ƒ^*₂₃·(d₂₃/2)·ω₂ = R₂₃·ƒ^*₂₃·V_CB·(d₂₃/2l)

R₂₃·ƒ*₂₃·V_CB·(d₂₃/2l)/N_дс = æ₂₃

N_T12 = R₁₂·ƒ^*₁₂·(d₁₂/2)·ω₁₂ = R₁₂·ƒ^*₁₂·(d₁₂/2)·(V_CB/l + V_B/r)

+

ω₁₂ = ω₁ + ω₂ = V_B/r + V_CB/l R₁₂·ƒ^*₁₂·d/2·(V_CB/l + V_B/r)/N_дс = æ₁₂

 

η = 1 – æ₀₁ - æ₀₃ - æ₂₃ – æ₁₂ при ƒ = const, d_ij = const.

 

Контрольные вопросы

1. Что называется механическим КПД?

2. Зачем нужно знать мгновенный КПД?

3. Что такое коэффициент потерь?

 

Полностью материал по данной теме изложен в учебниках [1, с. 206-284], [2, с. 343-349], [3, с. 81-92].

2.15. Лекция №15. Изнашивание твердых тел

Основные понятия и определения

Изнашивание – это

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: