2.2. Закономерности распределения вероятностей отказов

Отказы в строительном производстве представляют собой случайные величины, которые могут быть дискретными и непрерывными в зависимости от физического смысла исследуемого явления, и характеризуются функциями распределения вероятностей.

Если  - случайная величина, то вероятность того, что она примет значение, меньшее некоторого числа х

,                                                                     (2. 5)

называется интегральной функцией распределения вероятностей или законом распределения вероятностей случайной величины отказов.

Для случайных дискретных величин F(x) есть неубывающая ступенчатая функция; для непрерывных случайных величин F(x) непрерывная функция для всех значений х.

Производная от f(x)=F(x), если она существует, называется плотностью (или функцией) распределения вероятностей отказов.

Изучение теоретических законов распределения случайных величин и сфер их пригодности для различных строительных процессов и методов организации строительного производства весьма важно, так как позволяет резко сократить объем статистического материала и продолжительность наблюдений для описания поведения числа и величины отказов.

Равномерное распределение справедливо для тех случаев, когда случайное событие лежит в определенном временном интервале, причем появление его в любой момент времени равновероятно.

Пусть благоприятное событие распределено равномерно на временном интервале Т и плотность распределения постоянна f(x)=const на всем участке действия закона от  до 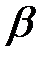. Вероятность события равна 1. Отсюда плотность распределения:

                                                          (2. 6)

Интегральная функция распределения:

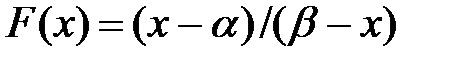                                                     (2. 7)

Математическое ожидание случайной величины, имеющее равномерное распределение:

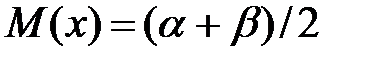                                                              (2. 8)

Дисперсия распределения:

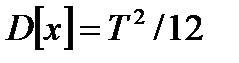 ,                                                                              (2. 9)

т. е. дисперсия равномерного распределения растет пропорционально квадрату интервала, на котором возможно появление отказов процесса.

Показательное распределение является одним из наиболее распространенных в строительном производстве благодаря своей простоте и приблизительному соответствию распределению отказов сложных многоэлементных систем.

Накопление сведений о проведении разнообразных взаимосвязанных строительных процессов деятельности строительно-производственных подразделений приводит к другим законам, более точно отражающим реальное распределение, но одновременно во много раз усложняющим вычисления.

Функция распределения показательного закона записывается следующим образом:

F(x) =                                                                             (2. 10)

Закон справедлив для Х > 0 и зависит только от одном параметра , характеризующего интенсивность (опасность) отказов.

Плотность распределения при показательном распределении:

f(x) = dF(x)/d(x} = ,                                                      (2. 11)

т. е. представляет собой монотонно убывающую функцию.

Математическое ожидание:

                                       (2. 12)    

Дисперсия показательного распределения:

                                  (2. 13) 

т. е. - это свойство показательного распределения можно использовать при оценке возможности его применения для описания экспериментальных данных.

Распределением Вейбулла нередко пользуются при определении надежности ряда процессов. Функция записывается в следующем виде:

                                                      (2. 14)

Это равенство справедливо для х> 0, но зависит от двух параметров  и . При  распределение Вейбулла переходит в показательное.

 

Рис. 2. 1. Законы распределения вероятностей Вейбулла (а), Гаусса (б)

Нормальное распределение широко применяют в теории надежности для описания событий, зависящих от многих факторов, каждый из которых слабо влияет на распределение случайного события. По нормальному закону распределяются параметры выработки исполнителей и бригад на строительных процессах, продолжительности технологических стадий и строительства типовых объектов и др.

Плотность распределения нормального закона записывается в следующем виде:

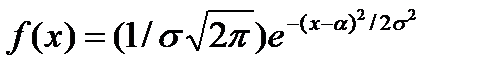,                                               (2. 15)

где - математическое ожидание;

- дисперсия распределения.

Чем больше дисперсия, тем более плоской получается кривая распределения.

Вероятность попадания случайной величины, распределенной по нормальному закону, на заданный интервал измерения параметра х от α до  обычно определяется интегрированием плотности распределения.

Распределение Пуассона наиболее успешно используется для определения вероятности дискретных событий или появления потока событий.

Если независимые события следуют с конкретной средней частотой, то расчет вероятности Р_т, т. е.  вероятности того, что за какой-то отрезок времени t произойдет ровно т событий, производится по закону Пуассона.

Закон Пуассона записывается в следующем виде:

                                                         (2. 16)   

Распределение Пуассона имеет следующее свойство: математическое ожидание и его дисперсия равны одной и той же величине .

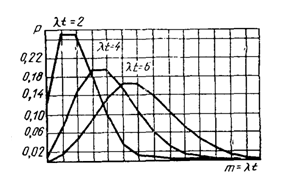
Рис. 2. 2. Закон распределения вероятностей Пуассона

Биноминальным называется такое распределение, при котором его члены получаются в результате разложения бинома (р + q)ⁿ, где р и q - вероятности появления и непоявления события в каждом из п опытов.

Очевидно, что сумма всех членов указанного разложения тождественно равна 1, поскольку (р + q)ⁿ=1 ⁿ, а каждый член разложения представляет собой определенную вероятность, рассчитанную по формуле:

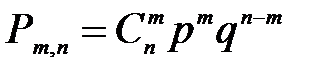,                                                                   (2. 17)

где - число сочетаний из n по m; q = 1 - p.

В лабораторной работе для описания возможных отказов для комплекса работ по балластировки участка пути было принято нормальное распределение, т. к. при производстве работ на данную систему влияет большое количество случайных факторов. Структурная схема надежности приведена на рисунке 2. 3. Значения интенсивности отказов элементов даны в 1/год.

Рис. 2. 3. Исходная схема системы

 λ ₁=λ ₂=λ ₃=λ ₄=λ ₅=0, 35

λ ₆=λ ₇=λ ₈=λ ₉=λ ₁₀=0, 25

λ ₁₁=λ ₁₂=λ ₁₃=λ ₁₄=λ ₁₅=0, 05

λ ₁₆=λ ₁₇=λ ₁₈=λ ₁₉=λ ₂₀=0, 7

λ ₂₁=λ ₂₂=λ ₂₃=λ ₂₄=λ ₂₅=λ ₂₆=λ ₂₇=λ ₂₈=λ ₂₉=0, 55

γ =50%.

 

В исходной схеме все элементы образуют параллельное и последовательное соединение. Заменяем их соответствующими квазиэлементами, получим преобразованную схему системы, рисунок 2. 4 и формулы для расчета надежности всей системы

 

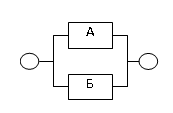
Рис. 2. 4. Преобразованная схема

1) р=1-(1-р_А)(1-р_Б)                                            

2) р_А=р₁р_Вр₆р₇р_Г                                                                                        

3) р_б=р_Др_Ер₂₈р₂₉                                                                           

4) р_В=1-(1-р₂)(1-р₃)(1-р₄)(1-р₅)                         

5) р_Г=1-(1-р_Ж)(1-р_З)(1-р_И)                                

6) р_Д=1-(1-р₁₄)(1-р_К)(1-р_Л)(1-р_М)(1-р₂₁)(1-р_Н)  

7) р_Е=1-(1-р₂₄)(1-р₂₅)(1-р₂₆)(1-р₂₇)                    

8) р_Ж=р₈р₉                                                                                          

9) р_З=р₁₀р₁₁                                                                                                       

10) р_И=р₁₂р₁₃                                                                                   

11) р_К=р₁₅р₁₆                                                                                    

12) р_Л=р₁₇р₁₈                                                                                    

13) р_М=р₁₉р₂₀                                                                                   

14) р_Н=р₂₂р₂₃                                                

Так как по условию все элементы системы работают в периоде нормальной эксплуатации, то вероятность безотказной работы элементов с 1 по 29 подчиняются экспоненциальному закону:

                                                                           (2. 18)

Результаты расчетов вероятностей безотказной работы элементов 1…29 исходной схемы для наработки до 2 лет представлены в таблице 2. 2. 1.

Результаты расчетов вероятностей безотказной работы квазиэлементов по вышеприведенным формулам также представлены в таблице 1.

На рис. 2. 5 представлен график зависимости вероятности безотказной работы системы р от времени (наработки) t.

По графику р на рисунке 2. 2. 5, находим для γ =50% (Р_γ =0, 5) - процентную наработку системы Т_γ =1, 27 года. По условиям задания повышенная                            γ - процентная наработка системы Т'_γ =1, 5Т_γ =1, 905 года.

Таблица 2. 1

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: