Расчет вероятности безотказной работы системы

Элемент	λ, год-1	Наработка t, лет
		0, 1	0, 5			1, 27	1, 905
1-5	0, 35	0, 965605	0, 839457	0, 70468	0, 496585	0, 641145	0, 513374
6-10	0, 25	0, 97531	0, 882497	0, 778801	0, 606531	0, 727967	0, 621108
11-15	0, 05	0, 995012	0, 97531	0, 951229	0, 904837	0, 938474	0, 909146
16-20	0, 7	0, 932394	0, 704688	0, 496585	0, 246597	0, 411067	0, 263553
21-29	0, 55	0, 946485	0, 759572	0, 57695	0, 332871	0, 497331	0, 350726
А	-	0, 918498	0, 652354	0, 420048	0, 162113	0, 328196	0, 178271
Б	-	0, 895827	0, 574908	0, 320881	0, 085418	0, 22926	0, 097703
В	-	0, 999999	0, 999336	0, 992395	0, 935775	0, 983416	0, 943924
Г	-	0, 999986	0, 998497	0, 990295	0, 948301	0, 982238	0, 953621
Д	-		0, 999801	0, 995878	0, 961316	0, 990126	0, 965938
Е	-	0, 999992	0, 996659	0, 967969	0, 801921	0, 936155	0, 82229
Ж	-	0, 951229	0, 778801	0, 606531	0, 367879	0, 529935	0, 385775
З	-	0, 970446	0, 860708	0, 740818	0, 548812	0, 683178	0, 564678
И	-	0, 99005	0, 951229	0, 904837	0, 818731	0, 880734	0, 826546
К	-	0, 927743	0, 687289	0, 472367	0, 22313	0, 385775	0, 239608
Л	-	0, 869358	0, 496585	0, 246597	0, 06081	0, 168976	0, 06946
М	-	0, 869358	0, 496585	0, 246597	0, 06081	0, 168976	0, 06946
Н	-	0, 895834	0, 57695	0, 332871	0, 110803	0, 247338	0, 123009

Продолжение таблицы 2. 1

р	-	0, 99151	0, 852218	0, 606143	0, 233683	0, 482214	0, 258557
Б'	-	0, 963533	0, 827583	0, 664922	0, 366778	0, 57835	0, 391474
28', 29'	0, 1857	0, 981601	0, 91133	0, 830523	0, 689768	0, 789908	0, 702044
р'	-	0, 997028	0, 94006	0, 805671	0, 716734	0, 499957	0, 469432
Б''	-	0, 999685	0, 968955	0, 823532	0, 38108	0, 706405	0, 418986
Р''	-	0, 999974	0, 989207	0, 897657	0, 481415	0, 802762	0, 522564

 

Расчет, представленный в таблице 2. 2. 1, показывает, что при t=1, 905 года для элементов преобразованной схемы, рисунок 2. 2. 4 р_А=0, 178271, р_Б=0, 097703. Следовательно, минимальное значение вероятности безотказной работы имеет элемент Б и именно увеличение его надежности даст максимальное увеличение надежности системы в целом.

В свою очередь элемент Б состоит из последовательно соединенных элементов Д, Е, 28, 29 (р_Д=0, 965938, р_Е=0, 82229, р₂₈=р₂₉=0, 497331). Из них минимальные значения вероятности безотказной работы имеют элементы 28, 29.

Для того, чтобы при Т'_γ =1, 905 года система в целом имела вероятность безотказной работы р_γ =0, 5, необходимо, чтобы элемент Б имел вероятность безотказной работы

Отсюда надежность элементов 28, 29 должна быть равна

P₂₈=р₂₉= 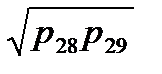=0, 702

Рис. 2. 5. Изменение вероятности безотказной работы исходной системы

   Изменение вероятности безотказной работы исходной системы (р),

                       системы с повышенной надежностью (р')

                       системы со структурным резервированием элементов (р" ).

 

Так как по условиям задания все элементы работают в периоде нормальной эксплуатации и подчиняются экспоненциальному закону (21), то для элементов 28, 29 при t=1, 905 года находим

 

 год .

Таким образом, для увеличения  - процентной наработки системы необходимо увеличить надежность элементов 28 и 29 и снизить интенсивность их отказов с 0, 55 до 0, 1857 год^-1, т. е. в 2, 96 раза.

Для второго способа увеличения вероятности безотказной работы системы - структурного резервирования - по тем же соображениям также выбираем элемент Б, вероятность безотказной работы которого после резервирования должна быть не ниже р" _Б=0, 3915.

Для элемента Б – резервирование означает увеличение общего числа элементов. Аналитически определить минимально необходимое количество элементов невозможно, т. к. число элементов должно быть целым и функция р_Б=f(n) дискретна.

Для повышения надежности системы добавляем к ней элементы, идентичные по надежности исходным элементам 28, 29, до тех пор, пока вероятность безотказной работы квазиэлемента Б не достигнет заданного значения. На первом шаге резервируем элементы 28 и 29 элементами с такой же интенсивностью отказов 28' и 29'.  

р=р_Др_Е(1-(1-р₂₈)(1-р_28'))(1-(1-р₂₉)(1-р_29'))=0, 3967

Так как надежность р=0, 3967< 0, 5 то добавляем еще пару резервных элементов 28" и 29" тогда

р=р_Др_Е(1-(1-р₂₈)(1-р_28')(1-р_28''))(1-(1-р₂₉)(1-р_29')(1-р_29'')=0, 5225

Надежность системы р=0, 5225> 0, 5, следовательно, данная схема удовлетворяет поставленным условиям.

Таким образом, для повышения надежности до требуемого уровня необходимо в исходной схеме, рисунок 2. 3, систему достроить элементами 28', 29', 28'', 29'',

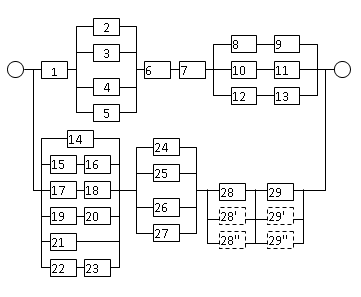
Рис. 2. 6. Структурная схема системы после резервирования

Результаты расчетов вероятностей безотказной работы системы Б'' и системы в целом р'' представлены в таблице 2. 1., а структурная схема после резервирования представлена на рисунке 2. 6.

Расчеты показывают, что при t=1, 905 ч р''=0, 5226> 0, 5, что соответствует условию задания.

На рисунке 2. 5 нанесены кривые зависимостей вероятности безотказной работы системы после повышения надежности элементов 28 и 29 (кривая р') и после структурного резервирования (кривая р" ).

Выводы:

Анализ зависимостей вероятности безотказной работы системы от времени (наработки) показывает, что второй способ повышения надежности системы (структурное резервирование) предпочтительнее первого, так как в период наработки до 1, 905 лет вероятность безотказной работы системы при структурном резервировании (кривая р" ) выше, чем при увеличении надежности элементов (кривая р').

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: