 |
Процессов. расчет абсолютного значения энтропии
|
|
|
|
1. Расчет изменения энтропии при протекании процессов в идеальных газах.
При 
, согласно уравнению Менделеева–Клапейрона 
, тогда изменение энтропии 
моль идеального газа из (21) и (5) равно
.
При 
– 
, тогда из (21) и (6), получим
.
При 
: 
.
2. Расчет изменения энтропии при фазовых переходах (изотермические процессы).
Фазовый переход – процесс, связанный с изменением агрегатного состояния вещества. Данные процессы протекают обратимо и при постоянной температуре.
(22)
3. Расчет изменения энтропии в процессах, связанных с изменением температуры.
При нагревании моль любого вещества от температуры 
до температуры 
при
.
При нагревании моль вещества при
. (23)
В результате интегрирования уравнения в определенных пределах, приняв за нижний предел стандартную температуру 298 
, а за верхний – произвольную температуру 
, получим: (вместо Д должно быть D)
,
где 
– изменение энтропии процесса при температуре ;
– рассчитывают на основании справочных данных о мольных энтропиях индивидуальных веществ (
).
После подстановки значения 
в последнее уравнение и его интегрирования, получим:
.
Для химических реакций справедливо:
.
4.1. Абсолютная энтропия твердых кристаллических тел.
Из (23) получим: 
.
Согласно постулату Планка: энтропия твердого кристаллического тела при абсолютном нуле равна нулю: 
.
Тогда 
.
4.2. Абсолютная энтропия жидкости.
,
где 
– изменение энтропии кристаллического вещества в интервале температур от абсолютного нуля до температуры плавления 
;
– изменение энтропии при плавлении твердого кристаллического вещества;
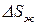– изменение энтропии при нагревании жидкости от до 
.
Подставляем выражения для 
, и :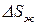
.
4.3. Абсолютная энтропия газа.
|
|
|
,
где 
– изменение энтропии при испарении жидкости;
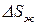– изменение энтропии при нагревании жидкости от до температуры испарения 
;
– изменение энтропии при нагревании газа от до температуры .
Тогда
.
Энтропия и термодинамическая вероятность.
Уравнение больцмана
Состояние системы можно описать либо указав значения температуры, давления, объема и других свойств – это будет характеристика макросостояния системы, либо, указав свойства каждой частицы вещества, то есть ее положение в пространстве, массу, скорость и направление движения – это будет характеристика микросостояния системы.
Если рассмотреть некоторое количество газа с заданными термодинамическими параметрами 
, 
и , то при постоянных внешних условиях макросостояние газа не изменяется, однако молекулы газа находятся в непрерывном хаотическом движении и данному макросостоянию будет отвечать большое число различных микросостояний, которое называется термодинамической вероятностью 
. Величина – есть мера вероятности данного макросостояния: чем больше , тем вероятнее пребывание системы в данном состоянии.
Процессы в изолированной системе направлены в сторону увеличения ее термодинамической вероятности. Равновесное состояние системы – это наиболее вероятное состояние. Как следует из II закона термодинамики, самопроизвольные процессы в изолированной системе характеризуются увеличением ее энтропии. Поэтому можно предположить, что энтропия и термодинамическая вероятность функционально связаны друг с другом. Связь между энтропией и термодинамической вероятностью выражается уравнением Больцмана:
.
Уравнение Больцмана лежит в основе современной статистической термодинамики и позволяет понять свойства энтропии как функции состояния. При абсолютном нуле в системе абсолютный порядок (
) и энтропия 
. При нагревании системы возникает тепловое движение, беспорядок в системе увеличивается и энтропия возрастает. Энтропия – мера беспорядка в системе.
|
|
|
|
|
|
