 |
Понятие о химическом потенциале
|
|
|
|
Выражения I закона термодинамики справедливы при условии неизменности количества составляющих систему веществ, которое определяется числом моль  .
.
Продифференцируем уравнение (27)
 (27)
(27)
 ,
,
выразим из (з) 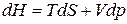 .
.
Решая совместно последние выражения для 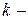 компонентной системы, с учетом изменения числа моль компонентов, участвующих в физико-химическом процессе, получим уравнение для изменения энергии Гиббса системы:
компонентной системы, с учетом изменения числа моль компонентов, участвующих в физико-химическом процессе, получим уравнение для изменения энергии Гиббса системы:
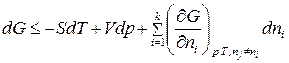 . (1)
. (1)
В (1) знак «<» относится к самопроизвольному процессу, а знак «=» – к равновесному. Частная производная от энергии Гиббса по изменению числа моль одного из компонентов при неизменности чисел моль остальных компонентов и соответствующих параметров состояния – это химический потенциал  го компонента
го компонента  .
.
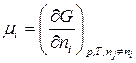 . (2)
. (2)
С учетом (2) получим:
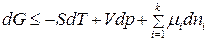 . (3)
. (3)
Химический потенциал можно выразить через частные производные и других термодинамических потенциалов
 (4)
(4)
и аналогично уравнению (1) выразить энергию Гельмгольца  ,
,  ,
, 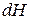 .
.
Химический потенциал размерная величина – 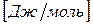 .
.
Химический потенциал имеет физический смысл парциальной мольной работы при изменении числа моль данного компонента на единицу при постоянных внешних параметрах и числах моль всех других компонентов, составляющих раствор.
Для изобарно-изотермических условий, когда  и
и 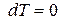 , из (3) при равновесии имеем:
, из (3) при равновесии имеем:
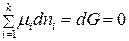 . (5)
. (5)
Для однокомпонентной системы из (5), получим:
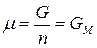 , (6)
, (6)
где  – мольная энергия Гиббса индивидуального вещества или мольный термодинамический потенциал.
– мольная энергия Гиббса индивидуального вещества или мольный термодинамический потенциал.
Таким образом, химический потенциал индивидуального вещества тождественен мольной энергии Гиббса.
Зависимость химического потенциала  го компонента от состава газовой смеси выражается уравнениями:
го компонента от состава газовой смеси выражается уравнениями:
– для идеального газа 
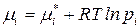 ;
;
|
|
|
– для реального раствора 
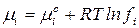 ,
,
где  – парциальное давление
– парциальное давление  го компонента в газовой смеси;
го компонента в газовой смеси;
 – стандартный химический потенциал индивидуального
– стандартный химический потенциал индивидуального  го компонента (
го компонента ( );
);
 – парциальная фугитивность
– парциальная фугитивность  го компонента в газовой смеси;
го компонента в газовой смеси;
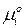 – стандартный химический потенциал
– стандартный химический потенциал  го компонента в газовой смеси (
го компонента в газовой смеси (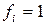 ).
).
Фугитивность (летучесть) – величина, которую нужно подставить в выражение для химического потенциала  го компонента идеальной газовой смеси, чтобы получить значение химического потенциала этого компонента в реальной газовой смеси.
го компонента идеальной газовой смеси, чтобы получить значение химического потенциала этого компонента в реальной газовой смеси.
Фугитивность связана с парциальным давлением компонента уравнением

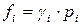 ,
,
где 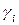 – коэффициент фугитивности
– коэффициент фугитивности  го компонента.
го компонента.
По аналогии зависимость химического потенциала  го компонента от состава жидкого раствора выражается уравнениями:
го компонента от состава жидкого раствора выражается уравнениями:
– для идеального раствора:  ;
;
– для реального раствора:  ,
,
где  – мольная доля
– мольная доля  го компонента в растворе;
го компонента в растворе;
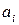 – активность
– активность  го компонента в растворе.
го компонента в растворе.
Активностью  го компонента раствора называют величину, которую нужно подставить в выражение для химического потенциала компонента в идеальном растворе, чтобы получить действительное значение химического потенциала
го компонента раствора называют величину, которую нужно подставить в выражение для химического потенциала компонента в идеальном растворе, чтобы получить действительное значение химического потенциала  го компонента в реальном растворе.
го компонента в реальном растворе.
Активность связана с концентрацией компонента через коэффициент активности  :
:
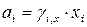 ;
;
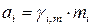 ;
;
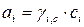 ,
,
где 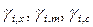 – рациональный, моляльный и молярный коэффициенты активности
– рациональный, моляльный и молярный коэффициенты активности  го компонента в растворе, соответственно;
го компонента в растворе, соответственно;
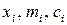 – мольная доля, моляльная и молярная концентрации
– мольная доля, моляльная и молярная концентрации  го компонента в растворе, соответственно.
го компонента в растворе, соответственно.
Между 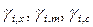 существует вполне определенная взаимосвязь.
существует вполне определенная взаимосвязь.
2.2. Закон действия масс. константа
Химического равновесия
Допустим, что в идеальной газовой фазе протекает химическая реакция:
 ,
,
где 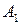 ,
,  , … – исходные вещества:
, … – исходные вещества:
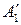 ,
, 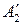 ,… – продукты реакции;
,… – продукты реакции;
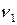 ,
,  ,
,  ,
,  – стехиометрические коэффициенты.
– стехиометрические коэффициенты.
 Условием химического равновесия в системе является равенство
Условием химического равновесия в системе является равенство
 . (7)
. (7)
При химическом равновесии алгебраическая сумма произведений химических потенциалов компонентов на их стехиометрические коэффициенты равна нулю (произведения для продуктов реакции положительны, а для исходных веществ – отрицательны).
|
|
|
Подставив в условие равновесия выражение для химического потенциала: 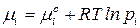 получим уравнение закона действующих масс: при равновесии отношение произведений парциальных давлений продуктов реакции, взятых в степенях их стехиометрических коэффициентов, к аналогичному отношению для исходных веществ, есть величина постоянная при постоянной температуре. Эта величина названа константой химического равновесия:
получим уравнение закона действующих масс: при равновесии отношение произведений парциальных давлений продуктов реакции, взятых в степенях их стехиометрических коэффициентов, к аналогичному отношению для исходных веществ, есть величина постоянная при постоянной температуре. Эта величина названа константой химического равновесия:

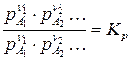 , (8)
, (8)
где 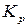 – константа химического равновесия.
– константа химического равновесия.
Константу химического равновесия можно выразить через молярности:



или мольные доли: 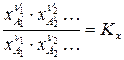

 Константа
Константа 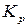 связана с
связана с 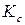 и
и 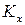 . Подставляя в (8) значения
. Подставляя в (8) значения 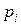 и
и 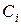 из уравнения Менделеева – Клапейрона
из уравнения Менделеева – Клапейрона 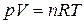 ,
, 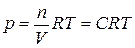 и Дальтона
и Дальтона 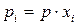 , получим:
, получим:
 ;
; 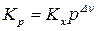 , (9)
, (9)
где  – общее давление в системе;
– общее давление в системе;
 – изменение числа моль в ходе реакции.
– изменение числа моль в ходе реакции.
2.3. уравнение изотермы химической реакции
Направление самопроизвольного протекания химической реакции определяется убылью соответствующего термодинамического потенциала, а глубина протекания – абсолютной величиной этой убыли, т.е. максимальной полезной работой.
Для реакции, протекающей при 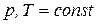 уравнение изотермы химической реакции записывается:
уравнение изотермы химической реакции записывается:

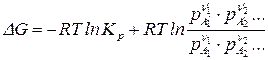 , (10)
, (10)
где 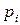 – исходные (неравновесные) парциальные давления реагирующих веществ.
– исходные (неравновесные) парциальные давления реагирующих веществ.
 Так как
Так как  , то уравнение максимальной работы химической реакции запишется:
, то уравнение максимальной работы химической реакции запишется:
 . (11)
. (11)
Аналогично для реакции, протекающей при  :
:

 ;
;

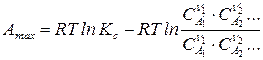 ,
,
где 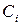 – исходные (неравновесные) концентрации реагирующих веществ.
– исходные (неравновесные) концентрации реагирующих веществ.
Абсолютные значения 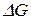 (
(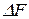 ) показывают, насколько далека система от состояния равновесия. Чем меньше
) показывают, насколько далека система от состояния равновесия. Чем меньше 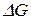 (
(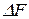 ), тем ближе система к состоянию равновесия. Если
), тем ближе система к состоянию равновесия. Если 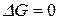 (
(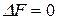 ), то система находится в состоянии равновесия. Поэтому величины
), то система находится в состоянии равновесия. Поэтому величины 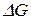 (
(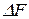 ) или
) или 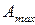 называют мерой химического сродства. На основе уравнения изотермы химической реакции можно предсказать направление самопроизвольного протекания химической реакции: если
называют мерой химического сродства. На основе уравнения изотермы химической реакции можно предсказать направление самопроизвольного протекания химической реакции: если 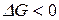 (
( ), то процесс протекает самопроизвольно в сторону образования продуктов реакции, если
), то процесс протекает самопроизвольно в сторону образования продуктов реакции, если  (
(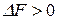 ), то процесс протекает в сторону образования исходных веществ.
), то процесс протекает в сторону образования исходных веществ.
Для приближенной оценки направления протекания химической реакции применяют стандартную энергию Гиббса или стандартное химическое сродство – энергию Гиббса при парциальных давлениях реагирующих веществ, равных единице  :
:
|
|
|

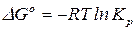 . (12)
. (12)
Аналогично для реакции, протекающей при  :
:

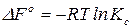 . (13)
. (13)
2.4. уравнения изобары и изохоры химической реакции.
Тепловая теорема нернста-Планка
Влияние температуры на константу химического равновесия характеризуется уравнениями изобары и изохоры химической реакции.
 Если реакция протекает при
Если реакция протекает при 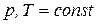 , то
, то
 – уравнение изобары химической реакции. (14)
– уравнение изобары химической реакции. (14)
Если реакция протекает при  , то
, то

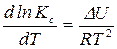 – уравнение изохоры химической реак ции. (15)
– уравнение изохоры химической реак ции. (15)
Уравнения изохоры и изобары позволяют прогнозировать изменение 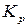 (
(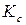 ) при изменении температуры. Знак производной (температурный коэффициент константы равновесия), стоящей в левой части уравнений, а, следовательно, и направление изменения константы равновесия при изменении
) при изменении температуры. Знак производной (температурный коэффициент константы равновесия), стоящей в левой части уравнений, а, следовательно, и направление изменения константы равновесия при изменении  определяется знаком теплового эффекта химической реакции. Если реакция эндотермическая (
определяется знаком теплового эффекта химической реакции. Если реакция эндотермическая (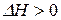 ), то с увеличением температуры
), то с увеличением температуры 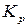 возрастает, если реакция экзотермическая (
возрастает, если реакция экзотермическая ( ), то
), то 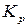 убывает.
убывает.
Основная задача химической термодинамики заключается в расчете константы химического равновесия и определении выхода продуктов реакции.
Разделим переменные в уравнении изобары (14)
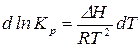 . (16)
. (16)
 Проинтегрируем уравнение в небольшом интервале температур, считая, что
Проинтегрируем уравнение в небольшом интервале температур, считая, что  не зависит от температуры:
не зависит от температуры:
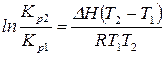 . (17)
. (17)
Уравнение (17) позволяет рассчитать тепловой эффект реакции, если известны значения констант равновесия в узком интервале температур.
|
|
|


