 |
И направление самопроизвольных процессов.
|
|
|
|
Условие термодинамического равновесия в системе
Работа, совершенная системой при протекании обратимого равновесного процесса имеет максимальную величину, по сравнению с работой необратимого неравновесного процесса. Работу обратимого процесса называют максимальной работой:
.
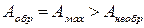Термодинамическими потенциалами называют такие функции состояния, убыль которых в обратимом процессе, протекающем при постоянстве определенных параметров, равна максимальной работе процесса.
Термодинамические потенциалы являются критериями протекания самопроизвольного процесса и равновесия в системе. Для установления вида термодинамических потенциалов воспользуемся объединенным уравнением I и II законов термодинамики, которое получим, приравнивая уравнения:
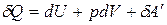и 
. (а)
Для обратимых процессов:
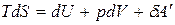. (б)
Для процессов, единственной работой которых является работа расширения, то есть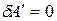 
:
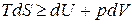, (в)
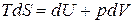. (г)
Так как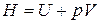 
, то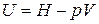 
. Найдем дифференциал 
:
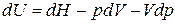
и подставим в уравнения (а) – (г) вместо :
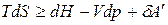, (д)
, (е)
, (ж)
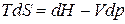. (з)
Применим теперь уравнения (а) – (з) для анализа некоторых процессов.
1.5.1. изохорно-изотермический процесс
Для анализа изохорно-изотермического процесса (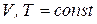
), воспользуемся уравнением (в). При этом получим:
.
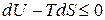Так как Т постоянна, внесем под знак дифференциала и вынесем d за скобки:
.
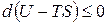Обозначим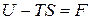 
. (24)
Функция 
стоит под знаком полного дифференциала, то есть ее изменение не зависит от пути процесса, а определяется только исходным и конечным состоянием системы. Кроме того, 
– функция аддитивная, так как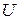 
и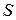 
являются аддитивными функциями, а температура постоянна. Поэтому введенная функция обладает всеми свойствами термодинамической функции состояния. Эту функцию называют функцией Гельмгольца (энергией Гельмгольца, свободной энергией). Таким образом, получаем
|
|
|
, 
.
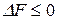Знак < характеризует условие самопроизвольного протекания изохорно-изотермического процесса. Таким условием является убыль энергии Гельмгольца:
, 
.
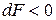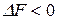Условием равновесия является минимум энергии Гельмгольца:
, 
.
Таким образом, по изменению энергии Гельмгольца можно определить, пойдет или не пойдет процесс и когда наступит равновесие в системе.
Применим уравнение (24) к начальному (1) и конечному (2) состоянию системы в каком-либо процессе, протекающем при :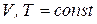
, 
.
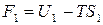Вычтем почленно из последнего уравнения предпоследнее. Получим уравнение Гиббса-Гельмгольца:
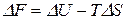. (25)
Таким образом, процесс будет протекать в прямом направлении, если 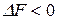, в противоположном направлении, если 
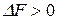, а при 
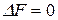система будет находиться в состоянии равновесия.
Для анализа обратимо протекающего изохорно-изотермического процесса применим уравнением (б). Получим:
,
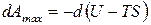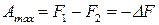. (26)
Как видим, энергия Гельмгольца является изохорно-изотермическим потенциалом, так как ее уменьшение характеризует максимальную работу этого процесса. Максимальная работа изохорно-изотермического обратимого процесса обладает свойствами функции состояния.
1.5.2. изобарно-изотермический процесс
Для анализа процесса, протекающего при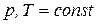 
, воспользуемся уравнением (ж), в результате получим:
.
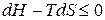Преобразуем: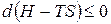 
.
Введем обозначение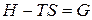 
. (27)
Функция G обладает всеми свойствами термодинамической функции состояния и называется энергией Гиббса (изобарно-изотермическим потенциалом). Таким образом, получаем
, 
.
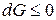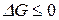Знак < характеризует условие самопроизвольного протекания изобарно-изотер-мического процесса. Как видно, таким условием является убыль энергии Гиббса:
, 
.
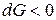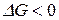Условием равновесия в системе является минимум энергии Гиббса:
, 
.
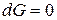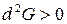Запишем уравнение (27) последовательно для начального (1) и конечного (2) состояния системы при протекании какого-либо изобарно-изотермического процесса:
|
|
|
, 
.
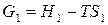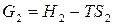Вычтем почленно из последнего уравнения предпоследнее. Получили уравнение Гиббса-Гельмгольца:
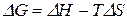. (28)
Уравнение Гиббса-Гельмгольца дает возможность расчета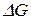 
в любом процессе и определения направления его протекания. Если 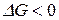процесс идет в прямом направлении, если 
то – в обратном. Если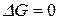 
система находится в состоянии равновесия.
Применим для анализа обратимо протекающего изобарно-изотермического процесса уравнением (е), которое при указанных условиях примет вид:
,
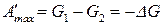. (29)
Как видно, энергия Гиббса в изобарно-изотермическом процессе является термодинамическим потенциалом, т.к. ее убыль равна максимальной работе процесса, а максимальная работа при этом обладает свойствами функции состояния.
2. химическое равновесие
|
|
|
