 |
Лекции, практические занятия
|
|
|
|
Во время сессий для студентов - заочников читаются лекции, проводятся занятия. На лекциях и практических занятиях проводится обзор наиболее важных разделов курса, могут рассматриваться отдельные вопросы программы, отсутствующие или недостаточно полно освященные в рекомендуемых учебных пособиях.
Рекомендации по организации самостоятельной работы студентов
Самостоятельная работа студентов является одним из важнейших элементов обучения. Совершенствование организации самостоятельной работы студентов связано с методической помощью и контролем со стороны преподавателя.
Самостоятельная подготовка должна проводиться по следующими направлениям:
ü изучение теоретического материала, изложенного на лекциях или оставленного для самостоятельной проработки;
ü закрепление навыков выполнения заданий после проведения практических занятий;
ü выполнение контрольных работ;
ü подготовка к зачетам и экзаменам.
Пройденный ранее материал также целесообразно повторить перед следующей лекцией или практическим занятием - это существенно облегчит понимание нового материала, который всегда базируется на уже пройденном.
При самостоятельном изучении дисциплины следует прежде всего изучить литературу по соответствующей теме, обращая внимание на наиболее важные моменты, определяющие понимание соответствующего раздела.
Порядок проведения контроля качества подготовки студентов по дисциплине, содержание контролирующих материалов
Контроль успеваемости и качества подготовки студентов включает текущий контроль, рубежный и промежуточную аттестацию.
Текущий контроль качества подготовки студентов осуществляется в ходе всех видов учебных занятий в форме устного опроса, индивидуальных бесед со студентами.
|
|
|
Рубежный контроль имеет целью установить качество усвоения учебного материала по определенным темам учебной дисциплины. Рубежный контроль проводится в виде контрольной работы, которую студент выполняет самостоятельно, в домашних условиях.
Промежуточная аттестация имеет целью определить степень достижения учебных целей по дисциплине. Промежуточная аттестация проводится в форме обязательной аудиторной контрольной работы.
Методические рекомендации по оформлению и выполнению контрольных работ
Контрольная работа представляет собой работу практического характера. Она должна отражать практическое умение студента решать задачи из курса математики. Подготовка контрольной работы предполагает владение навыками практической работы: умение анализировать задание и формулировать подходы к его решению; подбирать литературу и работать с ней, умение добиться практического результата с помощью стандартного набора средств.
Вариант контрольной работы = списочному номеру в группе (уточняйте у куратора группы). При выполнении контрольной работы надо строго придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студентам для переработки.
1. Контрольные работы выполнять в тетради пастой или чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента. В случае печатной работы – обязательно предоставление электронного варианта работы.
2. На обложке тетради должны быть ясно написаны фамилия студента, его инициалы, название дисциплины; здесь же следует указать дату сдачи работы на проверку.
3. В работу должны быть включены все задачи, указанные в задании, строго по своему варианту. Контрольные работы, содержащие не все задания, а также содержащие задачи не своего варианта, не зачитываются.
|
|
|
4. Решение задач надо располагать в порядке, указанном в заданиях, сохраняя номера задач. Задачи выполняются строго по порядку номеров, записывается полное условие каждого номера, аккуратно и подробно оформляется решение (с пояснениями), формулируется четкий ответ.
5. Перед решением каждой задачи надо выписать полностью её
условие. Если несколько задач имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными из соответствующего номера.
6. После получения отрецензированной работы (как зачтённой,
так и незачтённой) студент должен исправить в ней все отмеченные рецензентом ошибки и недочёты. В связи с этим следует оставлять в конце тетради чистые листы для работы над ошибками. Вносить исправления в сам текст работы после её рецензирования запрещается.
Теоретические и практические основы дисциплины
Тема 1. Дифференциальное исчисление
Определение производной
Определение 2.1: Производной функции  по аргументу x называется предел отношения ее приращения
по аргументу x называется предел отношения ее приращения  к приращению
к приращению  аргумента x, когда приращение аргумента стремится к нулю:
аргумента x, когда приращение аргумента стремится к нулю:
 .
.
Если этот предел конечный, то функция y=f(x) называется дифференцируемой в точке x. Если же этот предел есть ∞, то говорят, что функция y=f(x) имеет в точке x бесконечную производную.
Механический смысл производной: скорость есть первая производная пути по времени, т.е.  .
.
Геометрический смысл производной: тангенс угла наклона касательной к графику функции  равен первой производной этой функции, вычисленной в точке касания, т.е.
равен первой производной этой функции, вычисленной в точке касания, т.е. 
Уравнение касательной к графику функции 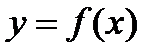 в точке
в точке  :
:
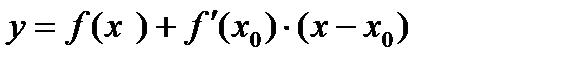
Уравнение нормали к графику функции 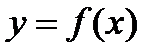 в точке
в точке  :
:

Таблица производных





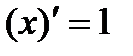





| 





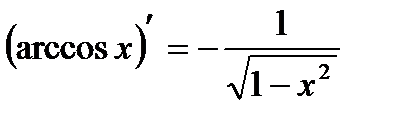


|
Процесс нахождения производных называется дифференцированием функции.
Найти производные функций:
Пример 1: 



 +
+
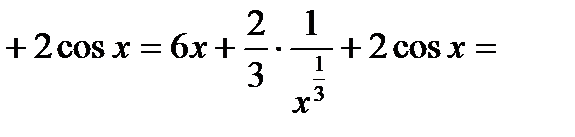

Пример2: 

Пример 3: 


|
|
|


