 |
Применение определенного интеграла при решения некоторых задач по физике и технике.
|
|
|
|
Пусть 
движущегося со скоростью V(t) за время, прошедшее от момента t, до момента t2 вычисляется по формуле
Если материальная точка движется вдоль оси OX под действием силы F(x), зависящей от координаты x, то работа силы по перемещению материальной
точки из «a» в «b» (b>0) вычисляется по формуле:
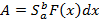
Задачи:
I.Базовый минимальный:
1.Тело движется прямолинейно со скоростью V(t)=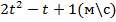 
Найти путь, пройденный за первые 5 секунд.
Указания:
Решение:
Ответ: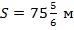 
2.Найти формулу пути, падающего в пустоте, если скорость падения
\с
Указания:
Решение:
Ответ: 
II.Базовый средний:
1.Точка движется по прямой так, что скорость в момент t равна 
. Найти путь, пройденный точкой за время от 3 до 10 секунд.
Указания:
Используй формулу:
Решение:
Ответ: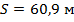 
2. Скорость прямолинейного движущегося тела равна 
. Вычислить путь от начала движения до остановки.
Указания:
В момент остановки тела 
Решение:
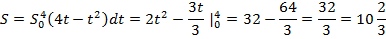
Ответ: 
III.Базовый повышенный:
1.Скорость падающего в пустоте тела определяется по формуле:
V= 9,8 t м\с
Вычислить пройденный путь за первые 10 секунд падения.
Указания:
Решение:
Ответ: 
2.Найти путь, пройденный телом от начала движения до остановки, если скорость его определяется по формуле:
Указания:
Решение:
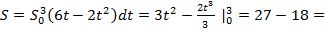9см
Ответ: 
IV.Повышенный уровень:
1.Два тела начинают движение одновременно из одной и той же точки: одно со скоростью 
м\с, другое со скоростью 
. На каком расстоянии они будут через 10 секунд, если они движутся по прямой линии в одном направлении?
Указания:
Решение:
S1 
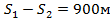
Ответ: 
2.Сила в 1Н растягивает пружину на 3 см. Какую работу она при этом производит?
|
|
|
Указания:
По закону Гука сила пропорциональна растяжению пружины, т.е. сила 
, где 
- величина сжатия или растяжения.
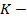коэффициент пропорциональности.
Решение:
Найдем 
1= 
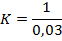
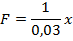
Работа равна:
Ответ: 
Варианты контрольных заданий
Вариант 1.
Задача 1. Найти производные следующих функций:
а) 
. Вычислить 
б) 
в) 
г) 
Задача 2. В какой момент времени скорость тела, движущегося по закону 
равна нулю.
Задача 3. Найдите промежутки монотонности следующих функций
Задача 4. Исследуйте на экстремум следующие функции
Задача 5. Найти следующие интегралы:
а)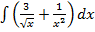 
б) 
в) 
г) 
Задача 6. Фигура, ограниченная прямыми 
и осью Оx, вращается вокруг оси абсцисс. Найти объем полученного тела вращения.
Вариант 2
Задача 1. Найти производные следующих функций:
а) 
.
б)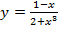 
. Вычислить 
в)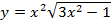 
г) 
Задача 2. Построить график скорости движения тела, заданного уравнениями:
Задача 3. Найдите промежутки монотонности следующих функций
Задача 4. Исследуйте на экстремум следующие функции
Задача 5. Найти следующие интегралы:
а) 
б) 
в) 
г) 
Задача 6. Найти объем тела, полученного вращением части кривой 
отсекаемой осью Оx от ее вершины, вокруг оси абсцисс.
Вариант 3
Задача 1. Найти производные следующих функций:
а) 
.
б) 
в) 
. Вычислить 
г) 
Задача 2. В какой момент времени скорость тела, движущегося по закону 
окажетсяравной 27 ед.
Задача 3. Найдите промежутки монотонности следующих функций
Задача 4. Исследуйте на экстремум следующие функции
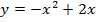
Задача 5. Найти следующие интегралы:
а) 
б) 
в) 
г) 
Задача 6. Фигура, ограниченная прямыми 
вращается вокруг оси абсцисс. Найти объем полученного тела вращения.
Вариант 4
Задача 1. Найти производные следующих функций:
а) 
.
б) 
. Вычислить 
в).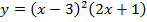 
г) 
Задача 2.Найти уравнение касательной к кривой 
, проходящей через точку с абсциссой, равной -1
Задача 3. Найдите промежутки монотонности следующих функций
|
|
|
Задача 4. Исследуйте на экстремум следующие функции
Задача 5. Найти следующие интегралы:
а)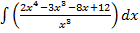 
б)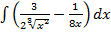 
в)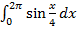 
г)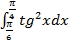 
Задача 6. Фигура, образованная кривой 
и прямыми 
вращается вокруг оси абсцисс. Найти объем полученного тела вращения.
Вариант 5
Задача 1. Найти производные следующих функций:
а) 
.
б) 
в). 
. Вычислить
г) 
Задача 2.Тело движется прямолинейно по закону 
. Определить скорость тела в конце пятой секунды (
). Путь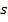 
выражен в метрах
Задача 3. Найдите промежутки монотонности следующих функций
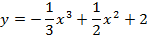
Задача 4. Исследуйте на экстремум следующие функции
Задача 5. Найти следующие интегралы:
а) 
б) 
в) 
г)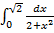 
Задача 6. Фигура, ограниченная кривой 
вращается вокруг оси абсцисс. Найти объем полученного тела вращения.
Вариант 6
Задача 1. Найти производные следующих функций:
а)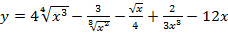 
.
б) 
. Вычислить
в). 
г)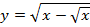 
Задача 2.Найти уравнения касательных к кривой 
, образующих с осью абсцисс угол 135 градусов.
Задача 3. Найдите промежутки монотонности следующих функций
Задача 4. Исследуйте на экстремум следующие функции
Задача 5. Найти следующие интегралы:
а) 
б) 
в) 
г) 
Задача 6. Найти объем тела, поверхность которого образуется вращением кривой 
вокруг оси Oy.
Вариант 7
Задача 1. Найти производные следующих функций:
а) 
.
б) 
.
в) 
Вычислить 
г)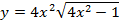 
г)
Задача 2. Построить график скорости движения тела, заданного уравнениями:
Задача 3. Найдите промежутки монотонности следующих функций,
Задача 4. Исследуйте на экстремум следующие функции
Задача 5. Найти следующие интегралы:
а) 
б) 
в) 
г) 
Задача 6. Найти площадь фигуры, ограниченной кривой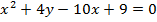 
и прямой 
Вариант 8
Задача 1. Найти производные следующих функций:
а) 
Вычислить
б)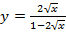 
.
в). 
г) 
Задача 2.Найти уравнения касательных к кривой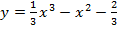 
, параллельных оси Оx.
Задача 3. Найдите промежутки монотонности следующих функций
Задача 4. Исследуйте на экстремум следующие функции
Задача 5. Найти следующие интегралы:
а) 
б) 
в)
г) 
Задача 6. Шар, диаметр которого равен 12 см, рассечен тремя параллельными плоскостями, удаленными друг от друга на расстояния, равные четвертой части его диаметра. Определить объем вырезанного шарового слоя.
|
|
|
Вариант 9
Задача 1. Найти производные следующих функций:
а)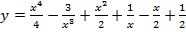 
. Вычислить
б)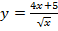 
.
в)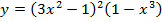 
г) 
г)
Задача 2. Построить график скорости движения тела, заданного уравнениями:
Задача 3. Найдите промежутки монотонности следующих функций
Задача 4. Исследуйте на экстремум следующие функции
Задача 5. Найти следующие интегралы:
а) 
б)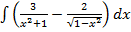 
в) 
г) 
Задача 6. Найти объем шарового сегмента высотой 3 см, отсеченного от шара радиуса 6 см
Вариант 10
Задача 1. Найти производные следующих функций:
а) 
б) 
.
в). 
Вычислить 
г) 
Задача 2. В каких точках кривой 
, надо провести касательную, чтобы она была параллельна прямой 
Задача 3. Найдите промежутки монотонности следующих функций
Задача 4. Исследуйте на экстремум следующие функции
Задача 5. Найти следующие интегралы:
а)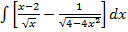 
б)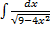 
в) 
г) 
Задача 6. Найти объем тела, поверхность которого образуется вращением дуги окружности 
и прямых 
вокруг оси ОY
Вариант 11
Задача 1. Найти производные следующих функций:
а) 
б) 
Вычислить
в). 
.
г) 
Задача 2.Построить график изменения скорости тела, движущегося по закону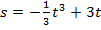 
, на отрезке времени 
Задача 3. Найдите промежутки монотонности следующих функций
Задача 4. Исследуйте на экстремум следующие функции
Задача 5. Найти следующие интегралы:
а) 
б) 
в) 
г) 
Задача 6. Вычислить объем тела, полученного при вращении вокруг оси OYфигуры, ограниченной прямыми 
Вариант 12
Задача 1. Найти производные следующих функций:
а) 
.
б) 
. Вычислить 
в)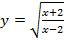 
г) 
Задача 2. Построить график скорости движения тела, заданного уравнениями:
Задача 3. Найдите промежутки монотонности следующих функций
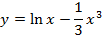
Задача 4. Исследуйте на экстремум следующие функции
Задача 5. Найти следующие интегралы:
а) 
б) 
в) 
г)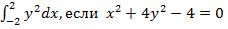 
Задача 6. Площадь фигуры, ограниченной положительными полуосями координат и прямыми 
, равна 48 кв.ед. масшатаба. Определить a(верхний предел интеграла)
Вариант 13
Задача 1. Найти производные следующих функций:
а)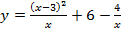 
. Вычислить 
б) 
в). 
.
г) 
Задача 2. В каких точках кривой 
надо провести касательную, чтобы она была параллельна прямой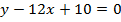 
|
|
|
Задача 3. Найдите промежутки монотонности следующих функций
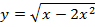
Задача 4. Исследуйте на экстремум следующие функции
Задача 5. Найти следующие интегралы:
а) 
б) 
в)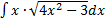 
г) 
Задача 6. Найти объем параболоида, поверхность которого образована вращением дуги параболы 
, заключенной между прямыми 
, вокруг оси Оx.
Вариант 14
Задача 1. Найти производные следующих функций:
а)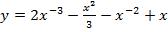 
б) 
. Вычислить 
в). 
г) 
Задача 2. Найти уравнение касательной к кривой 
, параллельной прямой
.
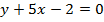Задача 3. Найдите промежутки монотонности следующих функций
Задача 4. Исследуйте на экстремум следующие функции
Задача 5. Найти следующие интегралы:
а) 
б) 
в)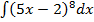 
г) 
Задача 6. Найти площадь, ограниченную прямыми 
.
Вариант 15
Задача 1. Найти производные следующих функций:
а) 
б) 
. 
в). 
. Вычислить
г) 
Задача 2. К кривой 
проведена касательная в точке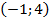 
. Найти уравнение этой касательной.
Задача 3. Найдите промежутки монотонности следующих функций
Задача 4. Исследуйте на экстремум следующие функции
Задача 5. Найти следующие интегралы:
а)
б) 
в) 
г) 
Задача 6. Фигура, ограниченная дугами парабол 
и осью абсцисс, вращается вокруг оси ординат. Найти объем полученного тела вращения
|
|
|
