 |
Общая схема для построения графиков функций
|
|
|
|
1. Найти область определения функции 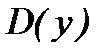 .
.
2. Найти точки пересечения графика функций с осями координат.
3. Исследовать функцию на четность или нечетность.
4. Исследовать функцию на периодичность.
5. Найти промежутки монотонности и точки экстремума функции.
6. Найти промежутки выпуклости и точки перегиба функции.
7. Найти асимптоты функции.
8. По результатам исследования построить график.
Пример: Исследовать функцию и построить ее график:
 .
.
Решение:
1) Функция определена на всей числовой оси, т. е. ее область определения 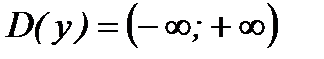 .
.
2) Найдем точки пересечения с осями координат:
с осью ОХ: решим уравнение 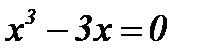
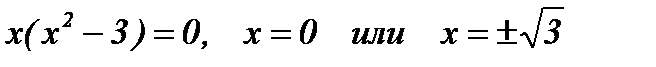 .
.
с осью ОY: 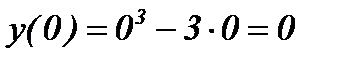
3) Выясним, не является ли функция четной или нечет
ной:
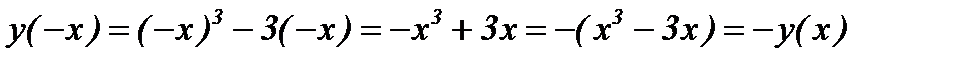 .
.
Отсюда следует, что функция является нечетной.
4) Функция непериодична.
5) Найдем промежутки монотонности и точки экстремума функции: 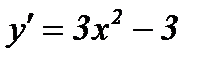 .
.
Критические точки: 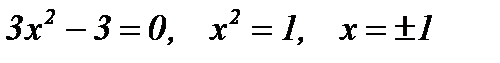 .
.

| 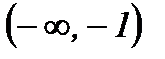
| -1 | 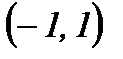
| 1 | 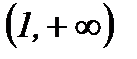
|
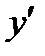
| + | 0 | - | 0 | + |

| т. max | т. min -2 |
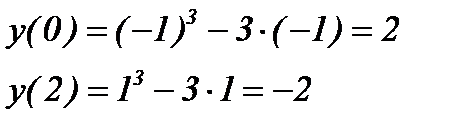
6) Найдем промежутки выпуклости и точки перегиба функции: 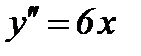
Критические точки: 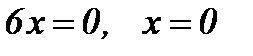 .
.

| 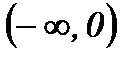
| 0 | 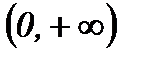
|
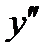
| - | 0 | + |

| точка перегиба |
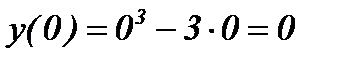
7) Функция непрерывна, асимптот у нее нет.
8) По результатам исследования построим график функции:
y
1 x
-2
Вопросы для самопроверки теме 1. Дифференциальное исчисление:
- Дать определение производной функции.
- Что называется приращением аргумента, приращением функции?
- Какой механический смысл имеет производная?
- Сформулировать геометрический смысл производной.
- Как найти производную суммы или разности?
- Как найти производную произведения?
- Как найти производную частного двух функций?
- Сформулируйте правила нахождения производной сложной функции?
- Как найти производную второго порядка? производную четвертого порядка.
- Что такое критические точки функции?
- Сформулировать достаточные условия возрастания и убывания функции.
- Какими точками отделяются промежутки возрастания от промежутков убывания функции?
- Сформулируйте правила нахождения точек экстремума функции.
- Сформулировать достаточное условие выпуклости функции. Приведите алгоритм нахождения промежутков выпуклости и точек перегиба.
Тема 2. Интегральное исчисление
|
|
|
Неопределенный интеграл. Методы вычисления
Определение 3.1: Функция F(x) называется первообразнойдля функции f(x), если 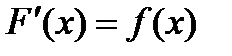 или
или 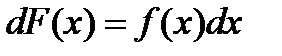 .
.
Любая непрерывная функция f(x) имеет бесконечное множество первообразных, которые отличаются друг от друга постоянным слагаемым.
Определение 3.2: Совокупность F(x)+С всех первообразных для функции f(x) называется неопределенным интегралом от этой функции и обозначается:
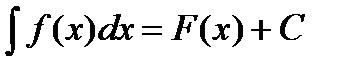 .
.
Основные свойства неопределенного интеграла:
1. 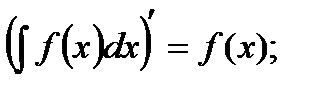 2.
2.  ;
;
3. 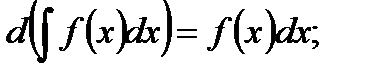 4.
4. 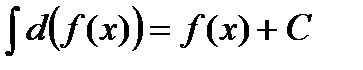 ;
;
5. 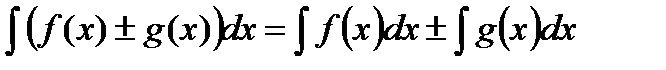 ; 6.
; 6. 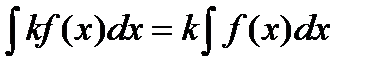 .
.
Непосредственное интегрирование
Непосредственное интегрирование предполагает использование при нахождении неопределенных интегралов таблицы интегралов
Таблица интегралов
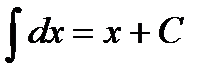

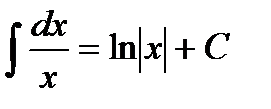
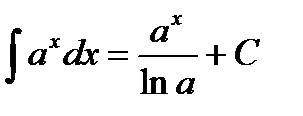
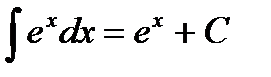
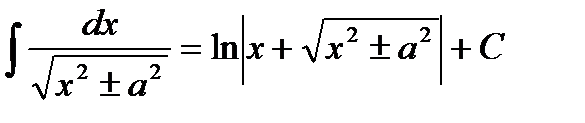

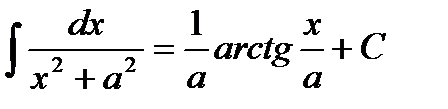 

| 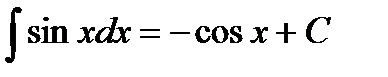
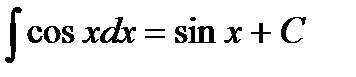

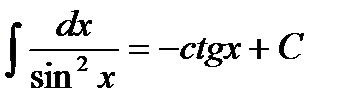
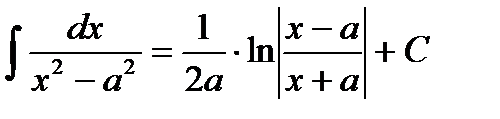
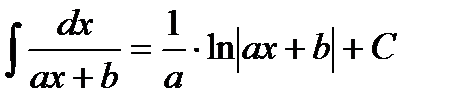

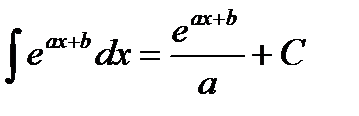 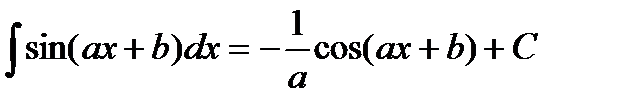 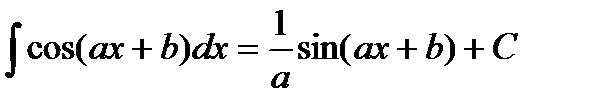
|
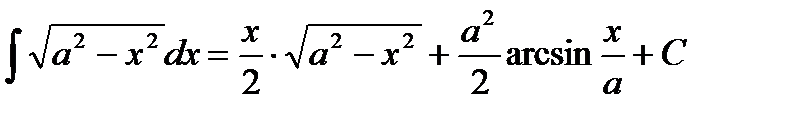
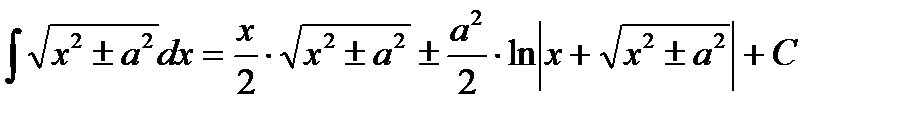
Рассмотрим нахождение интегралов непосредственным методом.
Пример 1: Найти неопределенный интеграл:
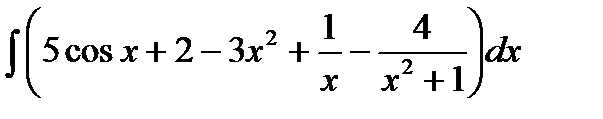 .
.
Решение:  =
=
= 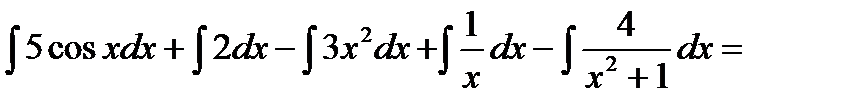


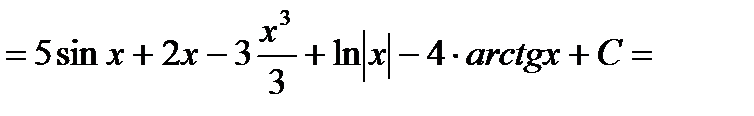
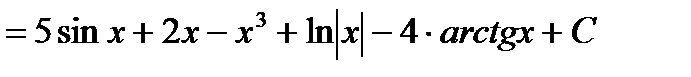 .
.
Пример 2: Найти неопределенный интеграл: 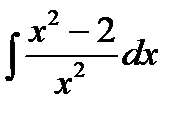 .
.
Решение:  =
= 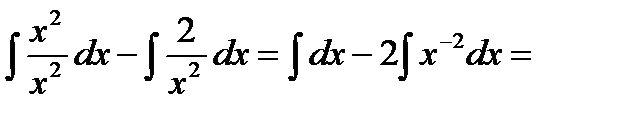

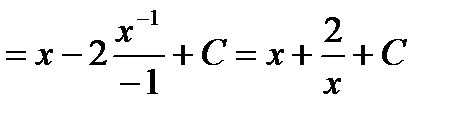 .
.
Пример 3: Найти неопределенный интеграл 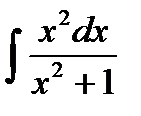
Решение: 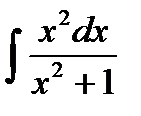 =
= 

Метод подстановки в неопределенном интеграле
(метод замены переменной)
Этот метод заключается в том, что заменяют переменную х на 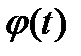 ,где
,где 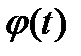 -непрерывно дифференцируемая функция, полагают
-непрерывно дифференцируемая функция, полагают 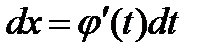 и получают
и получают 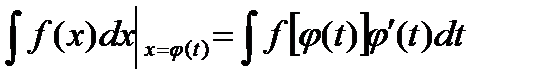
При этом получают искомую функцию, выраженную через переменную t. Для возвращения к переменной х необходимо заменить t значением 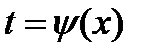 , которое находится из соотношения
, которое находится из соотношения 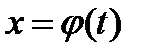 .
.
Рассмотрим нахождение интегралов методом подстановки.
Пример 1: Найти неопределенный интеграл 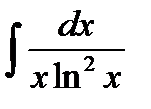
|
|
|
Решение: 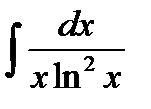 =
= 
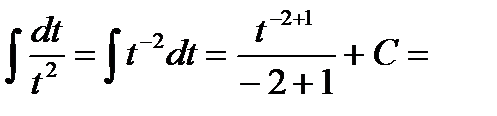

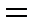
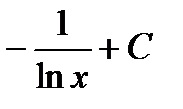

Пример 2: Найти неопределенный интеграл 
Решение: 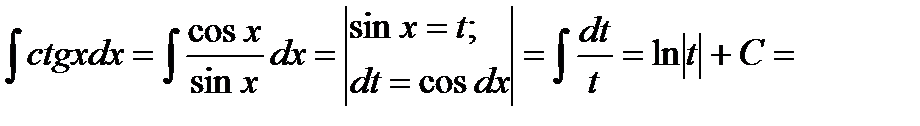
= 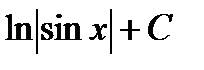
Пример 3: Найти неопределенный интеграл 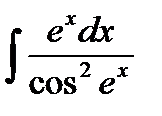
Решение: 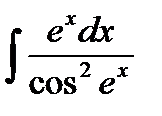 =
= 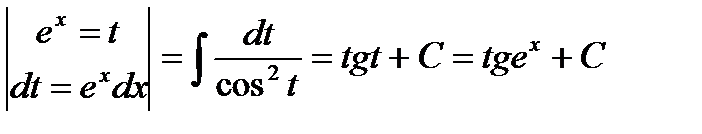
Пример 4: Найти неопределенный интеграл 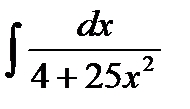
Решение: 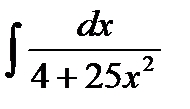 =
= 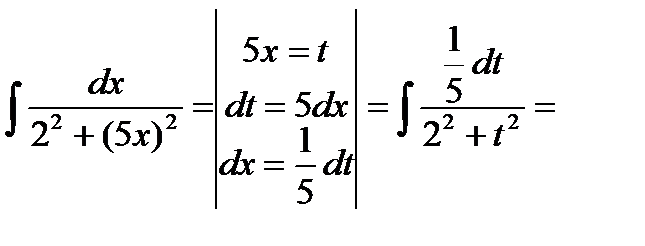
= 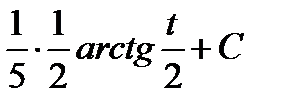 =
=  .
.
|
|
|


