Цепь с активно-индуктивной нагрузкой

ЛАБОРАТОРНАЯ РАБОТА №3

Цепи синусоидального тока с резисторами,

Конденсаторами и катушками индуктивности

1.1.1 Цель работы: ознакомиться с экспериментальными методами определения параметров пассивных приемников в цепях переменного тока. Изучить влияние переменного параметра в ветви цепи на величины и фазы напряжений и токов.

Краткие теоретические и практические сведения

Цепь с активным сопротивлением

Если цепь переменного тока содержит только резистор 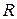(лампа накаливания, электронагревательный прибор и т.д.), к которому приложено синусоидальное напряжение (рисунок 1,а):

,

(1)

то ток в цепи будет определяться значением этого сопротивления:

,

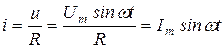(2)

где 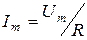– амплитуда тока.

Рисунок 1 – Схема, временная и векторная диаграммы цепи с активным сопротивлением

Из выражений (1) и (2) следует, что в цепи с активным сопротивлением ток и напряжение совпадают по фазе. Обе эти величины можно изобразить на временной (рисунок 1,б) и векторной (рисунок 1,в) диаграммах.

Учитывая, что , , можно записать выражение

,

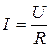(3)

которое называют законом Ома для цепи с активным сопротивлением.

Рассмотрим энергетические процессы в цепи с активным элементом.

Скорость преобразования электрической энергии в другие виды энергии характеризует мгновенную мощность :

,

(4)

где – постоянная составляющая.

График изменения мгновенной мощности для цепи с активным сопротивлением показан на рисунке 1,б. В любой момент времени направления тока и напряжения совпадают, следовательно, мгновенная мощность положительна и колеблется с угловой частотой 2 в пределах от 0 до 2 , т.е. активное сопротивление потребляет электрическую энергию от источника и необратимо преобразует ее в другие виды энергии.

Кроме мгновенного значения мощности , различают еще среднюю мощность за период, которую называют активной мощностью и обозначают буквой :

.

(5)

Активная мощность характеризует работу, совершаемую в электрической цепи за период, т.е. определяет электрическую энергию, необратимо преобразовавшуюся в другие виды энергии. Единицей измерения активной мощности является ватт (Вт).

Цепь с индуктивностью

Пусть по катушке индуктивности , для которой 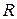=0 (рисунок 2,а), протекает ток

.

(6)

При изменяющемся токе в катушке наводится ЭДС самоиндукции

.

(7)

Приложенное к зажимам цепи напряжение уравновешивает ЭДС самоиндукции

,

(8)

где

,

(9)

называется амплитудой напряжения.

Рисунок 2 – Схема, временная и векторная диаграммы цепи
с идеальным индуктивным элементом.

Таким образом, в цепи с индуктивностью напряжение опережает ток на угол .

Временная и векторная диаграммы изображены на рисунке 2,б и 2,в.

Деля соотношение (9) на , получим:

.

(10)

Здесь имеет размерность сопротивления и называется индуктивным сопротивлением. Выражение (10) называется законом Ома для цепи с индуктивностью.

Перейдем к анализу энергетических процессов в цепи с индуктивным элементом.

Мгновенная мощность индуктивного элемента

,

(11)

изменяется по закону синуса с удвоенной частотой. График мгновенной мощности на индуктивном элементе показан на рисунке 2,б.

В первую четверть периода направления напряжения и тока совпадают и , т.е. индуктивный элемент потребляет электрическую энергию от источника. Во вторую четверть периода направления напряжения и тока противоположны и , т.е. индуктивный элемент является источником и высвобождает энергию, запасенную в магнитном поле.

Активная мощность , характеризующая необратимые преобразования энергии и определяемая средним значением мгновенной мощности за период, для индуктивного элемента равна нулю:

=0.

(12)

Таким образом, в цепи с идеальным индуктивным элементом не совершается работа, а происходит только периодический обмен энергией между источником энергии и магнитным полем. Интенсивность этого обмена принято характеризовать наибольшим значением скорости поступления энергии в магнитное поле, которое называется реактивной мощностью, и обозначают

, вар.

(13)

Реактивная мощность имеет размерность Вольт-Ампер реактивный, сокращенно – ВАр.

Цепь с емкостью

Если цепь переменного тока содержит емкость , к которой приложено синусоидальное напряжение (рисунок 3,а)

,

(14)

то мгновенное значение тока в этой цепи

,

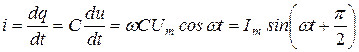(15)

Амплитудные значения тока и напряжения связаны соотношением

.

(16)

Из (15) следует, что ток в цепи с емкостью опережает приложенное напряжение на угол . Временная и векторная диаграммы представлены на рисунке 3,б и 3,в.

Деля соотношение (16) на , получим закон Ома для цепи с емкостью

или ,

(17)

здесь 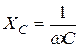имеет размерность сопротивления и называется емкостным сопротивлением.

Рисунок 3 – Схема, временная и векторная диаграммы цепи
с идеальным емкостным элементом.

Перейдем к анализу энергетических процессов в цепи с емкостным элементом. Мгновенная мощность емкостного элемента

,

(18)

изменяется по закону синуса с удвоенной частотой.

График мгновенной мощности приведен на рисунке 3,б. В первую четверть периода направления напряжения и тока совпадают и 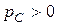, т.е. емкостной элемент потребляет энергию от источника, которая запасается в электрическом поле. Во вторую четверть периода направления напряжения и тока противоположны, , т.е. емкостной элемент является источником и отдает запасенную в электрическом поле энергию.

Активная мощность, характеризующая необратимые процессы преобразования энергии и определяемая средним значением мгновенной мощности за период, для емкостного элемента равна нулю.

=0.

(19)

Таким образом, в цепи с идеальным емкостным элементом не совершается работа, а происходит только периодический обмен энергией между источником и электрическим полем. Интенсивность этого обмена принято характеризовать наибольшим значением скорости поступления энергии в электрическом поле, которое называют реактивной мощностью и обозначают

, ВАр.

(20)

Реактивная мощность емкостного элемента, так же как и реактивная мощность индуктивного элемента, измеряется в Вольт-Амперах реактивных.

 

 

Цепь с активно-индуктивной нагрузкой

Практически любая катушка обладает не только индуктивностью , но и активным сопротивлением 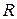(рисунок 4,а).

По второму закону Кирхгофа для мгновенных значений приложенное напряжение к зажимам цепи уравновешивается падением напряжения на активном сопротивлении и падением напряжения на индуктивности:

.

(21)

Выразив напряжения и через ток

(22)

и сопротивления участков цеп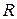и и , получим:

.

(23)

Здесь

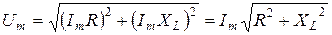,	(24)
.	(25)

Рисунок 4 – Схема, временная и векторная диаграммы цепи с активным сопротивлением и индуктивностью

Таким образом, напряжение на входе цепи с активным сопротивлением и индуктивностью опережает ток на угол 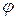. Временная и векторная диаграммы изображены на рисунке 4,б и 4,в.

 

Закон Ома для рассматриваемой цепи на основании (24)

,

(26)

где – полное сопротивление цепи.

Треугольник сопротивлений, подобный треугольнику напряжений, построен на рисунке 5,а. Как видно из этого треугольника

, .

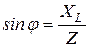(27)

Для анализа энергетических процессов в цепи 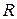, мгновенную мощность удобно представить в виде суммы мгновенных значений активной и реактивной (индуктивной) мощностей 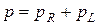. Графики и 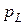изображены на рисунке 5,б.

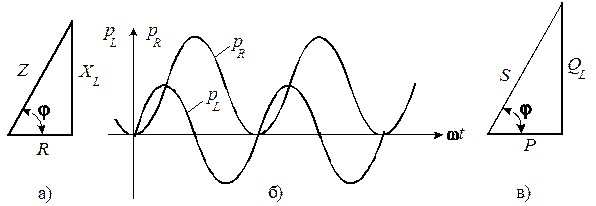Рисунок 5 – Временная диаграмма мгновенных значений активной и индуктивной 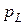мощностей. Треугольники сопротивлений и мощностей

Из графика видно, что активная мощность непрерывно поступает от источника и выделяется в активном сопротивлении в виде тепла. Мгновенная мощность 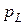непрерывно циркулирует между источником и катушкой.

Умножив стороны треугольника сопротивлений на ток, получим треугольник мощностей (рисунок 5,в).

Стороны треугольника мощностей представляют:

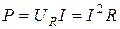– активная мощность цепи, Вт;

– реактивная мощность цепи, ВАр;

– полная мощность цепи, ВА;

– коэффициент мощности цепи.

Параметры реальной катушки (, ) можно определить экспериментально, если последовательно с ней включить дополнительно активное сопротивление 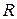(рисунок 6,а).

Измерив ток в цепи, а также напряжения , , 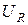, можно построить в масштабе векторную диаграмму в соответствии с рисунком 6,б (т.е. построить косоугольный треугольник по трем известным сторонам).

Тогда

, , .

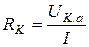(28)

Данный метод определения параметров реальной катушки носит название опыта трех вольтметров.

Рисунок 6 – Электрическая схема и векторная диаграмма цепи с резистором и реальной катушкой индуктивности

Эти параметры также находятся из очевидных уравнений для цепи рисунка 6,а

,	(29)
,	(30)
.	(31)

123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: