 |
Цепь с активно-емкостной нагрузкой
|
|
|
|
Рисунок 7 – Схема, временные диаграммы и треугольники
напряжений, сопротивлений и мощностей цепи
с активным и емкостным элементами
 |
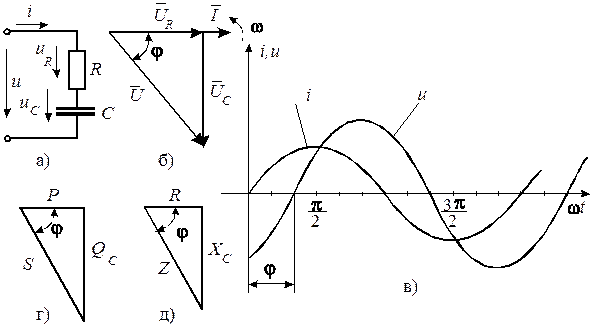В этом случае уравнение напряжения цепи (рисунок 7,а) имеет вид:
 .
| (34) |
Напряжение на активном сопротивлении
 ,
| (35) |
совпадает по фазе с током.
Напряжение на емкости
 ,
| (36) |
отстает по фазе от тока на угол 
.
Таким образом, напряжение 
, приложенное к цепи, будет равно
 ,
| (37) |
На рисунке 7,б изображена векторная диаграмма цепи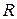 
, 
. Вектор напряжения 
совпадает с вектором тока, вектор 
отстает от вектора тока на угол 90о. Из диаграммы следует, что вектор напряжения, приложенного к цепи, равен геометрической сумме векторов и :
 ,
| (38) |
а его величина
 .
| (39) |
Выразив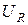 
и 
через ток и сопротивления, получим
 ,
| (40) |
откуда
 .
| (41) |
Последнее выражение представляет собой закон Ома цеп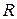и и :
 ,
| (42) |
где 
– полное сопротивление, Ом.
Из векторной диаграммы следует, что напряжение цеп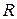и и отстает по фазе от тока на угол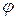 
и его мгновенное значение
 .
| (43) |
Временные диаграммы и 
изображены на рисунке 7,в. Разделив стороны треугольника напряжений (рисунок 7,б) на ток, получим треугольник сопротивлений (7,д), из которого можно определить косинус угла сдвига фаз между током и напряжением:
 .
| (44) |
Энергетические процессы в цепи с активным и емкостным элементами можно рассматривать как совокупность процессов, происходящих отдельно в цеп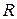и с и с . Из сети непрерывно поступает активная мощность, которая выделяется в активном сопротивлении 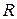в виде тепла. Реактивная мощность, обусловленная электрическим полем емкости , непрерывно циркулирует между источником энергии и цепью. Ее среднее значение за период равно нулю.Умножив стороны треугольника напряжений (рисунок 7,б) на ток, получим треугольник мощностей (рисунок 7,г). Стороны треугольника мощностей представляют:
|
|
|
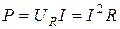– активную мощность цепи, Вт;
– реактивную (емкостную) мощность цепи, ВАр;
– полная мощность цепи, ВА;
– коэффициент мощности цепи.
На основании вышеизложенного можно составить таблицу 1.
Таблица 1 – Пассивные элементы цепей синусоидального тока
| Основные понятия | R | L | C |
Мгновенные значения напряжения и тока
| 
| 
| 
|
Комплексные амплитуды
| 
| 
| 
|
Комплексные действующие значения
| 
| 
| 
|
| Сопротив-ление | 
активное
| 
реактивное индуктивное
| 
реактивное емкостное
|
| Комплексное сопротив-ление | 
| 
| 
|
| Комплексная проводимость | 
| 
| 
|
Экспериментальная часть – опыт 1
Задание
Для цепи с последовательным соединением резистора и конденсатора, а также резистора и индуктивности измерьте потребляемую активную мощность, действующие значения напряжений на резисторе UR и реактивном элементе UC, UL и ток I. Рассчитайте угол сдвига фаз φ, полное сопротивление цепи Z, реактивное сопротивление X и активное сопротивление R, постройте векторную диаграмму.
Порядок выполнения работы
● Соберите цепь согласно схеме (рис. 6.2.4), подсоедините регулируемый источник синусоидального напряжения и установите максимальную амплитуду синусоидального напряжения с частотой f = 1000 Гц.
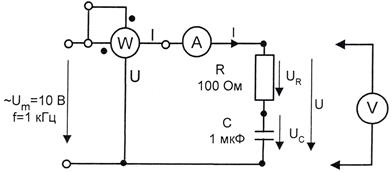
Рис. 6.2.4
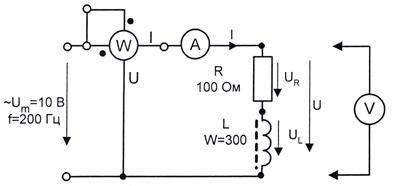
Рис. 6.2.6
Таблица 1 – Результаты измерений и вычислений параметров
катушки и конденсатора методом трех вольтметров
| Цепь | Измерено | Вычислено | ||||||||||
|
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
| |
| В | В | В | В | А | Ом | Ом | Ом | Ом | Гн | Ом | мкФ | |
 ,
| - | - | - | |||||||||
| ,
| - | - | - | - | - |
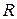Расчетные формулы:
 ;
| 
|
 ;
| 
|
; 
; 
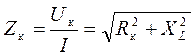
(Значения 
и 
определяем по векторной диаграмме)
ЛАБОРАТОРНАЯ РАБОТА №4
|
|
|
Последовательное соединение конденсатора и катушки индуктивности. Понятие о резонансе напряжений
2.1 Цель работы: изучение явления резонанса напряжений в цепи переменного тока с последовательным соединением 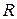, и , приобретение навыков по настройке цепи и по производству измерений, освоение методики и практики вычислений и построения векторных диаграмм по данным измерений.
|
|
|
