 |
Краткие теоретические и практические сведения
|
|
|
|
Если неразветвленную цепь с активным сопротивлением, индуктивностью и емкостью в соответствии с рисунком 14,а присоединить к генератору синусоидального напряжения, то в ней установиться синусоидальный ток.
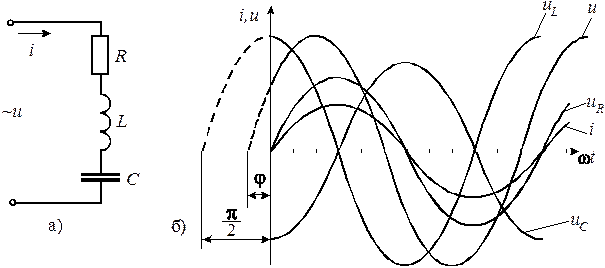
Рисунок 14 – Схема и временные диаграммы тока и напряжений неразветвленной цепи с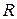 
, 
, 
Выберем начало отсчета времени 
, т.е. примем:
 ,
| (1) |
Напряжение на активном сопротивлении совпадает по фазе с током
 .
| (2) |
Амплитуда этого напряжения 
, а действующее значение 
.
Напряжение на индуктивности или индуктивное напряжение опережает по фазе ток на угол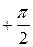 
 .
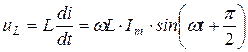| (3) |
Амплитуда этого напряжения 
, а действующее значение 
.
Напряжение на емкости или емкостное напряжение отстает по фазе от тока на угол 
 .
| (4) |
Амплитуда этого напряжения 
, а действующее значение 
.
На рисунке 14,б изображены волновые, а на рисунке 15 векторные диаграммы тока и напряжений рассматриваемой цепи.
Так как элементы цепи 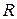, , соединены последовательно, то напряжение на зажимах цепи в любой момент времени равно сумме трех слагаемых:
 .
| (5) |
 |
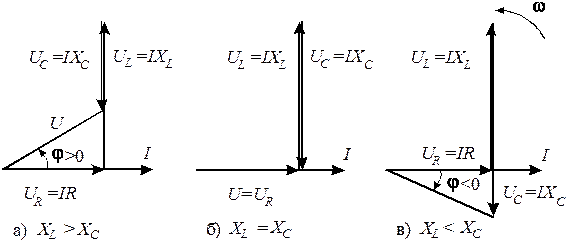Рисунок 15 – Векторные диаграммы тока и напряжений для различных соотношений реактивных сопротивлений
Напряжение на индуктивности и емкости сдвинуты относительно друг друга по фазе на полпериода или на угол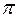 
, их алгебраическая сумма называется реактивным напряжением:
 .
| (6) |
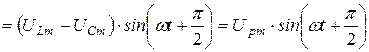
| (7) |
Подставляя в (5) значения 
и 
, получим:
 ,
| (8) |
или
 ,
| (9) |
где
 ;
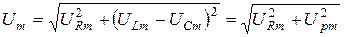| (10) |
 .
| (11) |
Из приведенных уравнений следует, что в общем случае последовательного соединения активного сопротивления, индуктивности и емкости, напряжение на зажимах цепи опережает ток или отстает от него на угол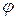 
в зависимости от того, какое из двух напряжений 
или 
больше. Если = , угол 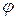=0. Векторные диаграммы напряжений для различных соотношений реактивных сопротивлений приведены на рисунке 15.
|
|
|
Разделив в уравнении (10) все амплитудные величины на 
, получит выражение для действующих значений напряжения:
 .
| (12) |
Подставив в формулу (12) вместо напряжений их выражения через токи и сопротивления, найдем
 .
| (13) |
Здесь
 ,
| (14) |
называется полным сопротивлением цепи.
Выражение (13) называют законом Ома для цепи переменного тока.
При построении векторной диаграммы напряжений за исходный принимается вектор тока. Напряжение на активном сопротивлении совпадает по фазе с током, напряжение на индуктивности опережает ток на угол 
, а напряжение на емкости отстает от тока на угол . Напряжение на входе цепи является геометрической суммой перечисленных напряжений.
Если стороны треугольника напряжений, в соответствии с рисунком 15, разделить на ток, то получим подобный треугольник, катеты которого изображают в определенном масштабе активное 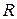и реактивное 
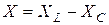сопротивления, а гипотенуза является полным сопротивлением 
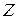(рисунок 16).
Явление, при котором в последовательной цепи из элементов 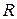, , напряжение на входе цепи совпадает по фазе с током, называют резонансом напряжений.
Условием резонанса служит равенство реактивных сопротивлений
 ,
| (15) |
откуда резонансная угловая частота
 .
| (16) |
Подставляя вместо угловой частоты ее значение, найдем резонансную частоту цепи
 .
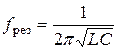| (17) |
При резонансе сопротивление любого из реактивных участков цепи
 ,
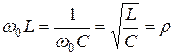| (18) |
принято называть волновым сопротивлением.
 |
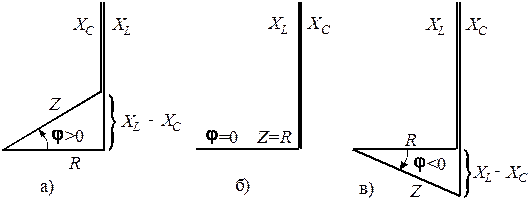Рисунок 16 – Треугольники сопротивлений неразветвленной цепи с
, ,
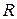Полное сопротивление цепи при резонансе напряжений
 ,
| (19) |
т.е. равно активному сопротивлению цепи и, следовательно, наименьшее из всех возможных при изменении частоты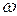 
(рисунок 16,б).
Ток в цепи (действующее значение) при резонансе достигает максимума и совпадает с напряжением по фазе. Таким образом:
|
|
|
 .
| (20) |
При резонансе индуктивное напряжение 
и емкостное 
сдвинуты по фазе на угол 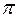и равны по величине; напряжение на зажимах цепи 
равно активному напряжению (рисунок 15,б).
Отношение напряжения на зажимах цепи к напряжению на любом из реактивных участков
 ,
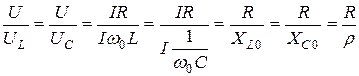| (21) |
откуда
 .
| (22) |
При 
напряжения 
и 
больше приложенного к зажимам цепи напряжения в 
раз. Таким образом, при резонансе напряжений в цепи могут возникать перенапряжения на отдельных участках цепи.
Величина, равная отношению , называется добротностью контура и обозначается буквой 
. Равенство напряжений и при сдвиге фаз на половину периода означает, что в любой момент времени мгновенные напряжения на емкости и индуктивности равны по величине, но противоположны по знаку (
= – 
), следовательно, в любой момент времени равны по величине и противоположны по знаку мгновенные мощности в реактивных участках цепи
 .
| (23) |
Это равенство означает, что накопление энергии в магнитном поле происходит исключительно за счет энергии электрического поля и наоборот, а энергия, поступающая от источника, преобразуется в тепло только в активном сопротивлении.
Настройка цепи в режим резонанса напряжений может быть выполнена по-разному: в цепи с постоянными значениями и , т.е. в цепи с катушкой индуктивности и с постоянным конденсатором, изменением частоты напряжения источника питания до тех пор, пока будет выполняться условие 
. Из выражения 
или 
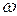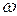следует также, что резонанс можно получить при неизменных и , изменяя индуктивность цепи, или при постоянных и , изменяя емкость цепи (
).
2.3 Экспериментальная часть – опыт 1
Задание
Для цепи с последовательным соединением конденсатора и катушки индуктивности измерьте действующие значения тока I и напряжений U, UC, UL при ω = ω0, ω ‹ ω0 и ω › ω0. Постройте векторные диаграммы.
Порядок выполнения работы
• Соберите цепь согласно схеме (рис. 6.4.5), подсоедините регулируемый источник синусоидального напряжения и установите напряжение на его входе 2 В и минимальную частоту источника В качестве индуктивности используйте катушку 100 мГн и ёмкость в 1 мкФ.
|
|
|
Рис. 6.4.5
Изменяя частоту приложенного напряжения, добейтесь резонанса по максимальному значению тока. Частоту источника питания при максимальном значении тока принимаем как резонансную – f0.
• Произведите измерения и запишите в таблицу результаты измерений при резонансе f=fo при f1 ≈ 0,5f0 и f2≈l,5f0.
Таблица
| f, Гц | I, мА | U, B | UL, B | UC, B |
| f0 = | ||||
| f1 = | ||||
| f 2 = |
•Постройте в одинаковом масштабе векторные диаграммы на рис. 17 для каждого из рассмотренных случаев (см. рисунок 16).
Рисунок 17
|
|
|
