 |
Задание для самостоятельного выполнения.
|
|
|
|
1. С помощью команды Сервис / Свойства обозревателя …/ Конфиденциальность, настройте обозреватель Интернет на вашем компьютере так, чтобы он разрешал использование cookies web - узлам www.google.com и www.google.ru.
2. Зайдите на страницу Настройки Google, задайте и сохраните устраивающие вас параметры настройки. Закройте обозреватель Интернет, снова запустите его, зайдите на сайт Google и убедитесь в том, что ваши настройки действительно сохранились (cookies работают).
3. Повторите поиски по выбранной вами теме из области юриспруденции, создавая соответствующие запросы с помощью страницы расширенного поиска Google, а не специальных синтаксисов.
4. Повторите поиски по выбранной вами теме согласно пункту 3 не на русском, а на английском языке.
5. Используя языковые инструменты Google, переведите на русский язык небольшой фрагмент английского текста, а также какую – либо английскую web – страницу.
6. В отчете по практической работе опишите проделанные вами действия и полученные результаты.
Контрольные вопросы:
1. Чем локальная вычислительная сеть отличается от глобальной?
2. Что такое права доступа в сети? Приведите примеры разграничения прав доступа для различных категорий пользователей.
3. Назовите основные службы сети Internet.
4. Назовите основные цели и задачи создания информационно - вычислительной сети органов внутренних дел.
Литература
1. Гусев, В.С. Поиск в Internet. Самоучитель. – М.: Издательский дом «Вильямс», 2004. – 336 с.: ил.
2. Орлов, А.А. Полная энциклопедия Интернета / А.А. Орлов, Н.В. Богданов – Котьков, А.А. Гор. – М.: АСТ; СПб.: Сова; Владимир: ВКТ, 2008. – 896 с.: ил.
3. Экслер, А. Самый полный и понятный самоучитель работы в Сети, или Укрощение Интернета / А.Б.Экслер. – М.: НТ Пресс, 2007. – 944 с.: ил.
|
|
|
Практическая работа №6. Обработка статистической информации в MS EXCEL
Цель: изучить возможности статистического анализа в MS EXCEL.
Изучив данную тему, студент должен:
иметь представление о
· подходах к анализу статистических данных;
· основных показателях описательной статистики;
знать
· методы обработки результатов статистического наблюдения;
уметь
· использовать инструменты статистического анализа MS Excel;
· использовать инструмент Анализ данных для обработки статистической информации;
владеть навыками
· вычисления статистических показателей с использованием инструмента Пакет анализа MS Excel;
· обработки статистической информации в сфере профессиональной деятельности с помощью компьютерных технологий.
При освоении темы необходимо:
6. Выполнить задание, пользуясь теоретическими сведениями.
7. Оформить выполненное задание в тетради для практических занятий.
8. Результат работы предъявить преподавателю.
9. Ответить на вопросы самоконтроля.
10. Защитить выполненную работу у преподавателя.
Краткая теория по теме:
Вероятностно-статистические методы применяются практически во всех областях науки, в экономике, военном деле, медицине, юридической практике, криминалистике и т.д. Эти методы базируются на понятиях случайного события и вероятности. Вероятность представляет собой количественную характеристику возможности наступления некоторого случайного события.
Случайные величины
В различных задачах могут использоваться величины, значения которых определяются случайным образом. Примерами таких величин являются:
· случайные моменты времени, в которые поступают заказы на фирму;
· время обслуживания клиента в магазине;
· оплата банковских кредитов;
· поступление средств от заказчика;
· ошибки измерений и т.д.
|
|
|
Наиболее распространенными являются следующие распределения вероятности непрерывных случайных величин: равномерное, показательное (экспоненциальное), нормальное, усеченное нормальное, логарифмически нормальное.
Равномерное распределение. Непрерывная случайная величина z, принимающая значения в интервале [ a, b ], имеет равномерное распределение, если ее плотность распределения имеет вид:
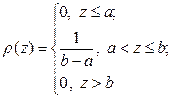
Интегральная функция распределения случайной величины z для равномерного распределения равна:

Числовые характеристики случайной величины z, равномерно распределенной в интервале [ a, b ], имеют следующие значения:
| Математическое ожидание | m z = (a + b)/2 |
| Среднеквадратичное отклонение | 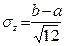
|
Показательное распределение. Непрерывная случайная величина t, принимающая неотрицательные значения в полубесконечном интервале [0, ¥], имеет показательное (экспоненциальное) распределение, если ее плотность распределения вероятности имеет вид:
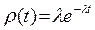
Интегральная функция показательного распределения равна:
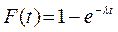
Числовые характеристики показательного распределения определяются по следующим формулам:
| Математическое ожидание | m t = 1/l |
| Дисперсия | D t = 1/l2 |
| Среднеквадратичное отклонение | st = 1/l |
Нормальное распределение. Нормальным называется распределение непрерывной случайной величины y, которая имеет плотность вероятности
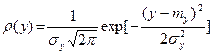
где m y – математическое ожидание случайной величины y; sy – среднее квадратичное отклонение случайной величины y.
Интегральная функция распределения в этом случае определяется по формуле:

Введем нормированную и центрированную случайную величину с нормальным распределением, сделав следующую замену переменной:

Для нормированной и центрированной случайной величины составлена табличная функция Лапласа, имеющая вид[1]:

С помощью табличной функции Лапласа можно определить вероятность попадания случайной величины y в заданный интервал [ a, b ] по формуле:
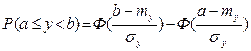
Часто также требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины y по абсолютной величине меньше заданного числа d, т.е. требуется найти вероятность выполнения неравенства | y - m y| < d.
Тогда по предыдущей формуле получим
|
|
|
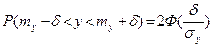
где учтено, что функция Лапласа нечетная.
Усеченное нормальное распределение. Усеченное нормальное распределение случайной величины y задается четырьмя параметрами: математическим ожиданием m y, средним квадратичным отклонением sy, максимальным y 2 и минимальным y 1 значениями (точками усечения). Плотность вероятности такой случайной величины определяется равенством
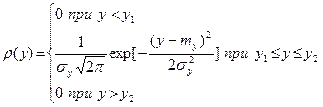
Логарифмически нормальное распределение. В этом случае по нормальному закону распределен логарифм непрерывной случайной величины.
|
|
|


