 |
Показатели анализа динамического ряда
|
|
|
|
СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ЯВЛЕНИЙ
Общие положения. Ряды динамики и их виды
Процессы и явления общественной жизни находятся в постоянном движении и изменении. Поэтому они изучаются при помощи рядов динамики или временных рядов.
Ряд динамики – ряд числовых значений статистического показателя, расположенных в хронологическом порядке и характеризующих изменение явлений во времени. С помощью динамических рядов решают следующие задачи: характеризуют интенсивность развития явления от периода к периоду (от даты к дате) или среднюю интенсивность развития за исследуемый период, выявляют и изучают основную тенденцию в развитии явления, осуществляют прогноз развития на будущее, изучают сезонные колебания.
В каждом ряду динамики имеются два основных элемента: время t и конкретное значение показателя (уровень ряда) y. Уровни ряда могут быть выражены абсолютными, средними или относительными величинами. По времени ряды динамики разделяются на моментные и интервальные.
Моментный ряд динамики – ряд, уровни которого характеризуют состояние явления на определенные моменты времени. Примером такого ряда могут служить данные о численности населения РФ (млн. чел.) по состоянию на 1 января в разные года. Моментные ряды нельзя суммировать, т.к. в каждом последующем уровне полностью или частично содержится значение предыдущего уровня.
Интервальный ряд динамики – ряд, уровни которого характеризуют размер явления за конкретный период времени. Примером такого ряда могут служить данные о динамике добычи нефти в РФ (млн. тонн) за определенный период. Интервальные ряды можно суммировать, т.к. значение предыдущего уровня не содержится в последующем. Это позволяет получать статистические данные за более длительный период времени.
|
|
|
Динамические ряды могут иметь равные или неравные интервалы. Для наглядного изображения явлений в рядах динамики используются диаграммы: столбиковые, ленточные, квадратные, круговые, линейные и др. Выбор вида диаграммы зависит от особенностей исходных данных и цели исследования. Если имеется динамический ряд с несколькими неравноотстоящими уровнями во времени, то используются столбиковые, квадратные или круговые диаграммы. Если число уровней в ряду динамики велико, то применяют линейные диаграммы, которые воспроизводят непрерывность процесса развития в виде ломанной линии. Линейные диаграммы используются так же для изображения общей тенденции и характера развития явления; когда на одном графике необходимо изобразить несколько динамических рядов с целью их сравнения; когда сопоставляются темпы роста, а не значения уровней ряда.
Правила построения рядов динамики
При построении рядов динамики используемые статистические показатели должны быть сопоставимы по:
- территории, что предполагает одни и те же территориальные границы;
- кругу охватываемых объектов, что предполагает сравнение совокупностей с равным числом элементов, однородных по экономическому содержанию;
- времени регистрации, что предполагает для интервальных рядов равенство периодов времени, в течение которого проводятся наблюдения, для моментных рядов – приведение показателей на одну и ту же дату;
- ценам, что предполагает оценивание количества продукции, произведенной в разные периоды, в ценах одного и того же базисного периода;
- методологии расчета;
- единицам измерения, что предполагает выражение показателей в одних и тех же единицах измерения.
Следовательно, прежде чем анализировать ряд динамики, необходимо привести уровни ряда к сопоставимому виду, т.е. произвести смыкание рядов динамики. Под смыканием понимают объединение в один ряд (более длинный) двух или более рядов динамики, уровни которых исчислены, например, по разной методологии или разным территориальным границам. Для осуществления смыкания необходимо, чтобы для периода, в котором произошли изменения (переходного периода), имелись данные как до изменений, так и после изменений. При параллельном анализе развития во времени экономических показателей отдельных стран, административных и территориальных районов ряды динамики приводятся к одному основанию, т.е. к одному и тому же периоду или моменту времени, уровень которого принимается за базу сравнения, а все остальные уровни выражаются в виде коэффициентов или в процентах по отношению к нему.
|
|
|
Показатели анализа динамического ряда
При изучении динамики общественных явлений возникает проблема описания интенсивности изменения и расчета средних показателей динамики.
Анализ интенсивности изменения во времени осуществляется с помощью показателей, получаемых в результате сравнения уровней. К ним относятся: абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процента прироста.
Система средних показателей включает средний уровень ряда, средний абсолютный прирост, средний темп роста, средний темп прироста.
Показатели анализа динамики могут вычисляться на постоянной и переменной базах сравнения. Сравниваемый уровень называется отчетным, уровень, с которым проводится сравнение – базисным.
При расчете показателей на постоянной базе каждый уровень ряда 
сравнивается с одним и тем же базисным уровнем 
, в качестве которого выбирается начальный уровень ряда или уровень, с которого начинается новый этап развития явления. Вычисленные при этом показатели называются базисными.
При расчете показателей на переменной базе каждый последующий уровень ряда сравнивается с предыдущим 
. Вычисленные при этом показатели называются цепными.
Методы расчета показателей динамики приведены в табл. 2.1.
Абсолютный прирост 
характеризует увеличение или уменьшение уровня ряда за определенный промежуток времени.
|
|
|
Коэффициент роста 
характеризует интенсивность, т.е. относительное изменение уровня ряда за определенный промежуток времени. Этот показатель выражается в долях единицы и всегда является положительной величиной.
Темп роста 
- это коэффициент роста, выраженный в процентах.
Темп прироста 
показывает относительную скорость изменения уровня ряда в единицу времени. Этот показатель выражается в процентах и может быть положительным, отрицательным или равным нулю.
Таблица 2.1
Показатели динамики
| Показатель | Метод расчета | |
| С переменной базой (цепные) | С постоянной базой (базисные) | |
|
Абсолютный прирост
| 
| 
|
| ||
|
Коэффициент роста
| 
| 
|
|
Темп роста , %
| 
| 
|
|
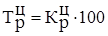
Темп прироста , %
|  ;
 ;
|  ;
 ;
|
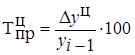
Абсолютное значение 1% прироста 
|  ;
|  ;
|
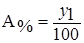
Абсолютное значение 1 % прироста показывает, какое абсолютное значение скрывается за одним процентом прироста и равно сотой части предыдущего (или базисного) уровня. Экономический смысл имеют только значения , рассчитанные на цепной основе.
Методы расчета средних показателей динамики приведены в табл. 2.2.
При написании формул приняты следующие условные обозначения:
n – число уровней ряда;
t – продолжительность периода, в течение которого уровень не изменялся.
Таблица 2.2
Средние показатели динамики
| Показатель | Метод расчета |
Средний уровень ряда  :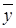
а) для интервального ряда с равноотстоящими уровнями во времени;
| 
|
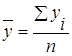
| б) для интервального ряда с неравноотстоящими уровнями; | 
|
| в) для моментного ряда с равноотстоящими уровнями; | 
|
| г) для моментного ряда с неравноотстоящими уровнями | 
|
Средний абсолютный прирост 
|  ; 
|
Средний коэффициент роста 
|   ;
|
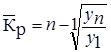
Средний темп роста  , %
| 
|
Средний темп прироста  , %
|  ; 
|
Средняя величина абсолютного значения 1 % прироста 
| 
|
Решение типовых задач
Задание 2. Выполнить анализ динамики производства промышленной продукции в одном из регионов за 1999 – 2005 гг. по условным данным, приведенным в таблице 2.3.
|
|
|
Таблица 2.3
Общий объем промышленной продукции в регионе (млн. руб.)
| Уровни продукции | |||||||
| В старых границах региона | 22,6 | 23,3 | 22,6 | 23,8 | |||
| В новых границах региона | 21,2 | 21,9 | 22,6 | 23,1 |
Для этого
1) определить, какой динамический ряд дан – моментный или интервальный;
2) привести значения уровней двух рядов к сопоставимому виду;
3) рассчитать показатели динамики;
4) для удобства и наглядности исходные и рассчитанные величины представить в виде таблицы;
5) в целом за весь период определить средние показатели динамики;
6) сделать экономический анализ полученных результатов.
Порядок выполнения задания
1) Данный динамический ряд является интервальным рядом (с равноотстоящими уровнями во времени), т.к. приведенные данные характеризуют объем продукции за определенный период (год).
2) Для приведения рядов динамики к сопоставимому виду для 2002 г. определяется коэффициент соотношения уровней двух рядов:
.
Умножая на этот коэффициент уровни первого ряда, получаем их сопоставимость с уровнями второго ряда, млн. руб.:
1999 г.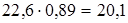 
;
2000 г. 
;
2001 г. 
.
Получен сопоставимый ряд динамики общего объема продукции промышленности в одном из регионов (в новых границах, млн. руб.):
|
| 
| 
| 
| 
| 
| 
|
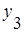
| 20,1 | 20,7 | 21,0 | 21,2 | 21,9 | 22,6 | 23,1 |
3) Рассчитаем показатели динамики, используя формулы из табл. 2.1. В качестве показателя базисного года примем величину объема продукции в 1999 г.
а) абсолютные приросты, млн. руб. (столбцы 2, 3 в табл. 2.4):
| цепные | базисные (1999 г.) |
| 
|
| 
|
 и т.д.
|  и т.д.
|
Отметим, что 
и
.
б) темпы роста (столбцы 4, 5 в табл. 2.4):
| цепные | базисные |
| 
|
| 
|
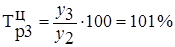
 и т.д.
|  и т.д.
|
Цепные темпы роста производства продукции показывают, что:
- для 2000 г. составил 103 % по сравнению с 1999 г.;
- для 2001 г. составил 101 % по сравнению с 2000 г. и т.д.
Базисные темпы роста производства продукции показывают, что:
- для 2000 г. составил 103 % по сравнению с базисным 1999 г.;
- для 2001 г. составил 104 % по сравнению с базисным и т.д.
в) темпы прироста (столбцы 6, 7 в табл. 2.4):
| цепные | базисные |
| 
|
| 
|
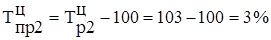
 и т.д.
|  и т.д.
|
Цепные темпы прироста показывают, что производство продукции:
- в 2000 г. возросло на 3 % по сравнению с 1999 г.;
- в 2001 г. возросло на 1 % по сравнению с 2000 г. и т.д.
Базисные темпы прироста показывают, что производство продукции:
- в 2000 г. возросло на 3 % по сравнению с базисным 1999г.;
- в 2001 г. возросло 4 % по сравнению с базисным 1999г. и т.д.
г) цепные абсолютные значения 1 % прироста, млн. руб. (столбцы 8 в табл. 2.4):
|
|
|
; 
;
и т.д.
4) Исходные и рассчитанные показатели динамического ряда представим в табличной форме (табл.2.4).
5) Рассчитаем средние показатели динамики.
а) среднегодовой объем выпуска продукции рассчитывается по формуле средней арифметической простой (табл. 2.2):
млн. руб.
б) среднегодовой абсолютный прирост:
млн. руб.
в) среднегодовой темп роста и темп прироста:
или
,
,
.
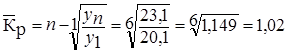Таблица 2.4
Динамика производства промышленной продукции
в одном из регионов за 1999 - 2005 гг
| Год | Выпуск продук-ции, млн. руб. | Абсолютные приросты , млн. руб.
| Темпы роста , %
| Темпы прироста
, %
| Абсо-лютное значение 1 % прироста ,
млн. руб.
| |||
| с пре- дыду- щим годом | с 1999 г. | с пре- дыду- щим годом | с 1999 г. | с пре- дыду- щим годом | с 1999 г. | |||
| А | ||||||||
| 20,1 | - | - | - | - | - | |||
| 20,7 | 0,6 | 0,6 | 0,201 | |||||
| 21,0 | 0,3 | 0,9 | 0,207 | |||||
| 21,2 | 0,2 | 1,1 | 100,9 | 0,9 | 0,210 | |||
| 21,9 | 0,7 | 1,8 | 0,212 | |||||
| 22,6 | 0,7 | 2,5 | 0,219 | |||||
| 23,1 | 0,5 | 3,0 | 0,226 | |||||
| Итого | 150,6 | 3,0 | - | - | - | - | - | - |
г) средняя величина абсолютного значения 1 % прироста:
млн. руб.
6) Экономический анализ полученных результатов.
а) Объем выпуска промышленной продукции в регионе за период с 1999 г. по 2005 г. составил в среднем 21,5 млн. руб.
б) Абсолютные приросты показывают увеличение объема производства по годам (в среднем на 0,5 млн. руб. в год) и по сравнению с базисным 1999 г.
в) Все значения 
. Поэтому можно сделать вывод, что производство промышленной продукции в регионе растет из года в год, хотя и незначительно. Средний темп роста составляет 102 % каждый год.
г) Темпы прироста выпуска продукции за год невелики (в среднем 2 % за год) и остаются практически неизменными на протяжении всего исследуемого периода.
д) Величины показывают, что производство промышленной продукции в регионе в 1999 - 2005 гг. возрастало (в среднем ежегодно на
0,25 млн. руб.).
|
|
|
