Главная | Обратная связь | Поможем написать вашу работу!

Социально-экономических явлений на основе тренда

Аналитическое выравнивание позволяет не только определить общую тенденцию изменения явления на рассматриваемом отрезке времени, но и выполнить расчеты для периодов, для которых нет исходных данных.

Интерполяции - определение недостающих значений признака внутри рассматриваемого периода.

Экстраполяция - определение недостающих значений признака за пределами рассматриваемого периода.

Применение экстраполяции для прогнозирования основывается на предположении, что найденная закономерность развития внутри динамического ряда сохраняется и вне этого ряда. Это справедливо, если исследуемое явление развивается в достаточно стабильных условиях.

Таблица 3.3

Виды трендовых моделей

Наименование функции	Вид функции	Система нормальных уравнений для определения параметров тренда
Линейная
Полином 2–й степени (парабола)
Полином 3–й степени
Показательная
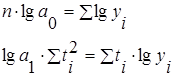
Гиперболическая

Так как анализируемые ряды динамики обычно относительно короткие, то и период экстраполяции не может быть бесконечным. Поэтому срок прогноза – период упреждения (период от конца базы расчета до прогнозируемого периода) не должен превышать длительности базы расчета тренда. На основе динамических рядов получают надежные прогнозы, если уровни ряда сопоставимы и получены по единой методологии.

В отличие от прогноза на основе регрессионного уравнения прогноз по тренду учитывает факторы развития только в неявном виде, что не позволяет «проигрывать» разные варианты прогнозов при разных возможных значениях факторов, влияющих на изучаемый признак. Однако прогноз по тренду охватывает все факторы, в то время как в регрессионную модель невозможно включить в явном виде более 10-20 факторов.

При составлении прогнозов уровней социально-экономических явлений рассчитывают доверительные интервалы прогноза, используя интервальную оценку. Границы интервалов определяют по формуле:

, (3.1)

где – точечный прогноз, рассчитанный по модели тренда на заданную дату;

– коэффициент доверия по распределению Стьюдента (см. тему 1);

– среднее квадратическое отклонение от тренда, скорректированное по числу степеней свободы ;

, – соответственно фактические и расчётные значения уровней динамического ряда;

n – число уровней ряда динамики.

m – число параметров адекватной модели тренда (для линейной функции m = 2, для параболы m = 3 и т.д.).

Величины при различных значениях 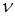приведены в таблице П1 Приложения 1.

Вероятностные границы интервала прогнозируемого явления есть:

. (3.2)

Решение типовых задач

Задание 3. Динамика производства промышленной продукции в одном из регионов за 1999 – 2005 гг. (по условным данным, млн. руб.) приведена в таблице 3.5 (столбцы А и 1).

Используя метод аналитического выравнивания, построить модель тренда, отражающего закономерность развития явления.

Составить интервальный прогноз ожидаемого объема производства продукции в регионе на 2008 г., гарантируя результат с вероятностью 0,95.

Примечание: Исходные и расчетные величины представить в виде таблицы.

Порядок выполнения задания

Таблица 3.4

Исходные и расчетные данные для определения параметров тренда

Год	Объём промышленной продукции , млн. руб.	t
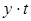
А
	20,1	- 3	- 60,3	20,04	0,06	0,0036
	20,7	- 2	- 41,4	20,53	0,17	0,0289
	21,0	- 1	- 21,0	21,02	- 0,02	0,0004
	21,2			21,51	- 0,31	0,0961
	21,9		21,9	22,00	- 0,1	0,0100
	22,6		45,2	22,49	0,11	0,0121
	23,1		69,3	22,98	0,12	0,0144
Итого	150,6	--	13,7	150,6	--	0,1655

1) Для определения формы тренда проанализируем показатели анализа динамики, рассчитанные в «Задание 2» и представленные в табл. 2.4 (см. тему 2). Из таблицы 2.4 видно, что абсолютные приросты практически постоянны, поэтому в качестве уравнения тренда выбираем линейную функцию: .

Так как количество уровней в ряду динамики нечетное, то временные даты (t) обозначим следующим образом (столбец 2 в табл. 3.4).

2) Система нормальных уравнений для определения параметров и имеет вид (см. табл. 3.3):

откуда получаем: (представляет собой средний

уровень ряда динамики );

Расчет необходимых величин для вычисления и дан в табл. 3.4 (столбцы 3, 4). По итоговым данным определяем параметры уравнения:

, .

В результате получаем следующее уравнение основной тенденции производства промышленной продукции в одном из регионов за 1999 – 2005 гг.:

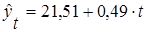. (3.3)

Данное уравнение показывает, что в течение исследуемого периода выпуск промышленной продукции возрастал в среднем на 0,49 млн. руб. в год.

3) Вероятностные границы интервала прогноза объема выпуска продукции в 2008 г. есть:

Для 2008 г. показатель времени t = 6, используя уравнение (3.3), определяем: млн. руб.

При вероятности значение уровня значимости . Для линейной модели тренда число m = 2 и число степеней свободы . По табл. П1 Приложения 1 находим значение коэффициента .