 |
Парная линейная корреляция
|
|
|
|
Простейшей системой корреляционной связи является линейная связь между двумя признаками - парная линейная корреляция. Подобные системы встречаются в тех случаях, когда среди всех действующих факторов выделяется один важнейший, который и определяет вариацию результативного признака, а нелинейные формы связей без особого ущерба могут быть преобразованы в линейные.
Зависимость 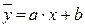 , называется уравнением регрессии y по x или линейной корреляционной зависимостью между y и x.
, называется уравнением регрессии y по x или линейной корреляционной зависимостью между y и x.
где  – среднее значение результативного признака Y при определенном значении факторного признака X;
– среднее значение результативного признака Y при определенном значении факторного признака X;
b – свободный член уравнения;
а – коэффициент регрессии, характеризующий вариацию Y, приходящуюся на единицу вариации X.
Коэффициенты уравнения регрессии рассчитываются по методу наименьших квадратов.
Параметр a определяется из соотношения
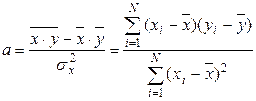 ,
,
где 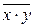 – среднее значение случайной величины x×y;
– среднее значение случайной величины x×y;
 и
и 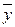 – средние значения факторного и результативного признаков соответственно;
– средние значения факторного и результативного признаков соответственно;
sx – среднее квадратичное отклонение признака X;
xi и yi - индивидуальные значения соответствующих признаков.
Параметр b выражают из уравнения регрессии и вычисляют, подставляя средние значения признаков X и Y и найденное значение параметра а:
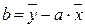 .
.
При парной связи ее теснота измеряется с помощью коэффициента корреляции:

Соотношение между значением модуля коэффициента корреляции и теснотой связи представлено в таблице 4.
Таблица 4
| Значение модуля коэффициента корреляции | Характер связи |
| 0,00 – 0,30 | крайне слабая или отсутствует |
| 0,30 – 0,50 | слабая |
| 0,50 – 0,70 | средняя |
| 0,70 – 0,99 | сильная |
Рассматривая возможные значения коэффициента корреляции, следует учитывать, что нулевая величина этого коэффициента соответствует полному отсутствию какой-либо связи. Это возможно при полном взаимном погашении положительных и отрицательных отклонений признаков от их средних величин. Поскольку вероятность этого крайне мала для любой реальной совокупности, кроме бесконечно большой, то коэффициент корреляции для реальной совокупности отличен от нуля и при отсутствии связи!
|
|
|
Значение коэффициента корреляции, равное 1 (или -1) соответствует функциональной связи. Чем ближе связь к функциональной, тем ближе абсолютная величина коэффициента корреляции к единице. Отрицательное значение коэффициента корреляции свидетельствует об обратной зависимости.
Значение коэффициента корреляции можно посчитать с помощью функции КОРРЕЛ, встроенной в табличном процессоре MS Excel, это облегчит рутинные математические подсчеты. Так же в MS Excel можно построить на графике и эмпирическую ломаную, и уравнение регрессии.
Пример 4. Определение корреляции между числом преступлений, связанных с незаконным оборотом наркотиков, в Новосибирской и Омской областях (данные взяты с официального сайта Федеральной службы государственной статистики РФ www.gks.ru и приведены в таблице 11 (в ед., значение показателя за год)).
Таблица 5.
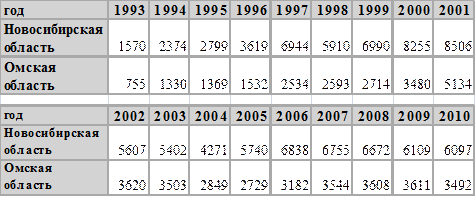
Можно изобразить графически динамические ряды данного вида преступлений в Новосибирской и Омской области (см. рис. 2).
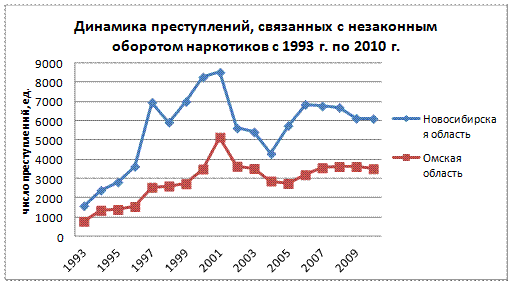
Рис. 2. Динамика преступлений, связанных с незаконным оборотом наркотиков в Новосибирской и Омской областях
Проанализировав график, можно предположить, что эти данные будут коррелировать между собой. Рассчитав коэффициент корреляции, получаем, что 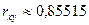 , это означает, что корреляционная связь между признаками прямая и сильная. Изобразим графически эмпирические данные и построим прямую регрессии. Табличный процессор MS Excel позволяет нам автоматически строить прямую регрессии и указывать ее уравнение на диаграмме.
, это означает, что корреляционная связь между признаками прямая и сильная. Изобразим графически эмпирические данные и построим прямую регрессии. Табличный процессор MS Excel позволяет нам автоматически строить прямую регрессии и указывать ее уравнение на диаграмме. 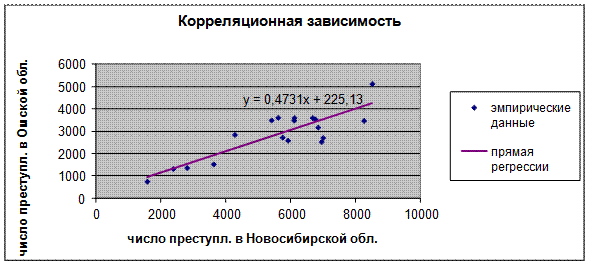 Рис. Рис. 3. Корреляционная зависимость числа преступлений, связанных с незаконным оборотом наркотиков Новосибирской и Омской областях
Рис. Рис. 3. Корреляционная зависимость числа преступлений, связанных с незаконным оборотом наркотиков Новосибирской и Омской областях
|
|
|
|
|
|


