 |
Антагонистическая игра с полной информацией
|
|
|
|
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ.. 4
1. ПРЕДМЕТ, ЗАДАЧИ ТЕОРИИ ИГР. КЛАССИФИКАЦИИ ИГР.. 6
1.1. Предмет, задачи теории игр. 6
1.2. Классификации игр. 13
1.3. Постановка задачи. 15
2. Антагонистические игры... 21
2.1. Основы теории. 21
2.2. Антагонистическая игра с полной информацией. 25
2.3. Антагонистическая игра без информации. Смешанные стратегии. 33
3. Многошаговые игры... 42
3.1. Основы теории. 42
3.2. Многошаговые (позиционные) игры с полной информацией. 47
3.3 Игра с выжиданием.. 49
4. Неантагонистические (биматричные) игры... 56
4.1. Бескоалиционная игра в нормальной форме. 56
4.2. Биматричные игры. Основы теории. 57
4.3. Решение биматричной игры.. 63
6. БЕСКОАЛИЦИОННЫЕ ИГРЫ... 95
6.1. Основы теории. 95
6.2. Задача, касающаяся рекламы.. 97
6.3. Диадические игры. Пример: экологический конфликт. 104
6.4. Пример. Справедливое распределение штрафа. 112
Постановка задачи
Продукты или услуги, предлагаемые компаниями на рынке, можно сравнивать и упорядочивать не только по таким объективным характеристикам, как, например, цена, качество и тому подобное, по их популярности, по тому, какой предпочтительнее. Компании, учитывая предпочтения покупателей, предлагают свои продукты или услуги в соответствии с требованиями рынка. При этом различные группы потребителей в отношении одних и тех же продуктов или изделий могут иметь различные предпочтения.
Исследуем компании, упорядочивающие по степени важности для их бизнеса предлагаемые четыре вида камер: камеры для ведения съемки первого вида К1 (направленности, например, для малых предприятий), камеры для ведения съемки второго вида (К2),камеры для управления складскими запасами первого вида (КС1) и камеры для управления складскими запасами второго вида (КС2). Предположим, что по данным проведенного обследования некоторый контингент потенциальных клиентов оказался разделенным на четыре группы, установившие порядки предпочтения, описываемые таблицей 1.1.
|
|
|
Таблица 1.1
| Номер группы | Предпочтительность по порядку для группы |
| КС2, К2, КС1, К1 К2, КС1, К1, КС2 КС1, К1, КС2, К2 К1, КС2, К2, КС1 |
Пусть при этом оказалось, что группы потенциальных покупателей, придерживающихся порядков предпочтения 1, 2, 3 и 4, составляют соответственно 15, 10, 50 и 40 процентов от общего числа покупателей, а покупатели, выбравшие иные порядки предпочтения, отсутствуют. (Подчеркнем, что эти предположения составляют условия задачи, и будем соблюдать их при ее решении.)
Можно ли в описанных условиях устанавливать какое-либо разумное упорядочение по предпочтению для рассматриваемого нами контингента покупателей в целом? Можно ли хотя бы выбрать камеры, разработка которых удовлетворила бы покупателей в наибольшей степени?
Пусть проведено голосование «на лучшие камеры» (по функциональности для конкретного пользователя, цене, пользовательскому интерфейсу и т. д.). По правилу относительного большинства перевес, очевидно, даст К1, которое соберет 40 % голосов. Ближайший конкурент, КСО1, соберет лишь 30 % голосов.
Однако сторонники КСО1 могут поставить на голосование вопрос: какое программное обеспечение из двух лучше, КО1 или КСО1? Из табл. 1.1 порядков видно, что за КСО1 при сравнении с КО1 будут голосовать 1, 2 и 3-я группы, и всего за это программное обеспечение будет подано 60 % голосов против 40 %, поданных за БПО1. Далее нам понадобится рассматривать различные голосования такого типа, поэтому для удобства читателей мы вычислим впрок результаты и сведем их в «турнирную» таблицу 1.2.
Таблица 1.2
| К1 | КС1 | К2 | КС2 | |
| К1 | х | 25% | 75% | 85% |
| КС1 | 75% | х | 50% | 60% |
| К2 | 25% | 50% | х | 10% |
| КС2 | 15% | 40% | 90% | х |
|
|
|
Например, сравнивая К2 и КС2, видно, что К2 отдают предпочтение 90% потребителей, однако остальные две группы предпочитают КС2, соответственно 10% отдают предпочтение КС2. Остальные сравнения проводятся по аналогии.
Антагонистические игры
Антагонистическая игра с полной информацией
В игре участвуют два игрока – Сокол и Чайка, а выигрыш определяется количеством оказанных услуг.
Предположим, что компания Чайка заранее знает стратегию, с которой планирует работать компания Сокол и с связи с этим принимает решение о своих действиях. То есть компания Чайка после выбора стратегии своего соперника не сможет изменить свою. Сокол может придерживаться одного из двух направлений: отдать предпочтение К1 или К2. Соответственно Чайка также имеет два состояния: информация о выборе компании Чайка направления К1 или К2.
Основываясь на этих выводах, составляется матрица стратегий.
Таблица 2.2
| Стратегии предприятия «Сокол» Стратегии предприятия «Чайка» | К1→ КС1 К 2→ КС1 | К1→ КС1 К 2→ КС 2 | К1→ КС 2 К 2→ КС1 | К1→ КС2 К 2→ КС2 |
| К1 | К1→ КС1 25:75 | К1→ КС1 25:75 | К1→ КС 2 85:15 | К1→ КС2 85:15 |
| К2 | К 2→ КС1 50:50 | К 2→ КС 2 10:90 | К 2→ КС 2 10:90 | К 2→ КС 2 10:90 |
После подобных упрощений наша таблица приобретает вид:
 | 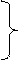 | ||



 25 25 85 85
25 25 85 85
50 10 10 10 (2.8)
Находим maxmin и minmax:
 | 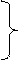 | 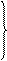 | |||
25 25 85 85 25 α maxmin= 25
50 10 10 10 10
50 25 85 85
minmax = 25
Итак, α = β = 25 – седловая точка в чистых стратегиях. Это говорит о том, что фирме Сокол нужно выбрать первую стратегию, т.е. заниматься камерами первого типа, а фирме Интерком также выбрать первую стратегию и заниматься камерами первого типа, чтобы занять 85% рынка.
|
|
|


