 |
Неантагонистические (биматричные)
|
|
|
|
Решение биматричной игры
| Стратегии предприятия «Сокол» Стратегии предприятия «Чайка» | К1→ КС1 К 2→ КС1 | К1→ КС1 К 2→ КС 2 | К1→ КС 2 К 2→ КС1 | К1→ КС2 К 2→ КС2 |
| К1 | К1→ КС1 25:75 | К1→ КС1 25:75 | К1→ КС 2 85:15 | К1→ КС2 85:15 |
| К2 | К 2→ КС1 50:50 | К 2→ КС 2 10:90 | К 2→ КС 2 10:90 | К 2→ КС 2 10:90 |
Предположим, что конъюнктура на рынке изменилась, и возможности сбыта возросли следующим образом. Согласно исследованиям маркетологов, просматривается тенденция оказания услуг в комплексе (интернет и телефония). Можно предполагать, что из тысячи рассматриваемых покупателей в случае появления на рынке услуг в комплексе 50 % приобретут обе эти системы, а остальной спрос распределится согласно данным табл. 2, а дополнительно будет продано 275 и 225.
250 350 150 380
500 100 475 375 
(4.3)
В таком случае выигрыш первого игрока равен:
250pq + 500(1-p)q + 350p(1-q) + 100 (1-p)(1-q)
H(p,q) = 100-500pq +400pq+250p
Если 1 игрок заменит стратегию на чистую, т.е. p = 0;1, тогда:
H(p,q) > H(1,q) = 150-100q
H(p,q) > H(0,q) = 100 + 400q
Приравняем:
150-100q = 100 + 400q
q = 0.1; (1-q) = 0.9
Выигрыш второго игрока равен:
150pq + 475 (1-p)q + 380p(1-q) + 375 (1-p)(1-q)
H(p,q) = -330pq +100q +5p + 375
Если 2 игрок заменит стратегию на чистую, т.е. q = 0;1, тогда:
H(p,q) > H(p,1) = 475-225p
H(p,q) ≥ H(p,0) = 5p+375
Приравняем:
475-225p = 5p+375
p =0.4; (1-p) = 0.6
Рассматриваемая игра имеет только одну ситуацию равновесия, которая состоит из стратегии (0.1; 0.9) игрока 1 и стратегии (0,4; 0,6) игрока 2.
БЕСКОАЛИЦИОННЫЕ ИГРЫ
Игры в нормальной форме с тремя и более игроками требуют более сложного анализа, чем игры с двумя игроками.
Рассмотрим следующую задачу, с которой могут встретиться наши три предприятия: «Чайка», «Сокол» и «Утро». Предположим, что каждое из них разрабатывает по одному виду ПО. Среди других способов рекламы своих продуктов предприятия могут воспользоваться рекламой на телевидении. Рассмотрим, к примеру, возможность демонстрации рекламного ролика вечером (в prime time) либо утром. Далее будем касаться лишь эффективности этих видов рекламы и притом применительно к контингенту тех покупателей, которые смотрят вечерние телепередачи в среднем вдвое чаще, чем утренние. Кроме того, потенциальные клиенты, увидев в одном рекламном ролике продукты двух конкурирующих предприятий, не склонятся к покупке ни одного из них, т. е. таким образом мы сформулируем условие задачи.
|
|
|
|
|
Таким образом, с одной стороны, каждое предприятие заинтересовано в вечерней рекламе (ибо она по сравнению с утренней завербует большее число покупателей), а с другой – в том, чтобы не участвовать одновременно с другим предприятием в одном рекламном ролике (ибо тогда оба одновременно участвующие в рекламе предприятия только дезориентируют покупателей и реклама останется без ответа). Обратим внимание на то, что здесь для каждого предприятия в отдельности имеется объективно наилучший способ действий: реклама на телеканале вечером. Однако как только этот способ действий избирает более чем одно предприятие, он уже становится бесполезным.
|
Хочется еще раз отметить, что существуют условия задачи и то, ЧТО не предусмотрено в условиях задачи, не должно использоваться в ее решении. В частности, условия задачи не предусматривают получения от телеканалов информации, например, об уже поступивших заказах на рекламу. Равным образом мы имеем в виду вполне определенных покупателей выпускаемого товара.
Формализуем поставленную задачу, представив ее как игру в нормальной форме.
Участниками игры (игроками) являются здесь предприятия, которые мы для удобства обозначим через 1, 2 и 3. Напротив, ни покупатели, ни телевидение, хотя их интересы прямо или косвенно и отражены в условиях данной задачи, не действуют в условиях задачи вполне определенным образом и поэтому игроками считаться не могут.
|
|
|
Каждый игрок имеет в данном случае две стратегии: участвовать в утренней рекламной передаче (стратегия 1) и в вечерней (стратегия 2), поэтому в игре имеется 
ситуаций. На основании имеющегося опыта мы можем предвидеть, что в данной игре придется рассматривать также смешанные стратегии игроков и составлять из них ситуации. Введем эти понятия уже сейчас, до того как в этом возникла непосредственная необходимость.
Смешанная стратегия каждого игрока состоит в случайном выборе его стратегий 1 или 2. Обозначим через p 1 вероятность выбора игроком 1 его первой чистой стратегии. Очевидно, p 1 может принимать любое значение от 0 до 1. При этом p 1= 1 соответствует случаю, когда игрок 1 выбирает свою первую чистую стратегию с вероятностью 1, а p 1= 0 – случаю, когда он выбирает первую чистую стратегию с вероятностью 0 (т. е. на самом деле выбирает вторую чистую стратегию).
Аналогично через р 2 обозначим вероятность выбора первой чистой стратегии игроком 2, а через р 3 – вероятность выбора первой стратегии игроком 3.
Ситуациями в смешанных стратегиях будут всевозможные комбинации смешанных стратегий игроков, т. е тройки вида
, где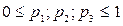 
. (6.4)
Очевидно что ситуациям в чистых стратегиях соответствуют тройки, состоящие из нулей и единиц, и только они.
Как известно, множество всех троек вида (6.4) естественно описать как «единичный» куб в системе координат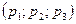 
(рис. 6.1). В этом описании ситуации в чистых стратегиях соответствуют вершинам куба.
Рис. 6.1
Перейдем к условиям игры:
P = 1 (утро)
P= 0 (вечер)
Более одного, то V = 0
p 1 = 1 стратегия V = 5
p 0= 2 стратегия V = 7
1 игрок:
5 p 1 (1- p 2) (1- p 3) + 7 (1- p 1) p 2 p 3
2 игрок:
p 1 * 7(1- p 2) p 3 + (1- p 1)5 p 2 (1- p 3)
3 игрок:
(1- p 1) (1- p 2)5 p 3+ p 1 p 2 * 7(1- p 3)
Преобразуем:
1 игрок:
P1=1;
5 p 1 (1- p 2) (1- p 3) + 7 (1- p 1) p 2 p 3 ≥ 5 (1- p 2) (1- p 3) + p 2 p 3;
P1=0;
5 p 1 (1- p 2) (1- p 3) + 7 (1- p 1) p 2 p 3 ≥ 7 p 2 p 3;
2 игрок:
P1=1;
p 1 * 7(1- p 2) p 3 + (1- p 1)5 p 2 (1- p 3) ≥ 7 - 7 p 2 p 3;
P1=0;
p 1 * 7(1- p 2) p 3 + (1- p 1)5 p 2 (1- p 3) ≥ 5 p 2 - 5 p 2 p 3;
|
|
|
3 игрок:
P1=1;
(1-p1) (1- p2)5p3+ p1 p2 * 7(1- p3) ≥ 7 p 2 (1- p 3)
P1=0;
(1-p1) (1- p2)5p3+ p1 p2 * 7(1- p3) ≥ 5 p 3 (1- p 2)
|
|
|
