 |
Антагонистическая игра без информации. Смешанные стратегии
|
|
|
|
Предположим, компании занимаются решением аналогичной задачи (рассмотренной в предыдущем разделе) с тем, однако, единственным отличием, что не только «Чайка» узнает о продукции предприятия «Сокол» после выбора ею своего вида камер, но и «Сокол» не может получить предварительной информации и вынуждено принимать свое решение, не зная о решении предприятия «Чайка». Таким образом, в этом случае как «Чайка», так и «Сокол» имеют по одному информационному состоянию. В своем единственном информационном состоянии каждое из предприятий имеет две альтернативы: выпускать первый вариант камер или второй его вариант. Эти альтернативы и будут стратегиями наших игроков.
Полученная игра является матричной, имеет  ситуации, и матрицей выигрышей в ней, очевидно, будет:
ситуации, и матрицей выигрышей в ней, очевидно, будет:
| КС1 | 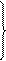 КС22 КС22
| |||
| К1 | 25 25 25 | ||||
| К2 | 10 10 |
α maxmin= 25
β minmax = 25
50 25 2.11
Итак, α = β = 25 – седловая точка в смешанных стратегиях. Это значит, что фирма Чайка должна выходить на рынок с камерами первого типа, таким образом она займет 25% рынка, а фирме Сокол придется работать с камерами второго типа, что позволит ей занять 75%.
Предположим, что исходные данные привели бы к другому решению задачи:
 7 6
7 6
2 7
Где:
p – вероятность выбора 1-ым игроком стратегии 1;
(1-p) – вероятность выбора 1-ым игроком стратегии 2;
q – вероятность выбора 2-ым игроком стратегии 1;
(1-q) - вероятность выбора 2-ым игроком стратегии 2;
Тогда ожидаемый выигрыш игрока 1 при условии, что игрок 2 выберет 1 столбец матрицы:
7*p + 2*(1-p) = 5*p + 2 (1)
Oжидаемый выигрыш игрока 1 при условии, что игрок 2 выберет 2 столбец матрицы:
6*p + 7*(1-p) = 7 - p (2)
При независимом выборе игроков, т.е. если игрок 1 выбирает стратегию с вероятностью q он желает получить выигрыш (1), а с вероятностью (1-q) он желает получить выигрыш (2). Тогда ожидаемый выигрыш игрока 1 составит:
|
|
|
(7*p + 2*(1-p))*q + (6*p + 7*(1-p))*(1-q) = 6*pq – 5*q – p +7 (3)
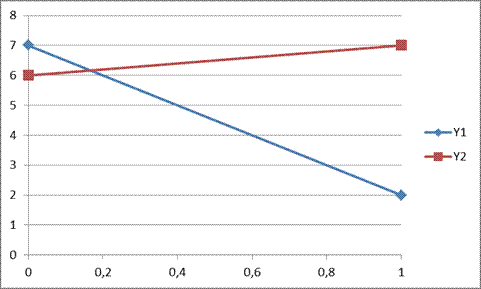
Рисунок 1
Сначала нужно найти максимин выражения (3), т. е. максимальное значение минимального выигрыша игрока 1, которое он соответствующим выбором р может себе обеспечить.
(3): (6*p – 5)*q – p + 7 (4)
Если р ≥ 5/6, то коэффициент в выражении (4) при q неотрицателен, и, следовательно, игрок 2 для уменьшения выигрыша своего противника может взять наименьшее значение q, т. е. 0. Тогда выигрыш 1 будет равен 7 – p. Тогда для максимизации этого выражения игроку 1 будет выгодно взять наибольшее р, следовательно его выигрыш окажется равным 7 – 5/6 = 37/6.
Если р < 5/6, то коэффициент в выражении (4) при q отрицателен, и, следовательно и игроку 2 будет выгодно взять значение q = 1. Тогда выигрыш 1 будет равен 5*p + 2. Следовательно его выигрыш окажется равным 25/6 + 2 = 37 /6.
Далее следует найти минимакс.
(3): (6*q – 1)*p – 5*q + 7
(5)
В случае, если q ≥ 1/6, то p = 0. Выигрыш 1 будет равен 7 – 5*q. Для минимизации стоит брать наименьшее значение q, тогда выигрыш составит 37/6. Если q < 1/6, то p = 1. Выигрыш будет равен q + 6. Тогда выигрыш составит 37/6.
Следовательно, смешанные стратегии игрока 1 (5/6, 1/6) и игрока 2 (1/6, 5/6) являются оптимальными стратегиями и представляют собой ситуацию равновесия. Число 37/6 является значением игры.
Многошаговые игры
Игра с выжиданием
Предположим, что в момент принятия решения о предоставлении двух услуг установке камер первого типа (1) и камер второго типа (2), фирмы могут использовать помимо стратегий К1, К2, КС1, КС2 стратегию выжидания. Она позволит фирмам А и В принимать решение только после действия конкурента. В таком случае игру с выжиданием можно иллюстрировать в виде «древовидного графа»
|
|
|
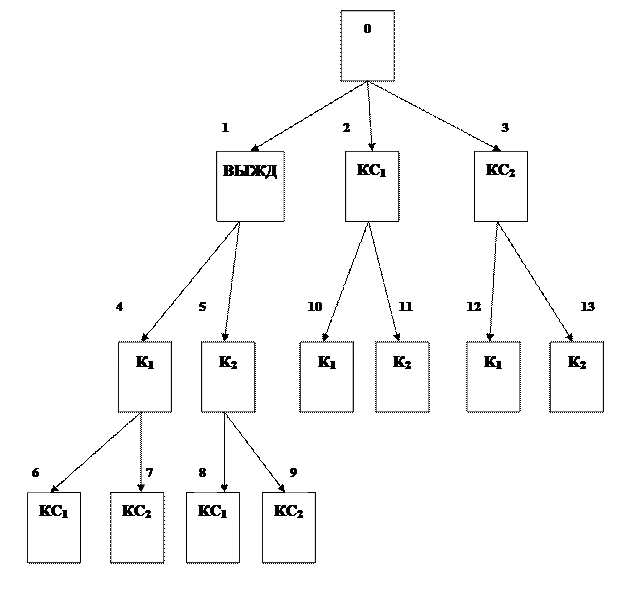
Рис. 3.1
В нашем примере «Сокол» имеет три информационных множества, состоящих из одной позиции каждая. Это значит, что «Сокол» действует все время в условиях полной информации об обстановке. В позиции 0 знает, что вообще еще ничего не произошло, а в позициях 4 и 5 знает, во-первых, об ожидании в течение некоторого времени, и, во-вторых, о том, какую продукцию выпускает «Чайка».
Напротив, «Чайка» имеет одно информационное множество, состоящее из трех позиций (1, 2 и 3-я). Это значит, что «Чайка» действует в условиях отсутствия информации, не зная в момент принятия решения, выжидает «Сокол» или нет, и если нет, то на какой продукции предприятие остановилось. Стратегией игрока является принятие в каждом информационном состоянии некоторого решения или, употребляя только что введенную терминологию, выбор в каждом информационном множестве некоторой альтернативы (очевидно, из всех позиций, принадлежащих одному информационному множеству, должны выходить одни и те же альтернативы). В этом смысле стратегию игрока следует понимать как функцию, заданную на семействе всех его информационных множеств, значением которой на каждом информационном множестве является некоторая альтернатива, принадлежащая этому информационному множеству.
Рассмотрим теперь информационные множества предприятия «Чайка». У предприятия «Чайка» одно информационное множество с двумя альтернативами, поэтому данное предприятие имеет лишь две стратегии: К1 и К2.
Предприятие «Сокол», напротив, имеет три информационных множества, и их альтернативы могут сочетаться друг с другом произвольным образом. Следовательно, «Сокол» имеет 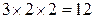 стратегий. Некоторые из них, впрочем, не представляют интереса. В связи с этим «реально возможных» стратегий у предприятия «Сокол», как это легко подсчитать, может быть лишь 6, и всего в игре может реализоваться
стратегий. Некоторые из них, впрочем, не представляют интереса. В связи с этим «реально возможных» стратегий у предприятия «Сокол», как это легко подсчитать, может быть лишь 6, и всего в игре может реализоваться  различных ситуаций.
различных ситуаций.
Каждая ситуация ведет к некоторой окончательной позиции. Так, принятие предприятием «Сокол» стратегии, состоящей в выборе им в позиции 0 альтернативы выжидания, а в каждой из позиций 4 и 5 альтернативы КС1, при принятии предприятием «Чайка» стратегии К1 приводит к окончательной позиции 6. Полное описание соответствия окончательных позиций Ситуациям игры можно свести в табл. 3.1.
|
|
|
Таблица 3.1
| «Сокол» «Чайка» | 0 – выжд 4 – КС1 5 – КС1 | 0 – выжд 4 – КС1 5 – КС2 | 0 – выжд 4 – КС2 5 – КС1 | 0 – выжд 4 – КС2 5 – КС2 | 0 – КС1 | 0 – КС2 |
| К1 | ||||||
| К2 | ||||||
| К1 | КС1 | К2 | КС2 | |
| К1 | х | 25% | 75% | 85% |
| КС1 | 75% | х | 50% | 60% |
| К2 | 25% | 50% | х | 10% |
| КС2 | 15% | 40% | 90% | х |
Подсчитаем выигрыши (игрока 1, т. е. предприятия «Чайка»), соответствующие окончательным позициям игры. Например, в позициях 6–9 «Чайка» сбывает, во-первых, 20 % своей продукции, а затем оставшиеся 80 % спроса покрываются совместно с предприятием «Сокол» согласно данным табл. 1.2. Таким образом, общий сбыт игрока 1 в позиции 6 будет составлять 20 % плюс 40 % от оставшихся 80 %, т. е. всего 52 %. Аналогичный подсчет выигрышей игрока 1 для остальных окончательных позиций сведен в табл.
Таблица 3.2
| № окончательной позиции | ||||||||
| Выигрыш «Чайки», в % |
 Подстановка в табл. 3.1 пяти значений выигрышей из табл. 3.2 в соответствующих окончательных позициях дает нам матрицу выигрышей
Подстановка в табл. 3.1 пяти значений выигрышей из табл. 3.2 в соответствующих окончательных позициях дает нам матрицу выигрышей
 40 40 80 80 25 85
40 40 80 80 25 85
60 28 60 28 50 10
Далее необходимо найти оптимальную стратегию предприятия «Сокол». В соответствии со смыслом принятого нами максиминного определения оптимальности она должна давать игроку 1 минимальный выигрыш, как бы тот ни играл (т. е. как бы тот ни старался этот выигрыш максимизировать). Это равносильно минимизации ожидаемого выигрыша игрока 1, если тот принимает свою оптимальную стратегию.
Всего выбираем 3 оптимальные стратегии:
40p+28 (1-p)
P=0 V=28
P=1 V=40
25p+50(1-P)
P=0 V=50
P=1 V=25
85p+10(1-P)
P=0 V=10
P=1 V=85
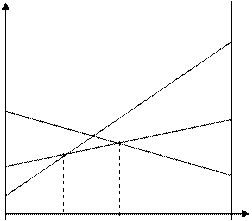 |
Минимакс этого последнего выражения равен 59 % и достигается при q = 37/22. Таким образом, предприятие «Сокол» должно выжидать с вероятностью, приблизительно равной 2/3, после чего действовать сообразно обстоятельствам.
|
|
|



