Главная | Обратная связь | Поможем написать вашу работу!

Р3. Движение тела при криволинейном движении.

4. Понятие силы и массы. Инерциальные системы отсчета. Законы Ньютона в механике.

· Си́ла — векторная физическая величина, являющаяся мерой воздействия на данное тело других тел, а также полей. Приложенная к массивному телу сила является причиной изменения его скорости или возникновения в нём деформаций и напряжений.

· Масса – это свойство тела, характеризующее его инертность. При одинаковом воздействии со стороны окружающих тел одно тело может быстро изменять свою скорость, а другое в тех же условиях – значительно медленнее. Принято говорить, что второе из этих двух тел обладает большей инертностью, или, другими словами, второе тело обладает большей массой.

· Инерциальная система отсчёта (ИСО) – система отсчёта, в которой справедлив первый закон Ньютона (закон инерции): все свободные тела (то есть такие, на которыене действуют внешние силы или действие этих сил компенсируется) движутся прямолинейно и равномерноили покоятся^[1]. Эквивалентной является следующая формулировка, удобная для использования в теоретической механике ^[2]:

· Инерциальной называется система отсчёта, по отношению к которой пространство является однородным иизотропным, а время — однородным.

1) Первый закон Ньютона: Существуют такие системы отсчета, называемые инерциальными, относительно которых свободные тела движется равномерно и прямолинейно.

· Первый закон механики, или закон инерции, как его часто называют, бал, по существу, установлен еще Галилеем, но общую формулировку ему дал Ньютон.

· Свободным телом – называют тело, на которое не действуют какие – либо другие тела или поля. При решении некоторых задач тело можно считать свободным, если внешние воздействия уравновешены.

· Системы отсчета, в которых свободная материальная точка покоится или движется прямолинейно и равномерно, называются инерциальными системами отсчета. Прямолинейное и равномерное движение свободной материальной точки в инерциальной системе отсчета называется движением по инерции. При таком движении вектор скорости материальной точки остается постоянным (= const). Покой точки является частным случаем движения по инерции (=0).

· В инерциальных системах отсчета покой или равномерное движение представляет собой естественное состояние, а динамика должна объяснить изменение этого состояния (т.е. появление ускорения тела под действием сил). Свободных тел, не подверженных воздействию со стороны других тел не существует. Однако, благодаря убыванию всех: известных взаимодействий с увеличением расстояния, такое тело можно реализовать с любой требуемой, точностью.

· Системы отсчета, в которых свободное тело не сохраняет скорость движения неизменной, называются неинерциальными. Неинерциальной является система отсчета, движущаяся с ускорением относительно любой инерциальной системы отсчета. В неинерциальной системе отсчета даже свободное тело может двигаться с ускорением.

· Равномерное и прямолинейное движение системы отсчета не влияет на ход механических явлений, протекающих в ней. Никакие механические опыты не позволяют отличить покой инерциальной системы отсчета от ее равномерного прямолинейного движения. Для любых механических явлений все инициальные системы отсчета оказываются равноправными. Эти утверждения выражают механический принцип относительности (принцип относительности Галилея). Принцип относительности является одним из наиболее общих законов природы, в специальной теории относительности он распространяется на электромагнитные и оптические явления.

· 3) Второй закон Ньютона

· Второй закон Ньютона описывает движение частицы, вызванное влиянием окружающих тел, и устанавливает связь между ускорением частицы, ее массой и силой, с которой на нее действуют эти тела:

· Если на частицу с массой т окружающие тела действуют с силой , то эта частица приобретает такое ускорение , что произведение ее массы на ускорение будет равно действующей силе.

· Математически второй закон Ньютона записывается в виде:

· На основе этого закона устанавливается единица силы — 1 Н (ньютон). 1 Н — это сила, с которой нужно действовать на тело массой 1 кг, чтобы сообщить ему ускорение 1 м/с².

· Если сила , с которой тела действуют на данную частицу, известна, то записанное для этой частицы уравнение второго закона Ньютона называют ее уравнением движения.

· Второй закон Ньютона часто называют основным законом динамики, так как именно в нем находит наиболее полное математическое выражение принцип причинности и именно он, наконец, позволяет решить основную задачу механики. Для этого нужно выяснить, какие из окружающих частицу тел оказывают на нее существенное действие, и, выразив каждое из этих действий в виде соответствующей силы, следует составить уравнение движения данной частицы. Из уравнения движения (при известной массе) находится ускорение частицы. Зная

· же ускорение можно определить ее скорость, а после скорости — и положение данной частицы в любой момент времени.

· Практика показывает, что решение основной задачи механики с помощью второго закона Ньютона всегда приводит к правильным результатам. Это и является экспериментальным подтверждением справедливости второго закона Ньютона.

· 4) Третий закон Ньютона.

· Третий закон Ньютона: Силы, с которыми тела действуют друг на друга, равны по модулям и направлены по одной прямой в противоположные стороны.

· Это означает, что если на тело А со стороны тела В действует сила , то одновременно на тело В со стороны тела А будет действовать сила , причем = -.

· Используя второй закон Ньютона, можно записать:

· ,

· Отсюда следует, что

· т. е. отношение модулей ускорений и взаимодействующих друг с другом тел определяется обратным отношением их масс и совершенно не зависит от характера действующих между ними сил. Более массивное тело получает меньшее ускорение, а легкое - большее.

· Важно понимать, что силы, о которых идет речь в третьем законе Ньютона, приложены к разным телам и поэтому они не могут уравновешивать друг друга.

5. Импульс. Закон сохранения импульса.

· Импульсом называют произведение массы тела на его скорость: . Импульс – векторная величина, направлен он всегда в ту сторону, в которую направлена скорость. Само слово «импульс» латинское и переводится на русский язык как «толкать», «двигать». Импульс обозначается маленькой буквой , а единицей измерения импульса является .

· теперь перейдем к следующему важному вопросу – закону сохранения импульса. Этот закон справедлив для замкнутой изолированной системы.

Определение: замкнутой изолированной системой называют такую, в которой тела взаимодействуют только друг с другом и не взаимодействуют с внешними телами.

Для замкнутой системы справедлив закон сохранения импульса: в замкнутой системе импульс всех тел остается величиной постоянной.

Обратимся к тому, как записывается закон сохранения импульса для системы из двух тел: .

Эту же формулу мы можем записать следующим образом: .

· Рис. 2. Суммарный импульс системы из двух шариков сохраняется после их столкновения

Обратите внимание: данный закон дает возможность, избегая рассмотрения действия сил, определять скорость и направление движения тел. Этот закон дает возможность говорить о таком важном явлении, как реактивное движение.

6. Работа постоянной и переменной силы. Мощность.

· A = |F|·|S|·cosa = (F·S)

· Работа постоянной силы равняется скалярному произведению силы на перемещение.

· Единица измерения работы - Джоуль. 1 Дж = 1 Н·м.

· Работа переменной силы

· Пусть тело движется прямолинейно с равномерной силой под углом £ к направлению перемещения и проходит расстояние S/ Работой силы F называется скалярная физическая величина, равная скалярному произведению вектора силы на вектора перемещения. A=F·s·cos £. А=0, если F=0, S=0, £=90º. Если сила непостоянная (изменяется), то для нахождения работы следует разбивать траекторию на отдельные участки. Разбиение можно производить до тех пор, пока движение не станет прямолинейным, а сила постоянной │dr│=ds.. Работа, совершенная силой на данном участке определяется по представленной формуле dA=F· dS· cos £= = │F│·│dr│· cos £=(F;dr)=Ft·dS A=F·S· cos £=Ft·S. Таким образом работа переменной силы на участке траектории равна сумме элементарных работ на отдельных малых участках пути A=SdA=SFt·dS= =S(F·dr).

· Мощность — физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.

· P=(A2-A1)/(t2-t1)-средняя мощность

· P=dA/dt -мгновенная мощность

7. Кинетическая энергия и ее связь с работой внешних сил. Потенциальные и не потенциальные поля. Потенциальная энергия: гравитационного поля; упругой пружины.Полная механическая энергия физической системы. Закон сохранения механической энергии.

· Потенциальное (или безвихревое) векторное поле в математике — векторное поле, которое можно представить как градиент некоторой скалярной функции координат. Необходимым условием потенциальности векторного поля в трёхмерном пространстве является равенство нулю ротора поля. Однако это условие не является достаточным - если рассматриваемая область пространства не является односвязной, то скалярный потенциал может быть многозначной функцией.

· Все силы, не являющиеся потенциальными, называются непотенциальными или диссипативными. К числу непотенциальных сил относятся, например, силы трения и сопротивления. Работа этих сил зависит от формы траектории между начальным и конечным положениями частицы (и не равна нулю при перемещении вдоль замкнутого контура).

· Гравитационная энергия — потенциальная энергия системы тел (частиц), обусловленная их взаимным гравитационным тяготением.

· Гравитационно-связанная система — система, в которой гравитационная энергия больше суммы всех остальных видов энергий (помимо энергии покоя).

· Общепринята шкала, согласно которой для любой системы тел, находящихся на конечных расстояниях, гравитационная энергия отрицательна, а для бесконечно удалённых, то есть для гравитационно не взаимодействующих тел, гравитационная энергия равна нулю. Полная энергия системы, равная сумме гравитационной и кинетической энергии, постоянна. Для изолированной системы гравитационная энергия является энергией связи. Системы с положительной полной энергией не могут быть стационарными.

· Найдём работу, совершаемую при деформации упругой пружины.
Сила упругости F _упр = – kx, где k – коэффициент упругости. Сила непостоянна, поэтому элементарная работа

dA = F d x = – kx d x.

· (Знак минус говорит о том, что работа совершена над пружиной). Тогда

(5.3.4)

· т.е. A = U ₁ – U ₂. Примем: U ₂ = 0, U = U ₁, тогда

(5.3.5)

На рис. 5.5 показана диаграмма потенциальной энергии пружины.

Рис. 5.5

· Здесь E = K + U – полная механическая энергия системы, К – кинетическая энергия в точке x ₁.

Закон сохранения энергии

Полная механическая энергия замкнутой системы тел остается неизменной

Закон сохранения энергии можно представить в виде

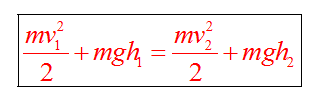
Если между телами действуют силы трения, то закон сохранения энергии видоизменяется. Изменение полной механической энергии равно работе сил трения

Рассмотрим свободное падение тела с некоторой высоты h1. Тело еще не движется (допустим, мы его держим), скорость равна нулю, кинетическая энергия равна нулю. Потенциальная энергия максимальная, так как сейчас тело находится выше всего от земли, чем в состоянии 2 или 3.

В состоянии 2 тело обладает кинетической энергией (так как уже развило скорость), но при этом потенциальная энергия уменьшилась, так как h2 меньше h1. Часть потенциальной энергии перешло в кинетическую.

Состояние 3 - это состояние перед самой остановкой. Тело как бы только-только дотронулось до земли, при этом скорость максимальная. Тело обладает максимальной кинетической энергией. Потенциальная энергия равна нулю (тело находится на земле).

Полные механические энергии равны между собой , если пренебрегать силой сопротивления воздуха. Например, максимальная потенциальная энергия в состоянии 1 равна максимальной кинетической энергии в состоянии 3.

А куда потом исчезает кинетическая энергия? Исчезает бесследно? Опыт показывает, что механическое движение никогда не исчезает бесследно и никогда оно не возникает само собой. Во время торможения тела произошло нагревание поверхностей. В результате действия сил трения кинетическая энергия не исчезла, а превратилась во внутреннюю энергию теплового движения молекул.

⇐ Предыдущая 123 4 5 Следующая ⇒

Воспользуйтесь поиском по сайту: