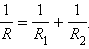При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.

Этот результат справедлив для любого числа последовательно соединенных проводников.

При параллельном соединении (рис. 1.9.2) напряжения U 1 и U 2 на обоих проводниках одинаковы: U 1 = U 2 = U.

Сумма токов I 1 + I 2, протекающих по обоим проводникам, равна току в неразветвленной цепи: I = I 1 + I 2.

Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δ t подтекает заряд I Δ t, а утекает от узла за то же время заряд I ₁Δ t + I ₂Δ t. Следовательно, I = I ₁ + I ₂.

Рисунок 1.9.2. Параллельное соединение проводников

Записывая на основании закона Ома

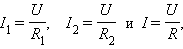
где R – электрическое сопротивление всей цепи, получим

 

19. Сторонние силы. ЭДС и напряжение.

 

Для того, чтобы поддерживать ток достаточно длительное время, необходимо от конца проводника с меньшим потенциалом непрерывно отводить, а к другому концу – с большим потенциалом – подводить электрические заряды. Т.е. необходим круговорот зарядов. Поэтому в замкнутой цепи, наряду с нормальным движением зарядов, должны быть участки, на которых движение (положительных) зарядов происходит в направлении возрастания потенциала, т.е. против сил электрического поля (рис. 7.3).

Рис. 7.3

Перемещение заряда на этих участках возможно лишь с помощью сил неэлектрического происхождения (сторонних сил): химические процессы, диффузия носителей заряда, вихревые электрические поля. Аналогия: насос, качающий воду в водонапорную башню, действует за счет негравитационных сил (электромотор).

Сторонние силы можно характеризовать работой, которую они совершают над перемещающимися по замкнутой цепи или ее участку зарядами.

Величина, равная работе сторонних сил по перемещению единичного положительного заряда в цепи, называется электродвижущей силой (ЭДС), действующей в цепи:

.

(7.4.1)

Как видно из (7.4.1), размерность ЭДС совпадает с размерностью потенциала, т.е. измеряется в вольтах.

Стороннюю силу, действующую на заряд, можно представить в виде:

(7.4.2)

– напряженность поля сторонних сил.

Работа сторонних сил на участке 1 – 2:

тогда

(7.4.3)

Для замкнутой цепи:

(7.4.4)

Циркуляция вектора напряженности сторонних сил равна ЭДС, действующей в замкнутой цепи (алгебраической сумме ЭДС) .

При этом необходимо помнить, что поле сторонних сил не является потенциальным, и к нему нельзя применять термин разность потенциалов или напряжение.

Напряжение - разность значения потенциала в начальной и в конечной точках траектории. A=qU => U=A/q =Дж/Кл=В
Разность потенциалов между 2-мя точками равно отношению работы электрического тока при перемещении заряда из начальной точки и конечную к этому заряду

 

20. Работа и мощность тока. Закон Джоуля-Ленца.

РАБОТА ПОСТОЯННОГО ТОКА
Работа тока - это работа электрического поля по переносу электрических зарядов вдоль проводника;

Работа тока на участке цепи равна произведению силы тока, напряжения и времени, в течение которого работа совершалась.

Применяя формулу закона Ома для участка цепи, можно записать несколько вариантов формулы для расчета работы тока:

По закону сохранения энергии:

работа равна изменению энергии участка цепи, поэтому выделяемая проводником энергия равна работе тока.

В системе СИ:

ЗАКОН ДЖОУЛЯ -ЛЕНЦА

При прохождениии тока по проводнику проводник нагревается, и происходит теплообмен с окружающей средой, т.е. проводник отдает теплоту окружающим его телам.

Количество теплоты, выделяемое проводником с током в окружающую среду, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока по проводнику.

По закону сохранения энергии количество теплоты, выделяемое проводником численно равно работе, которую совершает протекающий по проводнику ток за это же время.

В системе СИ:

[Q] = 1 Дж

 

МОЩНОСТЬ ПОСТОЯННОГО ТОКА

- отношение работы тока за время t к этому интервалу времени.

В системе СИ:

21. Закон Ома для неоднородного участка цепи, для замкнутой цепи.

Рассмотрим неоднородный участок цепи, на котором кроме электростатических сил, действуют сторонние силы. Для него:

.

(22.1)

и

,

(22.2)

тогда

.

(22.3)

Эта формула выражает закон Ома для неоднородного участка цепи в дифференциальной форме.

Рис. 22.1

 

Получим формулу закона Ома для неоднородного участка цепи в интегральной форме.

Рассмотрим неоднородный участок цепи (рис. 22.1).

Пусть электрический ток течёт вдоль тонких проводов. Тогда направление тока совпадает с направлением оси провода и плотность тока одинакова во всех точках сечения провода. Пусть площадь сечения провода S, а по длине провода S может быть неодинакова. Тогда

	.	(22.4)
	,	(22.5)

домножим (22.5) на и проинтегрируем по от точки 1 до точки 2

,

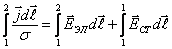(22.6)

заменив отношением (т.к. ), а в итоге получится:

.

(22.7)

Выражение представляет собой сопротивление участка контура длины 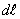, а интеграл от этого выражения – суммарное сопротивление R₁₂ участка цепи.

,

(22.8)

и – действующие на участке

,

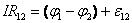(22.9)

где – полное сопротивление цепи.

.

(22.10)

Формула (22.10) выражает закон Ома в интегральной форме для неоднородного участка цепи.

Рис. 22.2

 

Положим получим выражение закона Ома для замкнутой цепи

.

(22.11)

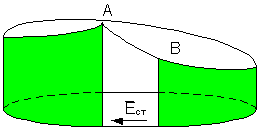
Как наглядно изобразить процесс, протекающий в замкнутой цепи постоянного тока?

Рис. 22.3

 

Точка А – соответствует положительной клемме источника, т. В – соответствует отрицательной клемме источника.

Процесс протекания тока можно представить так (рис. 22.3): положительные заряды – носители соскальзывают по наклонному желобу от точки А к точке В по внешнему участку цепи. Внутри источника от точки В к точке А их перемещают сторонние силы.

 

 

22. Магнитное поле. Вектор магнитной индукции и вектор напряженности магнитного поля. Принцип суперпозиции магнитных полей.

 

Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения ^[1], магнитная составляющая электромагнитного поле.

Магнитное поле может создаваться током заряженных частиц и/или магнитными моментамиэлектронов в атомах (и магнитными моментами других частиц, хотя в заметно меньшей степени) (постоянные магниты).

Магни́тная инду́кция — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой магнитное поле действует на заряд, движущийся со скоростью .

Напряженность магнитного поля первоначально была введена в форме закона Кулона через понятие магнитной массы, аналогичной электрическому заряду, как механическая сила взаимодействия двух точечных магнитных масс в однородной среде, которая пропорциональна произведению этих масс и обратно пропорциональна квадрату расстояния между ними: , где m ₁ и m ₂ - взаимодействующие магнитные массы; r - расстояние между точками, в которых магнитные массы считаются сосредоточенными; k - коэффициент, зависящий от свойств среды и системы единиц измерения.

Сила f направлена по прямой, соединяющей центры магнитных масс.

Магнитные массы одного знака отталкиваются, а противоположного - притягиваются.

Для количественной характеристики магнитного поля можно воспользоваться механической силой, действующей на положительный полюс пробного магнита, в той точке, где он расположен в пространстве. Напряженностью магнитного поля называется отношение механической силы, действующей на положительный полюс пробного магнита, к величине его магнитной массы или механическая сила, действующая на положительный полюс пробного магнита единичной массы в данной точке поля.

Напряженность изображается вектором H, имеющим направление вектора механической силы f.

.

(1)

Принцип суперпозиции магнитных полей: если магнитное поле создано несколькими проводниками с токами, то вектор магнитной индукции в какой-либо точке этого поля равен векторной сумме магнитных индукций, созданных в этой точке каждым током в отдельности:

Компьютерная программа позволяет изменять величину и направление токов, текущих по параллельным проводникам, расстояние между ними. Положение точки, в которой производится измерение вектора магнитной индукции результирующего поля, изменяется с помощью курсора мыши.

 

23. Закон Био-Савара-Лапласа и его применение для расчета магнитного поля прямолинейного проводника с током.

Магнитное поле создается вокруг электрических зарядов при их движении. Так как движение электрических зарядов представляет собой электрический ток, то вокруг всякого проводника с током всегда существует магнитное поле тока.

закона Био-Савара-Лапласа: каждый элемент проводника с током создает магнитное поле, вектор индукции которого в некоторой произвольной точке К определяется по формуле:

- закон Био-Савара-Лапласа.

Из закона Био-Совара-Лапласа следует, что направление вектора совпадает с направлением векторного произведения . Такое же направление дает и правило правого винта (буравчика).

Учитывая, что ,

- элемент проводника, сонаправленный с током;

- радиус-вектор, соединяющий c точкой K;

a - угол между и .

Закон Био-Савара-Лапласа имеет практическое значение, т.к. позволяет найти в заданной точке пространства индукцию магнитного поля тока, текущего по проводнику конечный размеров и произвольной формы.

Для тока произвольной формы подобный расчет представляет собой сложную математическую задачу. Однако, если распределение тока имеет определенную симметрию, то применение принципа суперпозиции совместно с законом Био-Савара-Лапласа дает возможность относительно просто рассчитать конкретные магнитные поля.

 

24. Применение закона Био-Савара-Лапласа для расчета магнитного поля на оси кругового тока.

Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:

. (1.5)

Расчет характеристик магнитного поля (и ) по приведенным формулам в общем случае сложен. Однако если распределение тока имеет определенную сим­метрию, то применение закона Био-Савара-Лапласа совместно с принципом суперпозиции позволяет просто рассчитать конкретные поля.

Магнитное поле в центре кругового проводника с током. Все элементы кругового проводника с током создают в центре магнитные поля одинакового направления – вдоль нормали от витка. Поэтому сложение век­торов можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору () и расстояние всех элементов проводника до центра кругового тока одинаково и равно, то согласно (1.4): .

Тогда . Следовательно, магнитная индукция поля в центре кругового проводника с током имеет вид: .

Опыт показывает, что магнитное поле действует не только на проводники с током, но и на отдельные заряды, движущиеся в магнитном поле. Сила, действующая на электрический заряд , движущийся в магнитном поле со скоростью , называется силой Лоренца и выражается формулой , (1.9) где – индукция магнитного поля, в котором заряд движется.

25. Взаимодействие 2-х параллельных проводников. Единица силы тока «Ампер».

Действием силы Ампера объясняется взаимодействие параллельных проводников с током (рис. 6.18).

Каждый из этих проводников имеет свое магнитное поле, действующее на соседний проводнике током. Так, проводник AA’, по которому проходит ток I₁, имеет магнитное поле, модуль индукции которого, как ука­зывалось раньше, равен B₁=μ₀I₁/ 2πr., где r - расстояние от проводника до точ­ки наблюдения.

 

Если проводник CC’ имеет длину Δl, находится на расстоянии r от проводника AA’ и по нему проходит ток I₂, то на него действует сила Ампера F̅₂₁ поскольку он находится в магнитном поле проводника AA’. Значение этой силы равно

F₂₁=B₁I₂Δl sin α.

Поскольку проводники параллельные и угол между проводником CC’ и вектором магнитной индукции равен 90°, то sin α = 1.

F =μ₀I₁I₂Δl / 2 πr.

Силу взаимодействия двух па­раллельных проводников с то­ком можно вычислить, зная лишь расстояние между ними и силы токов в них.

Как и при любом взаимодействии, для взаимодействующих параллельных провод­ников с током выполняется III закон дина­мики Ньютона: модули сил, действующих на проводники, одинаковые, а направления — противоположные.

Ампер (A) — единица измерения силы электрического тока в Международной системе единиц (СИ), одна из семи основных единиц СИ. В амперах измеряется также магнитодвижущая сила и разность магнитных потенциалов. Кроме того, ампер является единицей силы тока и относится к числу основных единиц в системе единиц МКСА (система единиц измерения электрических и магнитных величин).

Электрический ток силой один Ампер, проходящий в течение одной секунды, переносит один Кулон.

[ Сила электрического тока, А ] = [ Перенесенный заряд, К ] / [ Время переноса заряда, с ]

Электрический ток в 1 Ампер заряжает конденсатор в один Фарад за одну секунду на 1 Вольт.

[ Изменение напряжения на конденсаторе, К ] = [ Сила тока, А ] * [ Время протекания тока, с ] / [ Емкость конденсатора, Ф ]

Через проводник сопротивлением электрическому току 1 Ом под напряжением 1 Вольт протекает ток 1 Ампер. Это закон Ома.

[ Сила электрического тока, А ] = [ Напряжение, В ] / [ Сопротивление, Ом ]

Один Ватт тепловой мощности выделяется проводником при токе в 1 Ампер и напряжении на проводнике 1 Вольт.

[ Выделяемая тепловая мощность, Вт ] = [ Сила тока, А ] * [ Напряжение, В ]

[ Выделяемая тепловая мощность, Вт ] = [ Сила тока, А ] ^ 2 * [ Сопротивление проводника, Ом ]

26. Циркуляция вектора магнитной индукции. Закон полного тока в вакууме.

Аналогично циркуляции вектора напряженности электростатического поля введем циркуляцию вектора магнитной индукции. Циркуляцией вектора В по заданному замкнутому контуру называется интеграл где d l — вектор элементарной длины контура, направленной вдоль обхода контура, B_l=B cos a — составляющая вектора В в направлении касательной к контуру (с учетом выбранного направления обхода), a — угол между векторами В и d l.

Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора В): циркуляция вектора В по произвольному замкнутому контуру равна произведению магнитной постоянной m ₀ на алгебраическую сумму токов, охватываемых этим контуром:

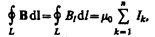(118.1) где n — число проводников с токами, охватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого образует с направлением обхода по контуру правовинтовую систему; ток противоположного направления считается отрицательным. Например, для системы токов, изображенных на рис. 173,

Выражение (118.1) справедливо только для поля в вакууме, поскольку, как будет показано ниже, для поля в веществе необходимо учитывать молекулярные токи.

Продемонстрируем справедливость теоремы о циркуляции вектора В на примере магнитного поля прямого тока I, перпендикулярного плоскости чертежа и направленного к нам (рис. 174). Представим себе замкнутый контур в виде окружности радиуса r. В каждой точке этого контура вектор В одинаков по модулю и направлен по касательной к окружности (она является и линией магнитной индукции). Следовательно, циркуляция вектора В равна

Согласно выражению (118.1), получим В× 2p r=m ₀ I (в вакууме), откуда

Таким образом, исходя из теоремы о циркуляции вектора В получили выражение для магнитной индукции поля прямого тока, выведенное выше (см. (110.5)).

Сравнивая выражения (83.3) и (118.1) для циркуляции векторов Е и В, видим, что между ними существует принципиальное различие. Циркуляция вектора Е электростатического поля всегда равна нулю, т. е. электростатическое поле является потенциальным. Циркуляция вектора В магнитного поля не равна нулю. Такое поле называется вихревым.

Теорема о циркуляции вектора В имеет в учении о магнитном поле такое же значение, как теорема Гаусса в электростатике, так как позволяет находить магнитную индукцию поля без применения закона Био - Савара – Лапласа.

27. Магнитное поле соленоида и тороида.

Найдем с помощью теоремы о циркуляции, индукцию магнитного поля внутри соленоида. Рассмотрим соленоид длиной l, который имеет N витков, и по которому течет ток (рис. 1). Будем считать длину соленоида во много раз больше, чем диаметр его витков. Экспериментальное изучение магнитного поля соленоида (см. главу "магнитное поле и его характеристики") показывает, что внутри соленоида поле однородно, вне соленоида — неоднородно и практически отсутствует.

На рис. 1 даны линии магнитной индукции внутри и вне соленоида. Чем соленоид длиннее, тем магнитная индукция вне его меньше. Поэтому приближенно можно полагать, что поле бесконечно длинного соленоида сосредоточено целиком внутри него, а поле соленоида можно не учитывать.

Для вычисления магнитной индукции В выберем замкнутый прямоугольный контур ABCDA, как показано на рис. 1. Циркуляция вектора В по замкнутому контуру ABCDA, который охватывает все N витков, используя формулу циркуляции вектора В, будет

Интеграл по ABCDA можно разложить на четыре интеграла: по АВ, ВС, CD и DA. На участках АВ и CD контур и линии магнитной индукции перпендикулярны: B _l =0. На участке вне соленоида B=0. На участке DA циркуляция вектора В равна В _l (контур и линии магнитной индукции совпадают); значит,

(1)

Из (1) приходим к формуле магнитной индукции поля внутри соленоида (в вакууме):

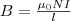(2)

Мы видим, что поле внутри соленоида однородно (при расчетах пренебрегают краевыми эффектами в областях, прилегающих к торцам соленоида). Но отметим, что вывод этой формулы не совсем корректен (поскольку линии магнитной индукции замкнуты, и интеграл по внешнему участку магнитного поля строго нулю не равен). Корректно найти поле внутри соленоида можно, используя закон Био — Савара — Лапласа; в результате получается такая же формула (2).

Важное практическое значение имеет также магнитное поле тороида — кольцевой катушки, у которой витки намотаны на сердечник, который имеет форму тора (рис. 2). Магнитное поле, как известно из опыта, сосредоточено внутри тороида, а вне его поле равно нулю.

В данном случае линии магнитной индукции, как следует из соображений симметрии, есть окружности, у которых центры расположены по оси тороида. В качестве контура возьмем одну такую окружность радиуса r. Тогда, используя теорему о циркуляции, B•2πr=μ₀NI, откуда следует, что магнитная индукция внутри тороида (в вакууме)

где N — число витков тороида.

Если контур проходит вне тороида, то токов он не охватывает и B•2πr = 0. Следовательно, что поле вне тороида отсутствует (что показывает и опыт).

 

28. Действие магнитного поля на проводник с током. Сила Ампера. Работа, совершаемая магнитным полем.

Магнитное поле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения; магнитная составляющая электромагнитного поля.

Магнитное поле действует с некоторой силой на любой проводник с током, находящийся в нем.

Если проводник, по которому протекает электрический ток подвесить в магнитном поле, например, между полюсами магнита, то магнитное поле будет действовать на проводник с некоторой силой и отклонять его.

Направление движения проводника зависит от направления тока в проводнике и от расположения полюсов магнита. Если поместить проволочную рамку, по которой протекает электрический ток, в магнитное поле, то в результате действия силы магнитного поля, рамка будет поворачиваться.

 

Действие магнитного поля на проводник с током Сила, действующая на проводник с током в магнитном поле, называется силой Ампера.
Сила действия однородного маг­нитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником: F=B.I.ℓ. sin α — закон Ампера.
Направление силы Ампера (правило левой руки) Если левую руку расположить так, чтобы перпендикулярная составляющая вектора В входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90° большой палец покажет направление силы, действующей на проводник с током

 

 

29. Движение заряженных частиц в электромагнитном поле. Сила Лоренца. Расчет радиуса, периода и частоты вращения для движения заряженной частицы в магнитном поле. Движение по винтовой линии, шаг винтовой линии.

Применение электронных пучков в науке и технике: электронная и ионная оптика, электронный микроскоп. Ускорители заряженных частиц.

Введём понятие элементарной частицы как объекта, механическое состояние которого полностью описывается заданием трех координат и трех компонент скорости его движения как целого. Изучению взаимодействий элементарных частиц с э.м. полем предпошлем некоторые общие соображения, относящиеся к понятию “частицы” в релятивистской механике.

Взаимодействие частиц друг с другом описывается (и описывалось до теории относительности) с помощью понятия силового поля. Каждая частица создает вокруг себя поле. На всякую другую частицу, находящуюся в этом поле, действует сила. Это касается как заряженных частиц, взаимодействующих с э.м. полем, так и не имеющих заряда массивных частиц, находящихся в гравитационном поле.

В классической механике поле являлось лишь некоторым способом описания взаимодействия частиц как физического явления. Положение вещей существенным образом меняется в теории относительности из-за конечной скорости распространения поля. Силы, действующие в данный момент на частицу, определяются их расположением в предшествующее время. Изменение положения одной из частиц отражается на других частицах лишь спустя некоторый промежуток времени. Поле становится физической реальностью, через посредство которой осуществляется взаимодействие частиц. Мы не можем говорить о непосредственном взаимодействии частиц, находящихся на расстоянии друг от друга. Взаимодействие может происходить в каждый момент лишь между соседними точками пространства (близкодействие). Поэтому можно говорить о взаимодействии частицы с полем и о последующем взаимодействии поля с другой частицей.

В классической механике можно ввести понятие абсолютно твердого тела, которое ни при каких условиях не может быть деформировано. Однако в невозможности существования абсолютно твердого тела легко убедиться с помощью следующего рассуждения, основанного на теории относительности.

Пусть твердое тело внешним воздействием в какой-нибудь одной его точке приводится в движение. Если бы тело было абсолютно твердым, то все его точки должны были бы прийти в движение одновременно с той, которая подверглась воздействию. (В противном случае тело должно было бы деформироваться). Теория относительности, однако, делает это невозможным, так как воздействие от данной точки передается к остальным с конечной скоростью, а потому все точки тела не могут одновременно начать двигаться. Поэтому под абсолютно твердым теломследует подразумевать тело, все размеры которого остаются неизменными в системе отсчета, где оно покоится.

Из сказанного выше вытекают определенные выводы, относящиеся к рассмотрению элементарных частиц. Очевидно, что в релятивистской механике частицам, которые мы рассматриваем как элементарные, нельзя приписывать конечных размеров. Другими словами, в пределах строгой специальной теории относительности элементарные частицы не должны иметь конечных размеров и, следовательно, должны рассматриваться как точечные.

Так как электрический ток представляет собой упорядоченное движение зарядов, то действие магнитного поля на проводник с током есть результат его действия на отдельные движущиеся заряды.

Силу, действующую со стороны магнитного поля на движущиеся в нем заряды, называют силой Лоренца.

Сила Лоренца определяется соотношением: F_л = q · V · B · sina

гдеq- величина движущегося заряда; V - модуль его скорости; B - модуль вектора индукции магнитного поля; a - угол между вектором скорости заряда и вектором магнитной индукции.

 

Обратите внимание, что сила Лоренца перпендикулярна скорости и поэтому она не совершает работы, не изменяет модуль скорости заряда и его кинетической энергии. Но направление скорости изменяется непрерывно.

Радиус окружности определяется: .

Период вращения частицы , то есть период вращения не зависит от скорости частицы и радиуса траектории.

Период вращения частицы, т. е. вре­мяТ, затрачиваемое ею на один полный оборот, T = 2nr/v. (т.е. период вращения частицы в однород­ном магнитном поле определяется только величиной, обратной удельному заряду).

30. Явление электромагнитной индукции. Правило Ленца. Закон Фарадея для электромагнитной индукции.

31. Явление самоиндукции. Индуктивность проводника. Энергия магнитного поля.

32. Понятие колебаний, типы колебаний. Механические свободные гармонические колебания (на примере пружинного маятника).

33. Идеальный электрический колебательный контур и собственные колебания в контуре.

34. Затухающие колебания в электрическом колебательном контуре.

35. Сложение колебаний: однонаправленные, взаимно перпендикулярные.

36. Понятие волны. Типы волн. Основные характеристики волн. Уравнение плоской бегущей волны. Фазовая скорость волны. Энергия волны. Вектор Умова.

37. Основные характеристики термодинамической системы (P, V, T). Уравнение Клайперона – Менделеева.

38. Температура. Шкала Кельвина и шкала Цельсия. Молекулярно-кинетический смысл абсолютной температуры.

39. Давление газа на стенку сосуда. Молекулярно-кинетический смысл давления.

40. Основные процессы в термодинамике: изохорный, изобарный, изотермический, адиабатический.

41. Внутренняя энергия идеального газа. Понятие теплоемкости. Теплоемкость газа при постоянном объёме и при постоянном давлении.

42. Работа, совершаемая идеальным газом. Первое начало термодинамики.

43. Тепловая машина. Цикл Карно. КПД цикла Карно.

44. Понятие энтропии термодинамической системы. Второе начало термодинамики.

45. Статистический смысл энтропии. Формула Больцмана.

46. Распределение Максвелла.

47. Наиболее вероятная, средняя и среднеквадратическая скорости молекул газа. Их зависимость от температуры газа и массы молекулы.

48. Распределение Больцмана. Барометрическая формула.

 

 

⇐ Предыдущая12345

Поделиться:

Воспользуйтесь поиском по сайту: