 |
При любых физических взаимодействиях энергия не возникает и не исчезает, а только превращается из одной формы в другую.
|
|
|
|
·
8. Электрический заряд. Закон сохранения электрического заряда. Закон Кулона. Напряженность электрического поля. Принцип суперпозиции. Силовые линии электростатического поля. Напряженность поля точечного заряда.
· Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.
Электрический заряд обычно обозначается буквами q или Q.
· В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной:
|
· Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака.
· Силы взаимодействия неподвижных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:
|
· Силы взаимодействия подчиняются третьему закону Ньютона: 
Они являются силами отталкивания при одинаковых знаках зарядов и силами притяжения при разных знаках (рис. 1.1.3). Взаимодействие неподвижных электрических зарядов называют электростатическим или кулоновским взаимодействием. Раздел электродинамики, изучающий кулоновское взаимодействие, называют электростатикой.
· Закон Кулона справедлив для точечных заряженных тел. Практически закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними.
· Коэффициент пропорциональности k в законе Кулона зависит от выбора системы единиц. В Международной системе СИ за единицу заряда принят кулон (Кл).
· Кулон – это заряд, проходящий за 1 с через поперечное сечение проводника при силе тока 1 А. Единица силы тока (ампер) в СИ является наряду с единицами длины, времени и массы основной единицей измерения.
|
|
|
· Коэффициент k в системе СИ обычно записывают в виде:
|
· где 
– электрическая постоянная.
· Напряженностью электрического поля называют физическую величину, равную отношению силы, с которой поле действует на положительный пробный заряд, помещенный в данную точку пространства, к величине этого заряда:
|
· Напряженность электрического поля – векторная физическая величина. Направление вектора 
в каждой точке пространства совпадает с направлением силы, действующей на положительный пробный заряд.
· Одной из основных задач электростатики является оценка параметров поля при заданном, стационарном, распределении зарядов в пространстве. Один из способов решения подобных задач основан на принципе суперпозиции. Суть его в следующем.
· Если поле создается несколькими точечными зарядами, то на пробный заряд q действует со стороны заряда qk такая сила, как если бы других зарядов не было. Результирующая сила определится выражением:
|
· – это принцип суперпозиции или независимости действия сил.
· Т.к. 
, то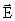 
– результирующая напряженность поля в точке, где расположен пробный заряд, так же подчиняется принципу суперпозиции:
| (1.4.1) |
· Это соотношение выражает принцип наложения или суперпозиции электрических полей и представляет важное свойство электрического поля. Напряженность результирующего поля, системы точечных зарядов равна векторной сумме напряженностей полей, созданных в данной точке каждым из них в отдельности.
· Для того чтобы описать электрическое поле, нужно задать вектор напряженности в каждой точке поля. Это можно сделать аналитически или графически. Для этого пользуются силовыми линиями – это линии, касательная к которым в любой точке поля совпадает с направлением вектора напряженности 
(рис. 2.1).
|
|
|
· 
Рис. 2.1
· Силовой линии приписывают определенное направление – от положительного заряда к отрицательному, или в бесконечность.
· Электрическое поле — пространство, обладающее свойством действовать с силой на электрический заряд, помещённый в это поле.
· Как показывает опыт, эта электрическая сила F пропорциональна величине пробного заряда q, находящегося в исследуемой точке поля.
· Поэтому отношение 
— уже не будет зависеть от величины пробного заряда. Оно определяется только свойством поля в данной точке. Это отношение принято в качестве силовой характеристики электрического поля и получило название напряженность.
· 
(1.2)
· Напряжённость данной точки электрического поля равна по величине и совпадает по направлению с силой, действующей на единичный положительный заряд, помещенный в эту точку (рис. 1.2.) В системе СИ напряжённость измеряется в ньютонах на кулон.
· 
·
· Рис. 1.2.
· Поле точечного заряда.
· Пусть поле создаётся точечным зарядом Q. Внесём в точку А этого поля пробный точечный заряд q (рис. 1.3.) На него в поле будет действовать сила, равная
· 
.
·
· Рис. 1.3.
· Но эту же силу можно записать, воспользовавшись законом Кулона (1.1)
· 
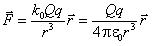
· Сопоставив эти два уравнения, легко получить выражение для напряжённости электрического поля, созданного точечным зарядом Q:
· 
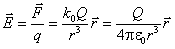(1.3)
· Напряжённость поля точечного заряда прямо пропорциональна величине заряда Q, создающего поле, и обратно пропорциональна квадрату расстояния от заряда, до той точки поля, в которой измеряется напряжённость.
· В любой точке такого поля вектор напряженности направлен по радиусу от положительного заряда (+ Q), либо к заряду, если он отрицателен (– Q).
· Электрические поля удобно представлять графически с помощью силовых линий.
·
9. Работа в электрическом поле. Потенциальная энергия. Потенциал электрического поля.
Рассчитайте работу по перемещению электрона между двумя точками в исследуемом поле. 
При перемещении пробного заряда q в электрическом поле электрические силы совершают работу. Эта работа при малом перемещении 
равна (рис. 1.4.1):
|
Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.
|
|
|
Потенциальная энергия заряда q, помещенного в любую точку (1) пространства, относительно фиксированной точки (0) равна работе A 10, которую совершит электростатическое поле при перемещении заряда q из точки (1) в точку (0):
|
· (В электростатике энергию принято обозначать буквой W, так как буквой E обозначают напряженность поля.)
· Так же, как и в механике, потенциальная энергия определена с точностью до постоянной величины, зависящей от выбора опорной точки (0). Такая неоднозначность в определении потенциальной энергии не приводит к каким-либо недоразумениям, так как физический смысл имеет не сама потенциальная энергия, а разность ее значений в двух точках пространства.
· Работа, совершаемая электростатическое полем при перемещении точечного заряда q из точки (1) в точку (2), равна разности значений потенциальной энергии в этих точках и не зависит от пути перемещения заряда и от выбора точки (0).
|
· Потенциальная энергия заряда q, помещенного в электростатическое поле, пропорциональна величине этого заряда.
· Физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:
|
· Потенциал φ является энергетической характеристикой электростатического поля.
· Работа A 12 по перемещению электрического заряда q из начальной точки (1) в конечную точку (2) равна произведению заряда на разность потенциалов (φ1 – φ2) начальной и конечной точек:
| A 12 = W p1 – W p2 = q φ1 – q φ2 = q (φ1 – φ2). |
· В Международной системе единиц (СИ) единицей потенциала является вольт (В).
| 1 В = 1 Дж / 1 Кл. |
· Во многих задачах электростатики при вычислении потенциалов за опорную точку (0) удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом:
|
|
|
· Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.
|
10. Потенциал электрического поля точечного заряда.Эквипотенциальные поверхности. Связь напряженности и потенциала.
Эквипотенциальные поверхности — поверхности, во всех точках которой потенциал имеет одно и то же значение.
11. Поток вектора напряженности электрического поля. Теорема Гаусса в вакууме.
Экспериментально установленные закон Кулона и принцип суперпозиции позволяют полностью описать электростатическое поле заданной системы зарядов в вакууме. Однако, свойства электростатического поля можно выразить в другой, более общей форме, не прибегая к представлению о кулоновском поле точечного заряда.
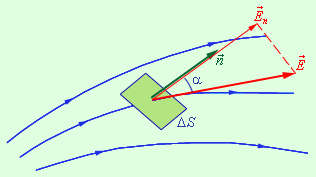
Введем новую физическую величину, характеризующую электрическое поле – поток Φ вектора напряженности электрического поля. Пусть в пространстве, где создано электрическое поле, расположена некоторая достаточно малая площадка Δ S. Произведение модуля вектора на площадь Δ S и на косинус угла α между вектором и нормалью 
к площадке называется элементарным потоком вектора напряженности через площадку Δ S (рис. 1.3.1):
| ΔΦ = E Δ S cos α = En Δ S, |
где En – модуль нормальной составляющей поля 
|
| Рисунок 1.3.1. К определению элементарного потока ΔΦ |
Рассмотрим теперь некоторую произвольную замкнутую поверхность S. Если разбить эту поверхность на малые площадки Δ Si, определить элементарные потоки ΔΦ i поля через эти малые площадки, а затем их просуммировать, то в результате мы получим поток Φ вектора через замкнутую поверхность S (рис. 1.3.2):
|
В случае замкнутой поверхности всегда выбирается внешняя нормаль.
|
| Рисунок 1.3.2. Вычисление потока Ф через произвольную замкнутую поверхность S |
Теорема Гаусса утверждает:
Поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε0.
|
Для доказательства рассмотрим сначала сферическую поверхность S, в центре которой находится точечный заряд q. Электрическое поле в любой точке сферы перпендикулярно к ее поверхности и равно по модулю
|
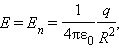
где R – радиус сферы. Поток Φ через сферическую поверхность будет равен произведению E на площадь сферы 4π R 2. Следовательно, 
Окружим теперь точечный заряд произвольной замкнутой поверхностью S и рассмотрим вспомогательную сферу радиуса R 0 (рис. 1.3.3).
|
|
|
|
| Рисунок 1.3.3. Поток электрического поля точечного заряда через произвольную поверхность S, окружающую заряд |
Рассмотрим конус с малым телесным углом ΔΩ при вершине. Этот конус выделит на сфере малую площадку Δ S 0, а на поверхности S – площадку Δ S. Элементарные потоки ΔΦ0 и ΔΦ через эти площадки одинаковы. Действительно,
| ΔΦ0 = E 0Δ S 0, ΔΦ = E Δ S cos α = E Δ S '. |
Здесь Δ S' = Δ S cos α – площадка, выделяемая конусом с телесным углом ΔΩ на поверхности сферы радиуса n.
Так как 
а 
следовательно 
Отсюда следует, что полный поток электрического поля точечного заряда через произвольную поверхность, охватывающую заряд, равен потоку Φ0 через поверхность вспомогательной сферы:
|
Аналогичным образом можно показать, что, если замкнутая поверхность S не охватывает точечного заряда q, то поток Φ = 0. Такой случай изображен на рис. 1.3.2. Все силовые линии электрического поля точечного заряда пронизывают замкнутую поверхность S насквозь. Внутри поверхности S зарядов нет, поэтому в этой области силовые линии не обрываются и не зарождаются.
Обобщение теоремы Гаусса на случай произвольного распределения зарядов вытекает из принципа суперпозиции. Поле любого распределения зарядов можно представить как векторную сумму электрических полей 
точечных зарядов. Поток Φ системы зарядов через произвольную замкнутую поверхность S будет складываться из потоков Φ i электрических полей отдельных зарядов. Если заряд qi оказался внутри поверхности S, то он дает вклад в поток, равный 
если же этот заряд оказался снаружи поверхности, то вклад его электрического поля в поток будет равен нулю.
Таким образом, теорема Гаусса доказана.
12. Применение теоремы Гаусса для расчета напряжённости электрического поля бесконечной плоскости.
Поверхностная плотность заряда на произвольной плоскости площадью S определяется по формуле: 
где d q – заряд, сосредоточенный на площади d S; d S – физически бесконечно малый участок поверхности.
Пусть σ во всех точках плоскости S одинакова. Заряд q – положительный. Напряженность во всех точках будет иметь направление, перпендикулярное плоскости S (рис. 2.11).
Очевидно, что в симметричных, относительно плоскости точках, напряженность будетодинакова по величине и противоположна по направлению.
Представим себе цилиндр с образующими, перпендикулярными плоскости, и основаниями Δ S, расположенными симметрично относительно плоскости (рис. 2.12).
| |||
| Рис. 2.11 | Рис. 2.12 | ||
Тогда 
Применим теорему Остроградского-Гаусса. Поток ФЕ через боковую часть поверхности цилиндра равен нулю, т.к. 
Дляоснования цилиндра 
Суммарный поток через замкнутую поверхность (цилиндр) будет равен: 
Внутри поверхности заключен заряд 
. Следовательно, из теоремы Остроградского–Гаусса получим: 
; откуда видно, что напряженность поля плоскости S равна:
| (2.5.1) |
Полученный результат не зависит от длины цилиндра. Это значит, что на любом расстоянии от плоскости 
13. Применение теоремы Гаусса для расчета напряжённости электрического поля бесконечной нити.
Пусть поле создается бесконечной цилиндрической поверхностью радиуса R, заряженной с постоянной линейной плотностью 
, где d q – заряд, сосредоточенный на отрезке цилиндра (рис. 2.14).
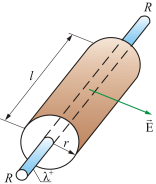
Рис. 2.14
Из соображения симметрии следует, что Е в любой точке будет направлена вдоль радиуса, перпендикулярно оси цилиндра.
Представим вокруг цилиндра (нити) коаксиальную замкнутую поверхность (цилиндр в цилиндре) радиуса r и длиной l (основания цилиндров перпендикулярно оси). Для оснований цилиндров 
для боковой поверхности 
т.е. зависит от расстояния r.
Следовательно, поток вектора через рассматриваемую поверхность, равен 
При 
на поверхности будет заряд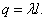 
По теореме Остроградского-Гаусса 
, отсюда
 .
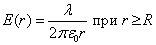| (2.5.6) |
Если 
, т.к. внутри замкнутой поверхности зарядов нет (рис.2.15).
Рис. 2.15
Если уменьшать радиус цилиндра R (при 
), то можно вблизи поверхности получить поле с очень большой напряженностью и, при 
, получить нить.
14. Применение теоремы Гаусса для расчета напряжённости электрического поля сферы.
Если то внутрь воображаемой сферы попадет весь заряд q, распределенный по сфере, тогда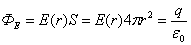 
,
откуда поле вне сферы:
| (2.5.7) |
Внутри сферы, при поле будет равно нулю, т.к. там нет зарядов: 
Рис. 2.17
Как видно из (2.5.7) вне сферы поле тождественно полю точечного заряда той же величины, помещенному в центр сферы.
15. Применение теоремы Гаусса для расчета напряжённости электрического поля шара.
Для поля вне шара радиусом R (рис. 2.18) получается тот же результат, что и для пустотелой сферы, т.е. справедлива формула: 
.
Но внутри шара при сферическая поверхность будет содержать в себе заряд, равный 
где ρ – объемная плотность заряда, равная: 
; 
– объем шара. Тогда по теореме Остроградского-Гаусса запишем:
,
т.е. внутри шара
 .
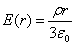| (2.5.8) |
Таким образом, внутри шара 
Рис. 2.18.
16. Электрическая ёмкость уединенного проводника. Конденсаторы. Расчет электроемкости для: плоского конденсатора. Параллельное и последовательное соединение конденсаторов.
Емкость уединенного проводника.
Уединенным будем называть проводник, размеры которого много меньше расстояний до окружающих тел. Пусть это будет шар радиусом r. Если потенциал на бесконечности принять за 0, то потенциал заряженного уединенного шара равен:  , где e - диэлектрическая проницаемость окружающей среды. Следовательно: 
эта величина не зависит ни от заряда, ни от потенциала и определяется только размерами шара (радиусом) и диэлектрической проницаемостью среды. Этот вывод справедлив для проводника любой формы.
| |
Электрической емкостью проводника наз. отношение заряда проводника к его потенциалу:  .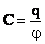
|
|
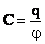
| Емкость определяется геометрической формой, размерами проводника и свойствами среды (от материала проводника не зависит). Чем больше емкость проводника, тем меньше меняется потенциал при изменении заряда. | Емкость шара в СИ:
 -
|
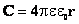| Единицы емкости. Емкостью 1Ф (фарад) обладает такой проводник, у которого потенциал возрастает на 1 В при сообщении ему заряда в 1 Кл. Емкостью 1Ф обладал бы уединенный шар, радиус которого был бы равен 13 радиусам Солнца. Емкость Земли 700 мкФ Если проводник не уединенный, то потенциалы складываются по правилу суперпозиции и емкость проводника меняется. | 
1 мкФ=10-6Ф
1нФ=10-9Ф
1пФ=10-12Ф
|
| Конденсаторы (condensare - сгущение) . Можно создать систему проводников, емкость которой не зависит от окружающих тел. Первые конденсаторы - лейденская банка (Мушенбрук, сер. XVII в.). | |
| Конденсатор представляет собой систему из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Проводники наз. обкладками конденсатора. Если заряды пластин конденсатора одинаковы по модулю и противоположны по знаку, то под зарядом конденсатора понимают абсолютное значение заряда одной из его обкладок. |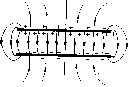 
|
| На рисунке - плоский и сферический конденсаторы. Поле плоского конденсатора почти все сосредоточено внутри (у идеального - все). Усферического - все поле сосредоточено между обкладками. | |
Электроемкостью конденсатора называют отношение заряда конденсатора к разности потенциалов между обкладками:  .
| 
|
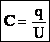
| При подключении конденсатора к батарее аккумуляторов происходит поляризация диэлектрика внутри конденсатора и на обкладках появляютсязаряды - конденсатор заряжается. Электрические поля окружающих тел почти не проникают через металлические обкладки и не влияют на разность потенциалов между ними. | |
Емкость плоского конденсатора.
 , т.о. емкость плоского конденсатора зависит только от его размеров, формы и диэлектрической проницаемости. Для создания конденсатора большой емкости необходимо увеличить площадь пластин и уменьшить толщину слоя диэлектрика.
|
|
|
|
