 |
Переход от одного опорного решения к другому
|
|
|
|
В транспортной задаче переход от одного опорного решения к другому осуществляется с помощью цикла. Для некоторой свободной клетки таблицы строится цикл, содержащий часть клеток, занятых опорным решением. По этому циклу перераспределяются объемы перевозок. Перевозка загружается в выбранную свободную клетку, и освобождается одна из занятых клеток, получается новое опорное решение.
Теорема 10 (о существовании и единственности цикла). Если таблица транспортной задачи содержит опорное решение, то для любой свободной клетки таблицы существует единственный цикл, содержащий эту клетку и часть клеток, занятых опорным решением.
Доказательство. Опорное решение занимает N=т+п— 1 клеток таблицы, которым соответствуют линейно независимые векторы-условия. Согласно теореме (о взаимосвязи линейной зависимости векторов-условий и возможности образования цикла) ни одна часть занятых клеток не образует цикл. Если же к занятым клеткам присоединить одну свободную, то соответствующие им т + п векторов линейно зависимы, и по той же теореме существует цикл, содержащий эту клетку. Предположим, что таких циклов два (i 1, j 1), (i 1, j 2), …, (iк, j 1) и (i 1, j 1), (i 2, j 1), …, (i 1, jl). Тогда, объединив клетки обоих циклов без свободной клетки (i 1 , j 1), получим последовательность клеток (i 1, j 2), …, (iк, j 1), (i 2, j 1), …, (i 1, jl), которые образуют цикл. Это противоречит линейной независимости векторов-условий, образующих базис опорного решения. Следовательно, такой цикл единственный.
Означенный цикл
Цикл называется означенным, если его угловые клетки пронумерованы по порядку и нечетным клеткам приписан знак «+», а четным — знак «-» (рисунок 10).

Рисунок 10
|
|
|
Сдвигом по циклу на величину θ называется увеличение объемов перевозок во всех нечетных клетках цикла, отмеченных знаком «+», на θ и уменьшение объемов перевозок во всех четных клетках, отмеченных знаком «—», на θ.
Теорема 11. Если таблица транспортной задачи содержит опорное решение, то при сдвиге по любому циклу, содержащему одну свободную клетку, на величину θ =  получится опорное решение.
получится опорное решение.
Доказательство. В таблице транспортной задачи, содержащей опорное решение, выберем свободную клетку и отметим ее знаком «+». По теореме (о существовании и единственности цикла) для этой клетки существует единственный цикл, который содержит часть клеток, занятых опорным решением. Пронумеруем клетки цикла, начиная с клетки, отмеченной знаком «+». Найдем θ =  и осуществим сдвиг по циклу на эту величину.
и осуществим сдвиг по циклу на эту величину.
В каждой строке и в каждом столбце таблицы, входящих в цикл, две и только две клетки, одна из которых отмечена знаком «+», а другая ― знаком «-». Поэтому в одной клетке объем перевозки увеличивается на θ, а в другой уменьшается на θ, при этом сумма всех перевозок в строке (или столбце) таблицы остается неизменной. Следовательно, после сдвига по циклу по-прежнему и запасы всех поставщиков вывозятся полностью, и запросы всех потребителей удовлетворяются полностью. Так как сдвиг по циклу осуществляется на величину θ =  , то все объемы перевозок будут неотрицательными. Следовательно, новое решение является допустимым.
, то все объемы перевозок будут неотрицательными. Следовательно, новое решение является допустимым.
Если оставить свободной одну из клеток с нулевым объемом перевозки, соответствующих  , то число занятых клеток будет равно N = т + п - 1. Одна клетка загружается (отмеченная знаком «+»), одна ― освобождается. Так как цикл единственный, то удаление из него одной клетки разрывает его. Цикл из оставшихся занятых клеток образовать нельзя, соответствующие векторы-условия линейно независимы, а решение является опорным.
, то число занятых клеток будет равно N = т + п - 1. Одна клетка загружается (отмеченная знаком «+»), одна ― освобождается. Так как цикл единственный, то удаление из него одной клетки разрывает его. Цикл из оставшихся занятых клеток образовать нельзя, соответствующие векторы-условия линейно независимы, а решение является опорным.
|
|
|

 Распределительный метод
Распределительный метод
Один из наиболее простых методов решения транспортных задач ― распределительный метод.
Пусть для транспортной задачи найдено начальное опорное решение Х 1и вычислено значение целевой функции на этом решении F (X 1). По теореме (о существовании и единственности решения) для каждой свободной клетки таблицы задачи можно построить единственный цикл, который содержит эту клетку и часть клеток, занятых опорным решением. Означив этот цикл и осуществив сдвиг (перераспределение груза) по циклу на величину θ =  , можно получить новое опорное решение Х 2.
, можно получить новое опорное решение Х 2.
Определим, как изменится целевая функция при переходе к новому опорному решению. При сдвиге на единицу груза по циклу, соответствующему клетке (l, k), приращение целевой функции Δ lk равно разности двух сумм:
Δ lk =  -
- 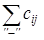 ,
,
где  — сумма стоимостей перевозок единиц груза в нечетных клетках цикла, отмеченных знаком «+»;
— сумма стоимостей перевозок единиц груза в нечетных клетках цикла, отмеченных знаком «+»;
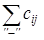 — сумма стоимостей перево
— сумма стоимостей перево  зок единиц груза в четных клетках цикла, отмеченных знаком «—».
зок единиц груза в четных клетках цикла, отмеченных знаком «—».
В клетках, отмеченных знаком «+», величины груза прибавляются, что приводит к увеличению значения целевой функции F (X), а в клетках, отмеченных знаком «—», величины груза уменьшаются, что приводит к уменьшению значения целевой функции.
Если разность сумм для свободной клетки (l, k)меньше нуля, т.е. Δ lk <0, то перераспределение величины θ по соответствующему циклу приведет к уменьшению значения F (X)на величину θ·Δ lk,т.е. опорное решение можно улучшить. Если же величины Δ lk, называемые оценками, для всех свободных клеток таблицы транспортной задачи неотрицательны, то значение целевой функции нельзя уменьшить и опорное решение оптимально. Следовательно, признаком оптимальности распределительного метода является условие Δ lk ≥0  хlk =0.
хlk =0.
Для решения транспортной задачи распределительным методом необходимо найти начальное опорное решение. Затем для очередной опорной клетки (l, k)построить цикл и вычислить оценку Δ lk. Если оценка неотрицательная, переходят к следующей свободной клетке. Если же оценка отрицательная, следует осуществить сдвиг по циклу на величину θ =  . В результате получится новое опорное решение.
. В результате получится новое опорное решение.
Для каждого нового опорного решения вычисление оценок начинается с первой свободной клетки таблицы. Очередность проверяемых свободных клеток целесообразно устанавливать в порядке возрастания стоимости перевозок cij,так как решается задача на нахождение минимума.
|
|
|
Пример 15. Решить распределительным методом транспортную задачу:
 bj
ai bj
ai
| |||
Решение. Строим начальное опорное решение:
 .
.
Затем вычисляем значение целевой функции на нем: F (X 1)=20·1+ +30·5+10·8 + 40·15 = 850.
 bj
ai bj
ai
| |||
Находим цикл для свободной клетки (1,2) таблицы, он включает клетки (1, 2), (1, 3), (3, 3), (3, 2). Вычисляем оценку Δ12 = (3+15)-(2+8)=8. Так как Δ12=8> 0, переходим к следующей свободной клетке (2, 1). Для нее цикл таков: (2, 1), (1, 1), (1, 3), (3, 3), (3, 2), (2, 2). Оценка Δ21=(4+2+8)-(1+15+5)=14-21=-7. Так как Δ21 = -7 < 0, определяем величину груза, перераспределяемого по циклу, θ =  {20, 40, 30} = 20. Приращение целевой функции Δ F = -7 · 20 = -140. Получаем новое опорное решение Х 2. Значение целевой функции на нем
{20, 40, 30} = 20. Приращение целевой функции Δ F = -7 · 20 = -140. Получаем новое опорное решение Х 2. Значение целевой функции на нем
F (X 2)= 20 · 2 + 20 · 4 + 10 · 5 + 30 · 8 + 20 · 15 = 710.
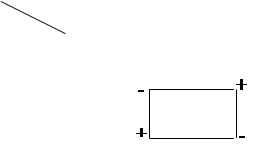 bj
ai bj
ai
| |||
Вычисляем Δ11 = (1 + 15 + 5) - (2 + 8 + 4) = 7 > 0, Δ12 = (3+15)-(2+8)=8> 0, Δ23 = (7 + 8) - (5 + 15) = -5 < 0, Δ31 = (6 + 5)—(4 + 8) = -1 < 0. Оценки можно вычислять до первой отрицательной. Так как Δ23 = -5 < 0, осуществляем сдвиг по циклу (2, 3), (3, 3), (3, 2), (2, 2) на величину θ =  {10, 20} = 10. Приращение целевой функции Δ F = -5 · 10 = -50. Получаем третье опорное решение Х 3. Значение целевой функции на нем
{10, 20} = 10. Приращение целевой функции Δ F = -5 · 10 = -50. Получаем третье опорное решение Х 3. Значение целевой функции на нем
F (X 3) = 20 · 2 + 20 · 4 + 10 · 7 + 40 · 8 + 10 · 15 = 660.
 bj
ai bj
ai
| |||
Вычисляем оценки для свободных клеток: Δ11= (1 + 7) — (2 + 4) = 2 > 0, Δ12 = (3 + 15) - (2 + 8) = 8 > 0, Δ22=(5+15)-(7+8)=5>0, Δ31=(6+7)—(4+15)=-6 < 0. Так как Δ31 = -6 < 0, осуществляем сдвиг по циклу (3, 1), (2, 1), (2, 3), (3, 3) на величину θ =  {20, 10} = 10. Приращение целевой функции Δ F = -6 · 10 = -60. Получаем четверки опорное решение Х 4. Значение целевой функции на нем
{20, 10} = 10. Приращение целевой функции Δ F = -6 · 10 = -60. Получаем четверки опорное решение Х 4. Значение целевой функции на нем
F (X 4) = 20 · 2 + 10 · 4 + 20 · 7 + 10 · 6 + 40 · 8 = 600.
 bj
ai bj
ai
| |||
Вычисляем оценки для свободных клеток Δ11 = (1 + 7) — (2 + 4) =2 > 0, Δ12 = (3 + 7 + 6) - (2 + 4 + 8) = 2 > 0, Δ22 = (5 + 6)-(4 + 8)=-1<0. Так как Δ22=-1< 0, осуществляем сдвиг по циклу (2,2), (3,2), (3,1), (2,1) на величину θ=  {10,40}=10. Приращение целевой функции Δ F = -1 · 10 = -10. Получаем пятое опорное решение Х 5.
{10,40}=10. Приращение целевой функции Δ F = -1 · 10 = -10. Получаем пятое опорное решение Х 5.
|
|
|
 bj
ai bj
ai
| |||
Значение целевой функции на нем
F (X 5)= 20 · 2 + 10 · 5 + 20 · 7 + 20 · 6 + 30 · 8 = 590.
Вычисляем оценки для свободных клеток: Δ11= (1 + 7) — (2 + 4) =2 > 0, Δ12 = (3 + 7) - (2 + 5) = 3 > 0, Δ33 = (15 + 5) - (7 + 8) = 5 > 0. Все оценки для свободных клеток положительные, следовательно, решение оптимально.
Ответ: min F (X) = 590 при  .
.
Метод потенциалов
Широко распространенным методом решения транспортных задач является метод потенциалов. Этот метод позволяет упростить наиболее трудоемкую часть вычислений — нахождение оценок свободных клеток.
Теорема 12 (признак оптимальности опорного решения). Если допустимое решение X = (хij), i = 1, 2,..., m, j = 1, 2,..., п транспортной задачи является оптимальным, то существуют потенциалы (числа) поставщиков иi, i = 1, 2,..,, т и потребителей v j, j = 1, 2,..., п, удовлетворяющие следующим условиям:
ui+ vj = cij при хij > 0 и ui+ vj ≤ cij при хij = 0.
Группа равенств ui+ vj = cij при хij > 0 используется как система уравнений для нахождения потенциалов. Нетрудно видеть, что эта система могла иметь несколько другой вид, например - ui+ vj = cij или ui- vj = cij,если перед тем, как записать двойственную задачу, все уравнения одной из групп уравнений исходной задачи умножить на (-1).
Данная система уравнений имеет т + п неизвестных иi, i =1,2,..., т и vj, j= 1, 2,..., п. Число уравнений системы, как и число отличных от нуля координат невырожденного опорного решения, равно т + п — 1. Так как число неизвестных системы на единицу больше числа уравнений, то одной из них можно задать значение произвольно, а остальные найти из системы.
Группа неравенств ui+ vj ≤ cij при хij = 0 используется для проверки оптимальности опорного решения. Эти неравенства удобно записать в виде
Δ ij = ui+ vj - cij ≤ 0 при хij = 0.
Числа Δ ij называются оценками свободных клеток таблицы или векторов ― условий транспортной задачи, не входящих в базис опорного решения. В этом случае признак оптимальности можно сформулировать так же, как в симплексном методе (для задачи на минимум): опорное решение является оптимальным, если для всех векторов-условий (клеток таблицы) оценки неположительные.
Оценки для свободных клеток транспортной таблицы используются для улучшения опорного решения. С этой целью находят клетку (l, k) таблицы, соответствующую max{Δ ij }= Δ lk. Если Δ lk ≤ 0, то решение оптимальное. Если же Δ lk > 0, то для соответствующей клетки (l, k) строят цикл и улучшают решение, перераспределяя груз θ =  по этому циклу.
по этому циклу.
|
|
|
|
|
|


