Математическая модель транспортной задачи

 

Переменными (неизвестными) транспортной задачи являются х_ij, i =1,2,..., m, j= 1, 2, ..., п — объемы перевозок от каждого i -го поставщика каждому j -му потребителю. Эти переменные можно записать виде матрицы перевозок:

.

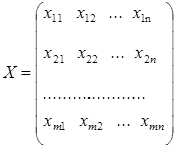Так как произведение с_ijх_ij определяет затраты на перевозку груза от i -го поставщика j -му потребителю, то суммарные затраты на перевозку всех грузов равны 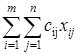. По условию задачи требуется обеспечить минимум суммарных затрат. Следовательно, целевая функция имеет вид:

F (X)= 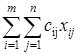→ min.

Система ограничений задачи состоит из двух групп уравнений. Первая группа из т уравнений описывает тот факт, что запасы всех т поставщиков вывозятся полностью:

, i =1, 2,..., т.

Вторая группа из п уравнений выражает требование полностью удовлетворить запросы всех п потребителей:

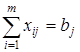, j = 1, 2,..., п.

Учитывая условие неотрицательности объемов перевозок, математическую модель задачи можно записать так:

F (X) = 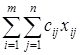→ min,

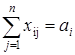, i =1, 2,..., т, 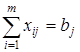, j =1, 2,..., п, х_ij ≥ 0, i =1,2,..., т, j =1,2,..., п.

В рассмотренной модели транспортной задачи предполагается, что суммарные запасы поставщиков равны суммарным запросам потребителей, т.е.

= .

Такая задача называется задачей с правильным балансом, а ее модель ― закрытой. Если же это равенство не выполняется, то задача называется задачей с неправильным балансом, а ее модель — открытой.

Математическая формулировка транспортной задачи такова: найти переменные задачи Х=(х_ij), i =1, 2,..., т, j = 1, 2,..., п,удовлетворяющие системе ограничений, условиям неотрицательности и обеспечивающие минимум целевой функции. Математическая модель транспортной задачи может быть записана и векторномвиде. Для этого рассмотрим матрицу А системы уравнений-ограничений задачи:

 

х ₁₁ х ₁₂ … х _{1 n} x ₂₁ x ₂₂… x _{2 n} … x_{m 1} x_{m 2}… x_mn

Сверху над каждым столбцом матрицы указана переменная задачи, коэффициентами при которой являются элементы соответствующего столбца в уравнениях системы ограничений. Каждый столбец матрицы А, соответствующий переменной х_ij, является вектором-условием задачи и обозначается через А_ij. Каждый вектор имеет всего т + п координат, и только две из них, отличные от нуля, равны единице. Первая единица вектора А_ij, стоит на i -м месте, а вторая на (т +j) - мместе, т.е.

Номер

координаты

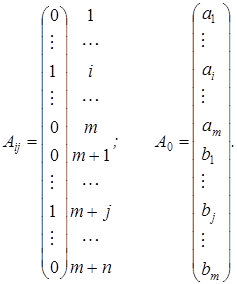
Обозначим через А ₀ вектор ограничений и представим систему ограничений задачи в векторном виде. Тогда математическая модель транспортной задачи запишется следующим образом:

F (X) = 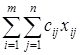→ min,

,

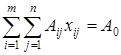х_ij ≥ 0, i =1,2,..., т, j =1,2,..., п.

Пример 12. Составить математическую модель транспортной задачи, исходные данные которой приведены в таблице:

bj ai

Решение. Введем переменные задачи (матрицу перевозок):

.

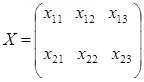Запишем матрицу стоимостей:

.

Целевая функция задачи равна сумме произведений всех соответствующих элементов матриц С и X:

F (X) = 3 х ₁₁+ 5 х ₁₂ + 7 х ₁₃ + 4 х ₂₁ + 6 х ₂₂ + 10 х ₂₃.

Данная функция, определяющая суммарные затраты на все перевозки, должна достигать минимального значения.

Составим систему ограничений задачи. Сумма всех перевозок, стоящих в первой строке матрицы X, должна равняться запасам 1-го поставщика, а сумма перевозок во второй строке матрицы X — запасам 2-го поставщика:

х ₁₁ + х ₁₂ + х ₁₃ = 40, х ₂₁ + х ₂₂ + х ₂₃ = 50.

Это означает, что запасы поставщиков вывозятся полностью. Суммы перевозок, стоящих в каждом столбце матрицы X, должны быть равны запросам соответствующих потребителей:

х ₁₁+ х ₂₁ = 20,

х ₁₂+ х ₂₂ = 30,

х ₁₃+ х ₂₃ = 40.

Это означает, что запросы потребителей удовлетворяются полностью. Необходимо также учитывать, что перевозки не могут быть отрицательными:

х_ij ≥ 0, i =1,2,..., т, j =1,2,..., п.

Следовательно, математическая модель рассматриваемой задачи такова: найти переменные задачи, обеспечивающие минимум функции

F (X) = 3 х ₁₁+ 5 х ₁₂ + 7 х ₁₃ + 4 х ₂₁ + 6 х ₂₂ + 10 х ₂₃

и удовлетворяющие системе ограничений

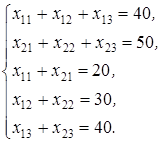
и условиям неотрицательности х_ij ≥ 0, i =1,2,..., т, j =1,2,..., п.

 

⇐ Предыдущая567891011121314Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: