Транспортная задача с ограничениями на пропускную способность

Пусть требуется при решении транспортной задачи ограничить перевозки от поставщика с номером l к потребителю с номером k. Возможны ограничения двух типов: 1) х_lk ≥ а; 2) х_lk ≤ b, где а и b — постоянные величины.

1. Если х_lk≥а, то необходимо прежде, чем решать задачу, сократить (уменьшить) запасы l -го поставщика и запросы k- гопотребителя на величину а (зарезервировать перевозку х_lk=а). После решения задачи в оптимальном решении следует увеличить объем перевозки х_lk на величину а.

2. Если х_lk ≤ b, то необходимо вместо k -гопотребителя с запросами b_k, ввести двух других потребителей. Один из них с номером k должен иметь запросы b'_k = b, а другой с номером п + 1 - запросы b_{n+ 1} = b_k- b. Стоимости перевозок для этих потребителей остаются прежними, за исключением стоимости с_{l ( n +1)}, которая принимается равной сколь угодно большому числу М (М>> 1). После получения оптимального решения величины грузов, перевозимых к (п +1)-му потребителю, прибавляются к величинам перевозок k-го потребителя. Так как с_{l ( n +1)}= М -самая большая стоимость перевозки, то в оптимальном решении клетка с номером (l,n +1) останется пустой, х_{l ( n +1)} = 0 и объем перевозки х_lk не превзойдет b.

Пример 17. Решить транспортную задачу, исходные данные которой приведены в таблице, при дополнительных условиях: объем перевозки груза от 1-го поставщика 2-му потребителю должен быть не менее 100 единиц (х ₁₂ ≥100), а от 3-го 1-му не более 200 единиц (х ₃₁ ≤ 200).

bj ai

Решение. Для того чтобы в оптимальном решении объем перевозки х ₁₂был не менее 100 единиц, при решении задачи будем предполагать, что запасы 1-го поставщика а ₁и запросы 2-го потребителя b ₂меньше фактических на 100 единиц. После получения оптимального решения объем перевозки х ₁₂увеличим на 100 единиц.

Для того чтобы удовлетворить требованию х ₃₁≤ 200, вместо 1-го потребителя введем двух других. Один из них под прежним первым номером имеет запросы b ₁ = 200 единиц и прежние стоимости перевозок единиц груза. Другому присвоим четвертый номер. Его запросы равны b ₄ = 500 — 200 = 300 единиц и стоимости перевозок единиц груза те же, что и у 1-го потребителя, за исключением с ₃₄, которую примем равной сколь угодно большому числу М, т.е. с ₃₄= М. После нахождения оптимального решения задачи объемы перевозок для 4-го потребителя необходимо прибавить к соответствующим объемам перевозок для 1-го потребителя.

В результате указанных преобразований таблица исходных данных задачи будет иметь вид, представленный в таблице:

bj ai
				М

Далее задачу решаем обычным методом потенциалов. Проверяем выполнение необходимого и достаточного условия существования решения задачи. Находим суммарные запасы поставщиков и запросы потребителей: а ₁ + а ₂ + а ₃ = 100 + 300 + 500 = 900;

b ₁ + b ₂ + b ₃ + b ₄ = 200 + 300 + 300 + 300 = 1100.

Задача с неправильным балансом. Вводим фиктивного поставщика с запасами а ₄= 1100 - 900 = 200.

Составляем начальное опорное решение Х ₁методом минимальной стоимости. Записываем матрицу стоимостей С:

Кружочками в матрице С отмечены минимальные элементы, а цифрами рядом со строками и столбцами ― порядок исключения из рассмотрения поставщиков и потребителей.

v ₁=1 v ₂=0 v ₃=1 v ₄=1

	bj ai
u 1=0			-	-
u 2=1			-	-
u 3=7					М   -
u 4=-1			-

Полученное решение X ₁имеет т + n — 1=4 + 4— 1 = 7 базисных переменных. Вычисляем значение целевой функции на этом опорном решении: F (X ₁) = 100·1+100·2+200·2+300·7+200·8+100·0+100·0=4400.

Для проверки оптимальности опорного решения находим потенциалы. Записываем систему уравнений для нахождения потенциалов и решаем ее:

Система состоит, из семи уравнений и имеет восемь переменных. Так как число неизвестных на единицу больше числа уравнений, то одному из потенциалов можно задать значение произвольно: пусть и ₁=0. Остальные потенциалы однозначно находятся из системы уравнений:

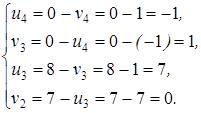
Значения потенциалов приведены в таблице. Находим оценки для свободных клеток таблицы: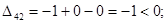

Опорное решение неоптимальное, так как имеется положительная оценка Δ₃₁ = 5 для клетки (3, 1). Отмечаем эту клетку знаком «+». Находим цикл для улучшения опорного решения. Определяем величину груза для перераспределения по циклу θ= {100, 200, 100} = 100. Осуществляем сдвиг по циклу на величину θ=100. Получаем второе опорное решение Х ₂.

v ₁=1 v ₂=5 v ₃=6 v ₄=1

	bj ai
u 1=0
u 2=1
u 3=2					М   -
u 4=-6		-	-

В таблице также записаны потенциалы и оценки для свободных клеток. Решение Х ₂оптимальное, так как все оценки неположительные. Запишем оптимальное решение исходной задачи. Для этого увеличим объем перевозки х ₁₂ на 100 единиц и объединим объемы перевозок 4-го потребителя, с объемами перевозок 1-го потребителя.

Получим Х ^*= .

Вычислим значение целевой функции на этом решении:

F (X*)=100·1+100·5+300·2+100·3+300·7+100·8=4400.

Ответ: min F (X) = 4400 при X* = .

В некоторых задачах требуется запретить перевозки от отдельных поставщиков отдельным потребителям. В таких случаях либо зачеркивают клетку таблицы транспортной задачи, либо назначают соответствующую этой клетке стоимость перевозки единицы груза сколь угодно большой, равной М >> 1. В остальном задача решается обычным способом. Для разрешимости данной задачи необходимо существование начального опорного решения.