 |
Определитель Вронского. Формула Лиувилля
|
|
|
|
Пусть имеется некоторая система из n векторных функций
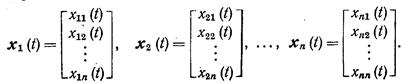
Тогда определителем Вронского, или вронскианом, называется определитель, составленный из компонент этих векторных функций. Таким образом, определитель Вронского имеет вид
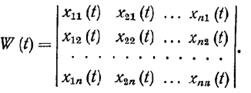
Если система векторных функций x1(t),..., хn(t) линейно-зависима, то определитель Вронского W(t)=0.
Пусть вектор-функции x1(t),..., xn(t) представляют собой n решений системы (3). Тогда, если определитель Вронского W(t) для этих решений обращается в ноль в какой-нибудь точке t0Î[а, b], то W(t) тождественно равен нулю на всем отрезке [а, b].
Пример: рассмотрим вектор-функции
Определитель Вронского для этих функций
При t = 0 W(0) = 0, но W(t) не равен тождественно 0. Отсюда следует, что данные вектор-функции х1(t) и x2(t) не могут быть решениями системы уравнений вида (3) с непрерывными коэффициентами, определенными на интервале, содержащем точку t=0.
Значение определителя Вронского в произвольной точке t можно вычислить с помощью рассмотренной ниже зависимости, называемой формулой Лиувилля.
Пусть x1(t), x2(t),..., xn(t) — n решений системы (3). Тогда между значениями определителя Вронского W(t) в точках t0 и t существует следующая зависимость:
– след матрицы A(t).
Линейная неоднородная система. Метод вариации произвольных постоянных
Рассмотрим линейную неоднородную систему (2)
Соответствующая ей однородная система (3)
Пусть x=y(t) и j(t) – два решения системы (2). Тогда разность
x(t)= y(t)–j(t)
Представляет собой решение однородной системы (3).
Общее решение системы (2) имеет вид
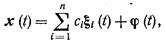
где ci – произвольные постоянные; xi(t) (i=1, 2, …, n) – фундаментальная система решений системы (3).
Частное решение системы (2) может быть найдено методом вариации произвольных постоянных. Рассмотрим этот метод. Пусть x1(t), x2(t), …, xn(t)— фундаментальная система решений системы (3). Частное решение неоднородной системы (2) будем искать в виде
|
|
|
полагая, что ci являются не постоянными, а некоторыми функциями t. Подставим это решение в систему (2):
Так как вектор-функции xi(t) – являются решениями однородной системы (3), то
поэтому
Это выражение представляет собой систему линейных алгебраических уравнений относительно сi(t) (i=l, 2,,..., n). Определитель этой системы уравнений есть определитель Вронского для фундаментальной системы решений. Он отличен от нуля, поэтому эта система имеет единственное решение сi’(t)=Фi(t) (i=l, 2,..., n).
Интегрируем полученные равенства:
Следовательно, искомое частное решение имеет вид
Значит, общее решение неоднородной системы будет
Формула Коши
При помощи формулы Коши можно выразить решение линейной неоднородной системы дифференциальных уравнений через некоторую фундаментальную систему решений соответствующей однородной линейной системы.
Рассмотрим неоднородную линейную систему дифференциальных уравнений (2), записанную в векторном виде
Соответствующая ей однородная система (3)
Пусть x1, x2, …, xn – фундаментальная система решения системы уравнений (3). Образуем матрицу X1(t), столбцы которой являются этими решениями:
Определитель матрицы Х1(t) представляет собой определитель Вронского. Он отличен от нуля для всех tÎ[a, b]. Следовательно, существует обратная матрица X-11(t) при каждом tÎ[а, b]. Составим матрицу
X(t, t0) = X1(t)X1-1(t0)
Столбцы этой матрицы также образуют фундаментальную систему решений системы уравнений (3). Отметим, что X(t, t0)= 
Назовем матрицу X(t, t0) фундаментальной матрицей системы (3). Эта матрица удовлетворяет матричному уравнению
Решение x(t) системы уравнений (3), удовлетворяющее начальным условиям x(t0)=x0, можно записать в виде
|
|
|
Тогда можно показать, что следующая формула, называемая формулой Коши, позволяет найти решение x(t) неоднородной системы (2), удовлетворяющее начальным условиям x(t0)=x0, если известна фундаментальная матрица X(t, t0) однородной системы (3):
Следует отметить, что если матрица А постоянная, т. е. рассматриваемая система дифференциальных уравнений является системой линейных уравнений с постоянными коэффициентами
то решение этой системы x(t), удовлетворяющее начальным условиям x(t0)=x0, запишется в виде
где X (f) — матрица, столбцы которой состоят из фундаментальной системы решений однородной системы уравнений xt'=Ах, причем X (t0) = E.
|
|
|
