 |
Понятие пространства состояний
|
|
|
|
С точки зрения анализа и синтеза систем представляется целесообразным разделить все переменные, характеризующие систему, на три группы:
1) входные переменные или входные воздействия mi, представляющие сигналы, генерируемые системами, внешними по отношению к исследуемой, и влияющие на поведение системы;
2) выходные переменные или переменные, характеризующие реакцию системы yj, позволяющие описать некоторые аспекты поведения системы, представляющие интерес для исследователя;
3) переменные (координаты) состояния или промежуточные переменные xk, характеризующие динамическое поведение исследуемой системы.
Величины mi, yj и xk предполагаются функциями времени. Для удобства оперирования с многомерными величинами совокупность входных переменных представим в виде вектора входа, совокупность выходных переменных – в виде вектора выхода, и совокупность переменных состояния – в виде вектора состояния:
 .
.
Множество всех значений, которые может принять вектор входа m в момент t, образует пространство входа системы. Множество всех значений, которые может принять вектор выхода y в момент t, образует пространство выхода системы. Множество всех значений, которые может принять вектор состояния x в момент t, образует пространство состояний системы.
Описание непрерывных систем с помощью системы дифференциальных уравнений
В любой момент времени t состояние системы является функцией начального состояния x(t0) и вектора входа m(t0, t), то есть
x(t)=F[x(t0); m(t0; t)],
где F – однозначная функция своих аргументов. Вектор выхода в момент t является также функцией x(t0) и m(t0; t) и может быть записан как
y(t)=z[x(t0); m(t0; t)].
Эти два уравнения часто называют уравнениями состояния системы. Для систем, описываемых дифференциальными уравнениями, эти уравнения могут быть записаны в следующей общей форме:
|
|
|
x(t)=F[x(t); m(t)],
y(t)=z[x(t); m(t)].
Такое описание системы носит название «вход–состояние–выход».
Если система описывается линейными дифференциальными уравнениями, то уравнения состояния системы сводятся к следующим:
dx(t)/dt=A(t)x(t)+D(t)m(t);
y(t)=B(t)x(t)+G(t)m(t),
где A(t) – матрица коэффициентов; D(t) – матрица управления; B(t) – матрица выхода; G(t) – матрица обхода системы.
Решение этой системы будем искать в форме
x(t)=p(t–t0)C1(t), (7)
где p(t–t0)=exp A(t–t0) – матрица перехода процесса, а С1(t) – вектор, зависящий от времени, заменяющий вектор начального состояния x0 в уравнении движения при отсутствии внешних воздействий. Дифференцируя это выражение по t, получаем
dx(t)/dt=Ax(t)+p(t–t0)dC1(t)/dt.
Если формула (7) является решением однородного уравнения, то величины в правых частях однородного уравнения и полученной формулы должны быть одинаковы. Отсюда
Dm(t)=p(t–t0)dC1(t)/dt.
Решая это уравнение относительно С1(t), получаем

Учитывая это выражение и определение матрицы перехода уравнение (7) приведем к виду

При t=t0, p(t–t0)=I и С2=x(t0). Отсюда находим

Описание систем переменными состояния
Линейная стационарная система может быть описана совокупностью линейных дифференциальных уравнений первого порядка с постоянными коэффициентами, которую можно представить в следующей векторно-матричной форме:
dv(t)/dt=Av(t),
где A – матрица коэффициентов; v(t) – вектор-столбец, представляющий собой входные переменные mi и координаты xk системы
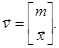
Если входные переменные рассматривать совместно с переменными состояния системы, то есть включить их в число координат системы, то вектор v можно считать вектором состояния системы увеличенной размерности.
|
|
|


