 |
Порядок выполнения работы и расчет ошибок измерений
|
|
|
|
1. Закрыть кассету с кристаллофосфором и, переводя переключатель в положение 1, измерить темновой ток фоторезистора.
2. Установить лампу накаливания на расстоянии R 1 напротив кристаллофосфора; включить лампу, переведя переключатель в положение 2; открыть кассету и освещать кристаллофосфор 3 мин (промежуток времени, за который возбуждение данного люминофора доходит до насыщения).
3. Закрыть кассету, выключить лампу накаливания и включить фоторезистор, переведя переключатель из положения 2 в положение 1. Отсчитав по секундомеру 10 секунд с момента закрытия кассеты, начать снимать показания микроамперметра. Общее время t измерений силы тока I 1– не менее 3 мин; результаты следует записать в соответствующий столбец таблицы 1.
Провести подобные измерения ещё четыре раза, сняв зависимости I 2(t), I 3(t), I 4(t) и I 5(t); полученные данные также занести в таблицу 1.
4. Повторить действия, описанные в пп. 2 и 3 при увеличении расстояния между кристаллофосфором и лампой до R 2. Данные измерений занести в таблицу, аналогичную таблице 1.
5. Если темновым током фоторезистора нельзя пренебречь, получить истинное значение фототока, вычтя из измеряемых показаний микроамперметра величину темнового тока (I ТЕМН).
6. Определить средние арифметические значения силы тока фоторезистора I СР в исследуемые моменты времени затухания люминесценции и полученные данные занести в таблицу (примем одинаковые обозначения силы тока через фоторезистор и интенсивности люминесценции, так как в данных условиях это прямопропорциональные величины).
7. По полученным данным построить график зависимости I от t для двух фиксированных расстояний R 1 и R 2.
|
|
|
Таблица 1
| t, с | I 1, мкА | I 2, мкА | I 3, мкА | I 4, мкА | I 5, мкА | I СР, мкА | y =  - 1
|
| R = … м; I ТЕМН = … мкА; I 0 = … мкА |
8. Построив два графика в координатах y = - 1 по оси ординат и t – по оси абсцисс (значения I 0, R 1 и R 2 заданы на стенде) и сравнив их с графиками функций, описываемых уравнениями (4) и (11), определите закон затухания люминесценции и сделайте вывод о том, какой вид люминесценции (внутрицентровая или рекомбинационная) наблюдался в эксперименте.
9. Для момента времени t 1 = 20 с, когда преобладают случайные ошибки измерений, по методу Стьюдента оценить, на какую величину истинное значение силы тока отличается от его среднего значения I СР. Для этого следует определить параметр Δ I, характеризующий ширину кривой распределения Стьюдента:
Δ I = a(n, P) S, (14)
где a(n, P) – коэффициент Стьюдента, который в случае пяти измерений и доверительной вероятности P = 0,95 равен 2,8. Множитель S, который входит в выражение (14), следует рассчитывать по формуле
S = 
. (15)
В конечном итоге результаты прямых измерений при t 1 = 20 c записать в виде
I ( P = 0,95) = I СР ± D I. (16)
10. Для момента времени t1 = 20 c (преобладают случайные ошибки) и t 2 = 100 c (преобладает приборная ошибка) рассчитать ошибки косвенных измерений величины y = - 1.
|
|
|
11. Провести линейный регрессионный анализ экспериментальной зависимости y = f (t). Задача линейного регрессионного анализа (метода наименьших квадратов) заключается в том, чтобы, зная положение некоторых точек на плоскости, полученных в результате эксперимента, провести линию регрессии так, чтобы сумма квадратов отклонений D i 2 вдоль оси y имеющихся точек от проведенной прямой была минимальной (принцип Лежандра).
Для уравнения прямой у = bt + a, где a и b – постоянные величины, задачу метода наименьших квадратов можно выразить так:
U = 
(17)
Построенная таким образом линия регрессии позволяет с некоторой вероятностью предсказать в интересующем нас интервале t любые значения y при отсутствующих в таблице значениях t. Для ее построения необходимо вычислить значения коэффициентов a и b, минимизирующих сумму отклонений U. Выражения для искомых коэффициентов можно найти, вычисляя частные производные функции U по коэффициентам a и b и приравнивая их нулю. Решая систему полученных уравнений, находим
a =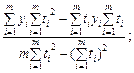 
b = 
. (18)
Таким образом, необходимо по формулам (18) рассчитать коэффициенты a и b и построить линию регрессии.
12. Построить экспериментальные данные в координатах lgI и t. Сделать вывод о механизме люминесценции.
Примечание: Пункты 10 – 12 рекомендуется выполнять в порядке УИРС.
Контрольные вопросы
1. Какие виды люминесценции различают в зависимости от вида возбуждения люминофора?
2. Чем отличается внутрицентровая люминесценция от рекомбинационной?
3. Что такое равновесные и неравновесные носители заряда?
4. Рассмотрите возможные типы генерации свободных носителей в люминофоре под действием света.
5. Вывести закон затухания внутрипримесной люминесценции.
6. С чем связано длительное послесвечение люминофора?
7. Каков механизм люминесценции исследуемого кристаллофосфора?
8. Что такое центры захвата?
9. Как зависит закон затухания люминесценции исследуемого люминофора от интенсивности возбуждающего света?
10. Дайте определение явлению люминесценции.
Список литературы
1. Физика твёрдого тела: Учебное пособие для технических университетов / И.К.Верещагин, С.М. Кокин, В.А. Никитенко, В.А. Селезнёв, Е.А. Серов; Под ред. И.К. Верещагина. – М.: Высшая школа, 2001. – 237 с.
|
|
|
2. Никитенко В.А., Кокин С.М. Физика. Часть III. Конспект лекций. – М.: МИИТ, 2007. – 196 с.
3. Селезнёв В.А., Тимофеев Ю.П. Методические указания к вводному занятию в лабораториях кафедры физики. – М.: МИИТ, 2006.
Работа 55к
ИССЛЕДОВАНИЕ ЛЮМИНЕСЦЕНЦИИ
КРИСТАЛЛОФОСФОРОВ
Цель работы. Изучение процессов генерации и рекомбинации неравновесных носителей заряда в твердых телах при возбуждении их светом, экспериментальная проверка кинетики затухания рекомбинационной люминесценции при наличии центров захвата (ловушек).
Введение
Для того, чтобы объяснить свойства люминесценции и отличить это явление от теплового равновесного излучения, приведем определение академика С. И. Вавилова: «...люминесценцией тела в данной спектральной области называется избыток излучения над температурным при условии, что это избыточное излучение обладает конечной длительностью, превышающей период световых колебаний».
В зависимости от вида возбуждения люминофора различают: фотолюминесценцию, возникающую в результате поглощения света; катодо-, рентгено- и радиолюминесценцию, возбуждаемую соответственно потоком быстрых электронов, рентгеновским излучением, a- и b-частицами, протонами, осколками ядерного деления; электролюминесценцию, возбуждаемую электрическим полем; хеми- и биолюминесценцию, при которых излучение света сопровождает химическую реакцию.
Люминофоры уже давно используются для приготовления светящихся составов, которыми покрываются различные опознавательные знаки; для изготовления ламп дневного света, экранов электроннолучевых приборов; применяются в телевизорах, осциллографах, электронных микроскопах и в рентгенотехнике. В последние годы, особенно в связи с разработкой полупроводниковых лазеров, область применения люминофоров существенно расширилась. Они стали применяться в вычислительной технике, системах передачи информации, а также в системах локации и автоматики на железнодорожном транспорте.
|
|
|
Теоретической основой современных представлений о механизме люминесценции кристаллофосфоров служит зонная теория твердых тел. В основе теории лежит энергетическая модель люминесцирующего кристалла. На рис. 1 схематически представлен энергетический спектр электрона в кристаллической решетке, имеющей какие-либо дефекты.
Состояния, принадлежащие зонам энергии (зона проводимости и валентная зона), связаны с основным веществом кристалла. Внедрение примесей в кристаллическую решетку основания люминофора либо присутствие в ней собственных дефектов вызывает появление локальных энергетических уровней внутри запрещенной зоны.
В зависимости от типа внутренних дефектов в кристаллофосфоре и от температуры среды можно рассмотреть различные процессы возбуждения (генерации) свободных носителей заряда. Например, тепловая генерация электронов из валентной зоны в зону проводимости (переход 1, что ведет к появлению свободных электронов в зоне проводимости и вакантных мест (дырок) в валентной зоне; ионизация примесных центров (переход 2), и т. д. Одновременно с генерацией возникает обратный процесс рекомбинации. Он заключается в том, что свободный электрон при встрече с дыркой занимает вакантное место (например, переход 3), либо наблюдается воссоединение свободного носителя с ионизированным примесным центром (переход 4).
При любой температуре между процессом тепловой генерации носителей и процессом их рекомбинации устанавливается равновесие, которому соответствует равновесная концентрация носителей. Такие носители называются равновесными.
Кроме теплового возбуждения возможны и другие способы генерации свободных носителей в кристаллах: под действием света, ионизирующих частиц и т. д., что также может привести к электронным переходам типа 1, 2, 5, 6, 7, 8(см. рис. 1). При световой генерации электронов из валентной зоны в зону проводимости через промежуточные состояния в запрещенной зоне в зависимости от энергетического положения этих состояний и температуры люминофора один из переходов может быть оптическим, а другой термическим (например, переходы 5, 7 – оптические; переходы 6, 8 – термические).
Появляющиеся дополнительно против равновесной концентрации свободные носители называются неравновесными. Созданные, например, при поглощении света неравновесные носители заряда первоначально могут иметь кинетическую энергию, значительно превышающую среднюю тепловую энергию равновесных частиц. Однако, в результате рассеяния на дефектах кристаллической решетки неравновесные носители заряда быстро (примерно за 10-10 с) передают ей свою избыточную энергию, поэтому распределение по энергиям неравновесных и равновесных носителей заряда будет на энергетической схеме одинаковым. Этот процесс сводится к тому, что неравновесные электроны, рассеивая свою избыточную энергию, как бы «опускаются» на дно зоны проводимости, а неравновесные дырки, рассеивая избыточную энергию, «поднимаются» к верхнему краю валентной зоны.
|
|
|
Свободные электроны непрерывно участвуют в процессе рекомбинации либо с ионизированным центром (переход 4, см. рис. 1), либо с дырками валентной зоны. Последний процесс может протекать или непосредственно через всю запрещенную зону (переход 3), или сначала электрон переходит на примесный уровень (переход 9), а затем с примесного уровня в валентную зону (переход 10). Могут наблюдаться случаи, когда первым имеет место электронный переход 10, а затем 9.
Выделение энергии может происходить или в виде кванта света, или в виде тепла (фононов). В первом случае рекомбинацию называют излучательной, во втором – безызлучательной.
Рассмотренная зонная модель люминофора (см. рис. 1) не учитывает колебательных движений атомов или ионов, поэтому с ее помощью нельзя показать безызлучательные переходы.
Излучательная рекомбинация рассмотренного выше типа называется рекомбинационной люминесценцией. Может возникнуть и другая ситуация. Если при введении примеси образуется центр, у которого имеется не только локальный уровень, занятый электроном (основной уровень), но и локальный возбужденный уровень, то поглощение возбуждающего света переведет электрон с основного уровня на возбужденный (переход 11), а возвращение электрона в нормальное положение будет сопровождаться излучением (переход 12). Такую люминесценцию называют внутрицентровой. Примеси, создающие центры свечения того или иного типа, называются активаторами. Обычно излучение в видимой области спектра происходит при переходах типа 9 или 12 (см. рис. 1).
В данной лабораторной работе используется люминофор, который в невозбужденном состоянии является почти изолятором, имеющим один тип центров свечения, на которых может происходить излучательная рекомбинация. При этом применяется световое возбуждение с энергией квантов, недостаточной для перехода электронов из зоны в зону (переход 1), поэтому следует ожидать возбуждение типа перехода 2 или 11.
Вследствие конечной длительности пребывания системы в возбужденном состоянии, люминесценция не исчезает мгновенно после прекращения возбуждения, а затухает с определенной скоростью. В случае внутрицентровой люминесценции излучательный переход в каждом центре происходит независимо от состояния других центров и определяется только его вероятностью.
Если N – число возбужденных центров свечения в момент времени t, а t – среднее время «жизни» возбужденного состояния, то число центров dN, переходящих в основное состояние за время dt, будет равно
dN = - N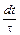 
. (1)
Преобразуя выражение (1) и интегрируя, получим
lnN = - 
+ const. (2)
Если в начале процесса (при t = 0) N = N 0, то
N = N 0 
. (3)
Интенсивность свечения I определяется числом излучательных переходов в единицу времени (для простоты будем считать её равной этому числу, хотя в целом это – энергетическая характеристика излучения):
I = - 
= 
= 
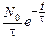. (4)
Таким образом, приходим к экспоненциальному закону затухания внутрицентровой люминесценции.
В случае рекомбинационной люминесценции интенсивность свечения пропорциональна скорости рекомбинации электронов с ионизированными центрами, а эта скорость определяется числом эффективных встреч между ними. Можно считать, что это число пропорционально произведению концентраций участников процесса – ионизированных центров свечения N A и свободных электронов п:
I = - 
= b N A n, (5)
где b – коэффициент рекомбинации.
Если концентрацией электронов в отсутствие возбуждения пренебречь, то N A = п и
I = - 
= b n 2. (6)
Разделяя переменные и интегрируя, найдем
= b t + const. (7)
Если при t = 0 имеем п = n 0, то
n =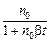 
. (8)
Подставляя последнее выражение в (6), получим
I = 
. (9)
При t = 0
I = I 0 = b n 02; n 0 = 
.
Окончательно получаем
I = 
. (10)
Закон затухания рекомбинационной люминесценции при сделанных предположениях выражается уравнением гиперболы второго порядка. Это уравнение для экспериментальной проверки удобно преобразовать, придав ему следующий вид:
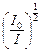- 1 = (I 0b)½ t, (11)
отсюда в координатах 
и t графиком функции должна получиться прямая линия.
Рассмотренные два основных типа люминесценции отличаются друг от друга также по зависимости затухания от интенсивности возбуждения. Как следует из выражений (4) и (11), при внутрицентровой люминесценции относительное изменение интенсивности свечения при затухании не зависит от I 0, а следовательно, и от интенсивности возбуждения, тогда как при рекомбинационной люминесценции это изменение тем быстрее, чем больше I 0. Поэтому слабое возбуждение люминесценции невыгодно в тех случаях, когда рекомбинационное послесвечение создает помехи, например, при наблюдении на экране движущихся предметов.
Из уравнения (10) следует, что при достаточно большом t интенсивность рекомбинационного послесвечения не зависит от начальной интенсивности. Кривые затухания, полученные после возбуждения люминофора излучениями различной интенсивности, будут асимптотически приближаться друг к другу.
Кроме центров свечения, в люминофоре могут находиться примесные центры, которые имеют свободный локальный уровень вблизи дна зоны проводимости. Эти центры могут захватывать электрон из зоны проводимости (см. рис. 1, переход 13) и удерживать его в течение длительного времени. Переход захваченного электрона в валентную зону для таких центров маловероятен, но существует вероятность обратного переброса электрона в зону проводимости (переход 14), где он в конечном итоге может принять участие в процессах рекомбинации. Такие центры, образующие метастабильные состояния в запрещенной зоне, называются электронными ловушками (центрами захвата). Возможно образование в кристалле и дырочных ловушек. Наличие таких ловушек обусловливает длительное затухание люминесценции кристаллов после прекращения их возбуждения. В этом случае для описания затухания люминесценции следует заменить вышеприведенные дифференциальные уравнения системой дифференциальных уравнений, содержащих несколько переменных, учитывающих захват электронов на ловушки.
Анализ этой системы показывает, что если ловушки расположены по соседству с центрами свечения и если возбужденные электроны пробегают очень малые расстояния (меньше 10-6 см), перемещаясь лишь от ловушки до центра свечения или наоборот, то такую систему можно рассматривать как независимую. В этом случае вероятность рекомбинации постоянна во времени, и затухание будет следовать экспоненциальному закону (в данной ситуации время t соответствует пребыванию электрона в ловушке).
Если ловушки распределены в пространстве независимо от центров свечения и пробег электрона достаточно велик, чтобы позволить ему рекомбинировать с большим числом центров (пробег больше 10-5 см), то вероятность рекомбинации будет пропорциональна числу ионизированных центров. Мы опять получаем для кинетики затухания уравнение гиперболы второго порядка. Скорость затухания при этом будет определяться, в основном, временем пребывания электронов на ловушках.
Таким образом, затухание по гиперболе второго порядка однозначно устанавливает, что люминесценция является рекомбинационной. Часто ситуация существенно усложняется из-за вклада в кинетику затухания ловушек различного типа, отличающихся друг от друга глубиной. Тем не менее, математический анализ процесса показывает, что и в этом случае затухание рекомбинационной люминесценции подчиняется гиперболическому закону, но с показателем степени 1 £ p £ 2.
Это приводит к уравнению гиперболы дробной степени
I = 
, (13)
впервые эмпирически полученному Э. Беккерелем.
Приборы и принадлежности: исследуемый порошковый люминофор (сульфид цинка с примесью меди: ZnS-Сu); источник засветки люминофора (светодиод с максимумом излучения на длине волны 410 нм); приемник излучения люминофора (фоторезистор); микроамперметр (используется комбинированный прибор ЭЛЕКТРОНИКА ММЦ-01 в режиме измерения тока с пределом до 2 мА); универсальный блок питания и сопряжения с персональным компьютером излучателя и приемника излучения (блок изготовлен в виде отдельного переносного устройства, включаемого в розетку с напряжением 220 В и частотой 50 Гц; на лицевой панели блока имеется надпись «УБПС-1»); секундомер; персональный компьютер (используется только при проведении измерений в автоматическом режиме).
|
|
|
