Порядок виконання роботи. Контрольні запитання. Питання для самоконтролю з теми “Магнетизм”. Модуль 4. 5. Коливання та хвилі.

Порядок виконання роботи.

1. Зібрати схему, зображену на рисунку 6.

2. Задати напругу і одержати на екрані осцилографа петлю гістерезису. Визначити х_в, у_в - координати вершин петлі ( в міліметрах) і внести в таблицю.

3. Повторити п. 2 при різних напругах.

4. Знаючи коефіцієнти підсилення вертикального ( g _у) и горизонтального ( g _х) підсилювачів осцилографа, розрахувати напруги   та .

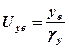5. З формул (4. 34) и (4. 37) одержати розрахункові формули для величин Н та В, за цими формулами розрахувати Н_в і В_в. Результати внести до таблиці та використати для побудови кривої намагнічування по вершинах петлі гістерезису.

6. Побудувати в протоколі максимальну петлю гістерезису, визначити х₀ і y₀ - координати точок перетину петлі гістерезису з осями координат, по одержаних розрахункових формулах (п. 5) обчислити коерцитивну силу та остаточну індукцію.

7. Визначити площу петлі гістерезису и обчислити теплові втрати за один цикл перемагнічування (4. 39) та втрати в 1 кг феромагнетика за одиницю часу (4. 40), враховуючи, що густина дорівнює 7800 кг/м³.

Таблиця для запису результатів вимірювання та обчислень

Хв, мм	Uхв, В	Нв, А/м	Yв, мм	Uyв, В	Вв, Тл

Контрольні запитання.

1. Як пов’язані між собою характеристики магнітного поля В та Н? Які їх одиниці вимірювання?

2. Намалюйте та поясніть хід кривої намагнічування.

3. Намалюйте та поясніть графік залежності В ( Н ) феромагнетика при циклічній зміні Н.

4. Намалюйте найпростішу електричну схему для спостереження петлі гістерезису на екрані осцилографа. Поясніть призначення елементів, які входять в схему.

5. Напишіть та поясніть формулу для розрахунку Н за напругою.

6. Доведіть, що напруга U_y пропорційна В феромагнетика.

7. Як визначити величини напруг U_x і U_y по відхиленню променя осцилографа?

8. Як визначити енергетичні втрати при перемагнічуванні?

9. В чому причина розігріву феромагнітного осердя при перемагнічуванні?

10. Навіщо осердя трансформатора роблять не суцільним, а складають з пластин?

Питання для самоконтролю з теми “Магнетизм”.

1. В чому полягає закон Біо- Савара- Лапласа? Як визначити напрям векторів В та Н у випадку прямого і колового струмів?

2. Дати визначення силових ліній магнітного поля. Накреслити картину силових ліній поля прямого і колового струму.

3. Чим відрізняються вихрові та потенціальні поля?

4. Як визначається сила, яка діє на провідник зі струмом в магнітному полі?

5. Яка сила діє на рухому заряджену частинку в магнітному полі?

6. Що називається потоком вектора магнітної індукції?

7. Що називається магнітним моментом контуру зі струмом?

8. Як орієнтований магнітний момент атома водню? Як орієнтований момент імпульсу його електрона?

9. Які явища свідчать про існування взаємодії, яка має назву магнітної?

10. Сформулюйте закон електромагнітної індукції Фарадея. Що означає знак мінус, який входить в аналітичний запис закону?

11. Яким способом можна збудити ЕРС індукції в замкненому контурі?

12. Чому дорівнює робота по переміщенню провідника зі струмом в магнітному полі?

13. Як обчислити роботу, яку виконує магнітне поле при обертанні контуру з струмом?

14. Яка сила виконує роботу при наближенні двох провідників, уздовж яких протікають паралельні струми?

Модуль 4

5. Коливання та хвилі.

5. 1. Власні коливання.

Коливаннями називаються процеси, коли деяка фізична величина періодично відхиляється в обидві сторони від сталого положення рівноваги під дією повертальної сили. Незважаючи на різноманітність коливань, усім їм властиві деякі характеристики:

1. Період коливань Т – час одного повного коливання.

2. Частота коливань n – число коливань, які виконуються за одиницю часу. Як видно з визначення, частота обернена періоду коливань: n = 1/Т.

3. Амплітуда коливань х ₀ – найбільше відхилення величини, що здійснює коливання, від положення рівноваги, яке приймається за нульове.

4. Закон коливань – залежність даної фізичної величини від часу: х ( t ).

Для виникнення та існування коливань необхідно, по – перше, систему вивести з положення рівноваги, по - друге, в цій системі повинна існувати сила, яка намагатиметься повернути систему до положення рівноваги. Якщо система після виведення з положення рівноваги залишається сама по собі, то коливання, що виникають, будуть називатись власними або вільними.

Повертальна сила підпорядковується узагальненому закону Гука:

F = -kx,                                                             (5. 1)

де зміщення від положення х завжди мале і напрямлене в сторону, протилежну напрямку дії повертальної сили (знак мінус). Коефіцієнт пропорціональності к, нарівні з мірою інертності – масою коливного тіла m, визначає власну циклічну частоту коливань w ₀ в нормалізованій формі запису рівняння Ньютона для системи, яка розглядається:

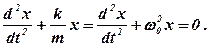                                   (5. 2)

Звідси витікає рівність:

                                                    (5. 3)

Очевидно, що допущення відсутності сил тертя і опору середовища (завжди реально існуючих) приводить до ідеалізованої моделі власних коливань. Їх відрізняючою рисою є сталість амплітуди х ₀ і, як наслідок, збереження механічної енергії коливань для будь-якого моменту часу:

                                     (5. 4)

Механічна енергія є сумою потенціальної і кінетичної складових, які взаємно пов’язані в процесі коливань таким чином, що їх сума Е ₀ лишається сталою (рис. 5. 1). Є математичний доказ того, що інтегральною формою або рішенням диференціального рівняння (5. 2) є гармонічні функції. Коливання, що відбуваються за законом синуса або косинуса, мають назву гармонічних. Рівняння гармонічних коливань мають вигляд:

                      (5. 5)

або

                      (5. 6)

де x – значення величини, що здійснює коливання, в момент часу t, x ₀ – амплітуда коливань. Величина (w₀ t + j₀ ), що знаходиться під знаком синуса або косинуса, має назву фази коливань, j₀ - початкова фаза коливань (дорівнює значенню фази в початковий момент часу). Величина w називається циклічною частотою коливань. Вона зв’язана з періодом рівністю:

                                                                   (5. 7)

За природою коливання можливо поділити на механічні та електромагнітні. Оскільки ми в подальшому будемо експериментально вивчати згасаючі електромагнітні коливання, то розглянемо більш детально саме їх.

Електромагнітні коливання виникають та відбуваються в коливальному контурі. Це замкнене коло, яке складається з послідовно з’єднаних конденсатора ємністю С, котушки індуктивністю L та резистора опором R (рис. 5. 2).

Замкнемо ключ на клему 1, зарядимо конденсатор. При цьому на верхній пластині конденсатора з¢ явиться позитивний заряд, на нижній – такий самий за величиною, але негативний заряд. Перекинемо тепер ключ на клему 2. Конденсатор почне розряджатись. Зростаючий струм розряду викличе в котушці електрорушійну силу (ЕРС) самоіндукції, напрямлену проти струму:

                             (5. 8)

Після того, як конденсатор розрядиться, струм почне зменшуватись. При цьому виникне ЕРС самоіндукції, напрямлена тепер за струмом. Внаслідок цього конденсатор спочатку перезарядиться, а потім почне розряджатись в зворотному напрямку. Для встановлення характеру коливань запишемо друге правило Кірхгофа для ділянки I 2 R L II. Напрям обходу контуру оберемо за рухом годинникової стрілки. При такому напрямку обходу струм розряду буде позитивний, а сила струму в котушці індуктивності буде дорівнювати швидкості, з якою зростає заряд нижньої пластини конденсатора С. В результаті одержимо:

                                                      (5. 9)

Розглянемо два частинні випадки.

а. Опором контуру R можна знехтувати. Покладемо в рівнянні (5. 9) R = 0 і врахуємо, що , де q – заряд нижньої пластини, 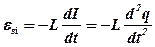 , одержимо

                                                     (5. 10)

Це рівняння не відрізняється від диференціального рівняння (5. 2), якщо провести заміну основної досліджуваної змінної x ( t ) на q(t) і визначити власну циклічну частоту LC контуру ( R @ 0), як:

                                                       (5. 11)

З цього рівняння виходить, що заряд на пластинах конденсатора змінюється за гармонічним законом, тобто

 ,                                            (5. 12)

а період визначається формулою Томсона

                                                 (5. 13)

Очевидно, що допущення відсутності електричного опору має наслідком умову збереження енергії електромагнітного поля для будь-якого моменту часу t, аналогічне умові (5. 4) для механічної енергії:

                                    (5. 14)

б. Опором контуру R нехтувати не можливо. Тоді, підставляючи в рівняння (5. 9) значення 

,

одержимо

.

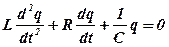Звідси, вводячи позначення

,                                                           (5. 15)

,                                                          (5. 16)

можна отримати

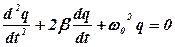                                            (5. 17)

Це рівняння повністю визначає характер коливань заряду і має назву рівняння згасаючих коливань в диференціальній формі. Розв’язання цього диференціального рівняння дає значення q ( t ), як функцію часу в явному вигляді. В курсі диференціальних рівнянь доводиться, що якщо виконується умова докритичних коливань b < w ₀, то розв’язання рівняння має вигляд:

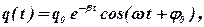                                        (5. 18)

де q ₀ та j₀ - довільні сталі, що визначаються з початкових умов,  - циклічна частота згасаючих коливань. Вираз (5. 18) має назву рівняння згасаючих коливань в інтегральній формі. Величина  має назву амплітуди згасаючих коливань. Графічна залежність q_m(t) побудована на рис. 5. 3. Пунктирна лінія – амплітуда згасаючих коливань.

Величина b має назву коефіцієнта згасання. Її фізичний зміст можна встановити, якщо розглянути проміжок часу t , за який амплітуда коливань зменшується в е разів (цей час має назву час релаксації). Можна довести, що коефіцієнт згасання обернений часу релаксації, тобто 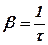 . Період згасаючих коливань тоді буде визначатись формулою

                                                     (5. 19)

Згасання за один період характеризують логарифмічним декрементом згасання q, який дорівнює натуральному логарифму відношення амплітуд через повний період коливань, тобто

                                   (5. 20)

Підставляючи вирази для амплітуд згасаючих коливань з урахуванням проміжку часу Т між амплітудами, можливо отримати

                                          (5. 21)

де N_e - число повних коливань, через які амплітуда коливань зменшиться в е разів. Таким чином, логарифмічний декремент згасання є величина, обернена числу коливань, через які амплітуда зменшується в е разів.

Якість коливальної системи характеризується також величиною її добротності. За визначенням добротність дорівнює

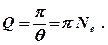                                                (5. 22)

Раніше відмічалося, що інтегральне розв’язання згасаючих коливань у вигляді (5. 18) є справедливим у випадку b < w ₀. Замінюючи коефіцієнт згасання та циклічну частоту відповідними виразами, можна одержати  , а отже 

                                                      (5. 23)

Таким чином, якщо умова (5. 23) не виконується, то коливання не виникають. Якщо система виведена з положення рівноваги, вона дуже швидко повертається в нього (демпфірує) при виконанні критичної умови: w₀ = b. В інших випадках, коли b > w ₀, система релаксує повільно (закритично).

⇐ Предыдущая16171819202122232425Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: