 |
Контрольні запитання.. 5.3. Звукові і світлові хвилі.
|
|
|
|
Контрольні запитання.
1. Які коливання мають назву вимушених?
2. Що таке ємнісний опір? Індуктивний опір?
3. Який зсув фаз між струмом та напругою у випадку ємнісного опору? У випадку індуктивного опору?
4. Як формулюється закон Ома для кола змінного струму?
5. Від чого залежить амплітуда та частота вимушених коливань?
6. Що таке резонанс? Які особливості резонансу у випадку послідовного та паралельного контуру (резонанс напруг та струмів)?
5. 3. Звукові і світлові хвилі.
При коливаннях положення рівноваги залишалось незмінним, інакше кажучи, коливання відбувались весь час в одній і тій самій обмеженій частині простору. Процес поширення коливань в просторі має назву хвильового процесу або просто хвилі.
Процес виникнення хвиль легше за все розглянути на прикладі поширення коливань у пружному середовищі. Будь-яка частинка цього середовища, що зрушується від положення рівноваги, діє на сусідні частинки, зміщує в свою чергу їх. Таким чином, коливання, які виникають в одній частині простору, поширюються все далі і далі – утворюється хвиля.
Згідно з природою розглядають хвилі механічні та електромагнітні. Хвиля має назву поздовжньої, якщо напрям коливання збігається з напрямом поширення хвилі, і поперечної, якщо коливання відбуваються перпендикулярно до цього напряму. Поперечні механічні хвилі поширюються або в твердому тілі, або на межі розділу рідина – газ. Поздовжні механічні хвилі можуть поширюватись в газі, рідині, твердому тілі. Електромагнітні хвилі завжди поперечні.
Геометричне місце точок, до яких поширились коливання у даний момент часу, має назву хвильового фронту. У будь – який момент часу хвильовий фронт у просторі існує тільки один. За формою фронту розглядають плоскі, циліндричні, сферичні хвилі. Найбільший інтерес викликає поширення у просторі гармонічних коливань, хвиля в цьому випадку також має назву гармонічної.
|
|
|
Розглянемо випадок гармонічної хвилі, що поширюється уздовж осі х, причому величина зміщення x залежить тільки від координати х, але не від координат y та z. Фронт хвилі в цьому випадку, очевидно, буде площиною, перпендикулярною до осі x. Саме тому, таку хвилю будемо називати плоскою гармонічною хвилею. Знайдемо рівняння такої хвилі, тобто вираз, який визначає зміщення частинки, що коливається в деякому середовищі, в точці з координатами ( x, y, z ) та в момент часу t. Нехай початкова фаза коливань частинок, розташованих у площині x = 0, дорівнює нулю, тобто зміщення цих частинок описується виразом 
. Будемо називати швидкість u зміщення точок, в яких фаза коливань приймає дане визначене значення, фазовою швидкістю хвилі. Таким чином, в момент часу t коливання в площині, що відповідає певному значенню x, будуть мати таку ж фазу, що й коливання, які відбувалися в площині x = 0 в момент часу 
, інакше кажучи,
(5. 38)
Одержаний нами вираз можна записати також у більш зручному вигляді, якщо ввести у розгляд поняття про довжину хвилі l. Це відстань, на яку поширюється хвиля за один період коливань. Згідно з визначенням, можна записати
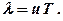(5. 39)
Оскільки період коливань можна записати через лінійну та циклічну частоту 
, то вираз для довжини хвилі може бути записаний у формі
або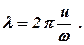 
(5. 40)
Таким чином, рівняння хвилі, що поширюється у напрямку осі x, приймає вигляд
(5. 41)
де величина 
має назву хвильового числа. Оскільки, як це виходить з останнього виразу, на відстані, що дорівнює довжині хвилі, зміна фази коливання складає 2p, то хвильове число дорівнює зміні фази хвилі на одиничній відстані у напрямку поширення хвилі. У випадку довільного напрямку поширення рівняння плоскої гармонічної хвилі може бути записано у вигляді
|
|
|
, (5. 42)
де 
- хвильовий вектор, який дорівнює за величиною хвильовому числу та спрямований уздовж напрямку поширення хвилі в даній точці.
|
|
|
