 |
5.2.2. Змінний струм, який тече крізь котушку індуктивності L (R ® 0, C ® ¥)
|
|
|
|
5. 2. 2. Змінний струм, який тече крізь котушку індуктивності L (R ® 0, C ® ¥ )
Тепер уявимо, що до котушки з індуктивністю L і нескінченно малим омічним опором R (рис. 5. 5. б) прикладається зовнішня напруга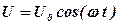 
. Згідно з другим правилом Кірхгофа можна записати 
, звідки для сили струму знайдемо інтегруванням
, (5. 26)
де амплітуда сили струму дорівнює
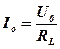. (5. 27)
Величина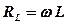 
має назву індуктивного опору.
Таким чином, в котушці протікає такий струм, який би утворився під дією зовнішньої напруги на індуктивному опорі. Фаза сили струму відстає на чверть періоду (p/2) від фази напруги.
5. 2. 3. Змінний струм, який тече крізь конденсатор ємністю С (R ® 0, L ® 0).
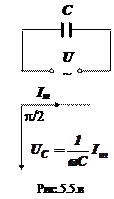Нехай тепер зовнішня напруга 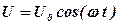прикладається до конденсатора ємністю С (рис. 5. 5. в). Тоді заряд на його обкладинках буде дорівнювати 
. Струм розряду - заряду конденсатора можна формально розглядати як струм, що протікає через конденсатор. Сила цього струму буде дорівнювати швидкості зміни заряду конденсатора:
, (5. 28)
де амплітуда сили струму дорівнює
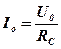. (5. 29)
Величина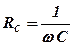 
має назву ємнісного опору.
5. 2. 4. Коло змінного струму, яке має послідовно з’єднані резистор, котушку індуктивності і конденсатор.
Розглянемо тепер випадок, коли джерело увімкнено в коливальний контур послідовно (Рис. 5. 6).
Будемо при цьому вважати, що внутрішнім опором джерела струму можна знехтувати та ЕРС діє за гармонічним законом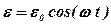 
. Спочатку, після ввімкнення джерела ЕРС, в контурі виникнуть власні коливання з частотою, яка визначається його параметрами L, C, R, та вимушені коливання з частотою джерела. Через деякий час власні коливання в контурі загасають. Таким чином, сила встановленого струму буде змінюватись за таким самим законом та з тією ж самою частотою, що й коливання джерела ЕРС, тобто 
. Треба визначити амплітуду коливань I0 та фазу запізнення j. Для цього визначимо напруги на окремих ділянках кола та знайдемо їх суму. Напруга на ділянці 1 – 2 (рис. 5. 6), де є активний опір, за фазою збігається з силою струму та дорівнює 
. Напруга на ділянці 2 – 3 з конденсатором відстає від сили струму на p/2 та дорівнює 
. Наприкінці, на ділянці 3 – 4, де ввімкнена котушка індуктивності, напруга випереджає силу струму на p/2 та може бути записана у вигляді 
|
|
|
Згідно з другим правилом Кірхгофа сума напруг уздовж замкненого кола дорівнює сумі ЕРС, які діють в цьому колі, тобто 
. Для знаходження амплітуди сили струму та фази запізнення звичайно використовують метод векторної діаграми. Це приводить до виразу для амплітуди сили струму:
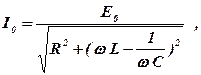(5. 30)
а зсув фаз між зовнішньою напругою та силою струму визначається формулою:
(5. 31)
Величина, що стоїть у знаменнику формули (5. 30), має назву повного опору кола або імпедансу:
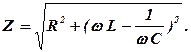(5. 32)
З рівнянь (5. 30) і (5. 31) виходить, що амплітуда сили струму та зсув його фази не залежать від початкових умов, а визначаються параметрами контуру L, C, R, а також амплітудою і частотою зовнішньої ЕРС.
Згідно з рівнянням (5. 30), амплітуда сили струму досягає максимального значення, коли повний опір контуру приймає мінімальне значення. Це відбудеться тоді, коли 
. При цій умові Z = R, а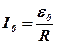 
. З попередньої умови знаходимо, що частота зовнішньої ЕРС в цей момент дорівнює власній частоті коливального контуру:
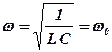. (5. 33)
|
|
|
Якщо активний опір R прямує до нуля, то амплітуда сили струму буде прямувати до нескінченності.
Явище різкого збільшення амплітуди сили струму в момент, коли збігаються частота зовнішньої ЕРС з власною частотою контуру, має назву резонансу. Явище резонансу в послідовному контурі має ще один дуже важливий аспект. Справа в тому, що в цей момент збігаються за величиною напруги на котушці та конденсаторі (фази їх протилежні) і тому зовнішня напруга буде дорівнювати напрузі на активному опорі. Це означає, що при цій частоті контур буде носити суто активний характер. Враховуючи ці аспекти, розглядуваний резонанс в послідовному контурі має назву резонансу напруг.
|
|
|
