 |
Лабораторна робота № 8.1 "Визначення відношення Сp/СV повітря методом Клемана – Дезорма".
|
|
|
|
Лабораторна робота № 8. 1 " Визначення відношення Сp/СV повітря методом Клемана – Дезорма".
Мета роботи: вивчення 1-го закону термодинаміки, ізопроцесів у газах, експериментальне визначення відношення теплоємностей повітря при сталому тиску і сталому об’ємі і порівняння його з теоретичним значенням.
8. 1. 1. Теплоємності і внутрішня енергія моделі ідеального газу.
Внутрішньою енергією тіла називають енергію, що залежить лише від його термодинамічного стану. Вона складається з кінетичної енергії хаотичного руху молекул, атомів, іонів і вільних електронів, потенційної енергії їхньої взаємодії, внутрішньоатомної і внутрішньоядерної енергії.
Перехід тіла з одного стану в інше називається термодинамічним процесом. Процес, що протікає при постійному значенні якого-небудь параметра функції стану, називається ізопроцесом: при Т = const - ізотермічним, при Р = const - ізобаричним, при V = const - і зохоричним, при S = const - ізоентропійним, наприклад, адіабатичним.
Термодинамічні процеси йдуть з передачею енергії від одного тіла до іншого чи від однієї частини тіла до іншої. Упорядкована передача енергії, що приводить до зміни форми чи об’єму першого тіла і до деформації або переміщення другого, представляє роботу, вона виміряється в джоулях (Дж).
Неупорядкована передача енергії при випадкових зіткненнях частинок на границі тіл чи усередині одного тіла, що не приводить до зміни форми чи об’єму, але супроводжується зміною інтенсивності руху частинок (температури), називається теплотою. У CI вона також виміряється в Дж. Робота А и теплота Q - це тільки міри переданої енергії, вони не є функціями стану тіла. Звичайно одночасно передається теплота і відбувається робота, але є виключення - адіабатичний (без теплообміну) і ізохоричний (без розширення і, отже, без здійснення роботи) процеси.
|
|
|
Щоб визначити теплоту, отриману тілом, використовують таку величину, як теплоємність тіла. Фізична величина, рівна кількості теплоти, необхідної для збільшення температури тіла на один кельвін, називається теплоємністю тіла:
(8. 10)
Теплоємність тіла виміряється в Дж/К. Відмінність в позначеннях δ (варіація) і d (диференціал) підкреслюють різницю між функцією процесу Q і параметром стану Т.
Для характеристики речовини, з якого складається тіло, використовують питому теплоємність чи молярну теплоємність сm .
Питомою теплоємністю називається фізична величина, яка дорівнює теплоємності тіла масою 1 кг і вимірювана в Дж/К· кг:
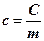
Молярна теплоємність - це фізична величина, яка дорівнює теплоємності тіла, що містить 1 моль речовини, вимірювана в Дж/К· моль:
Зв'язок між цими величинами:
Основне рівняння молекулярно-кінетичної теорії ідеального газу
(8. 11)
де n = N/V – концентрація частинок системи.
Воно зв'язує макроскопічний параметр стану - тиск р з концентрацією n і середньою енергією поступального руху молекули (потенціальна енергія в цій моделі дорівнює нулю).
З іншого боку, рівняння Клапейрона - Менделєєва можна записати у вигляді:
, (8. 12)
де k = R/NA = 1, 38´ 10-23 Дж/K - стала Больцмана.
Дорівнюючи праві частини рівнянь, одержуємо:
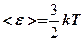(8. 13)
Виходячи з цього, Больцман припустив, що на кожен ступінь волі молекули не тільки ідеального, але і просто досить розрідженого газу припадає середня енергія, рівна kТ/2. Тоді в загальному випадку формула приймає вигляд:
|
|
|
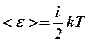(8. 14)
де i - число ступенів свободи молекули. При цьому i = 3 для одноатомних молекул (матеріальних точок), i = 5 для двохатомних молекул (гантелей, які мають 3 поступальні і 2 обертальні ступені свободи), i = 6 для трьох- і багатоатомних молекул (3 поступальні і 3 обертальні ступені свободи) відносно 3-х взаємно перпендикулярних осей обертання з моментами інерції, відмінними від нуля.
Помноживши праву частину рівняння на число молекул N, одержимо вираження для внутрішньої енергії всього ідеального газу:
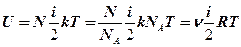(8. 15)
Це дозволяє розрахувати молярні теплоємності розрідженого газу при сталому об’ємі cmV і при сталому тиску cmp:
(8. 16)
(8. 17)
Відношення цих теплоємностей, яке називається коефіцієнтом Пуассона (показником адіабати)
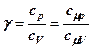> 1 (8. 18)
входить у рівняння Пуассона для адіабатичного процесу в розрідженому газі:
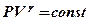(8. 19)
Адіабатичним процесом називається процес, що відбувається без теплообміну з іншими тілами. У випадку газу він полягає в його швидкому розширенні чи стиску, при якому енергія передається навколишнім тілам чи відбирається від них тільки у виді роботи, а теплопередача практично не встигає початися, чому сприяє і теплоізолююча оболонка судини.
|
|
|
