Главная | Обратная связь | Поможем написать вашу работу!

Представление информации в памяти компьютера

Представление символьной информации

для представления текстовой (символьной) информации в компьютере используется алфавит мощностью 256 символов. Один символ такого алфавита несет 8 бит информации, т.к. 2⁸ = 256. но 8 бит = 1 байту, следовательно, двоичный код каждого символа в компьютерном тексте занимает 1 байт памяти.

Пример 1 сколько бит памяти компьютера займет слово «Микропроцессор»?

Решение. Слово состоит из 14 букв. Каждая буква является символом компьютерного алфавита и поэтому занимает 1 байт памяти. Слово займет 14 байт = 112 бит памяти, т.к. 1 байт = 8 бит.

Варианты самостоятельной работы

1) Если досье на преступников занимают 45 мегабайт, и каждое из них имеет объем 12 страниц (48 строк по 64 символа в каждой), то число досье равно…?

2) Если вариант текста в среднем имеет объем 20 килобайт (на каждой странице текста 40 строк по 64 символа в каждой), то количество страниц в тексте равно…?

3) Сведения о сотруднике хранятся в виде строки из 2048 символов. Сведения обо всех 8192 сотрудниках можно разместить на минимальном числе дискет емкостью 1.2Мбайт, равном…?

4) Максимальное количество страниц книги (32 строки по 64 символа), которое поместится в файле объемом 640 Кбайт, равно…?

5) Объем текстовой информации в сообщении на 40 страницах (на странице 40 строк и 80 символов в строке) равен…?

6) Максимальное количество книг (каждая объемом 200 страниц, на каждой странице 60 строк, 80 символов в строке), полностью размещенных на лазерном диске емкостью 600 Мбайт, равно…?

7) сколько килобайтов составит сообщение, содержащее 12288 битов?

8) Вычислите объем текстовой информации в мегабайтах «Современного словаря иностранных слов» из 740 страниц, если на одной странице размещается в среднем 60 строк по 80 символов.

9) В текстовом режиме экран разбивается на 25 страниц по 80 символов в строке. Определите объем текстовой информации, занимающий весь экран монитора.

10) Подсчитайте объем информации в романе А. Дюма «Три мушкетера» и определите, сколько близких по объему произведений можно разместить на одном лазерном диске емкостью 600 Мбайт. В романе 500 страниц, на каждой странице 48 строк, в каждой строке 53 символа.

Представление числовой информации

для представления чисел в памяти компьютера используются два формата: формат с фиксированной точкой и формат с плавающей точкой. В формате с фиксированной точкой представляются только целые числа, в формате с плавающей точкой – вещественные числа (целые и дробные).

Целые числа

множество целых чисел, представляемых в памяти ЭВМ, ограничено. Диапазон значений зависит от размера ячеек памяти, используемых для их хранения. в k-разрядной ячейке может храниться 2^k различных значений целых чисел.

Пример 1 Пусть для представления целых чисел в компьютере используется 16-разрядная ячейка (2 байта). Определить, каков диапазон хранимых чисел, если а) используются только положительные числа;

б) используются как положительные, так и отрицательные числа в равном количестве.

Решение. Всего в 16-разрядной ячейке может храниться 2¹⁶ = 65536 различных значений. Следовательно:

а) диапазон значений от 0 до 65535 (от 0 до 2^k^-1);

б) диапазон значений от –32768 до 32767 (от -2^k^-1 до 2^k^-1-1).

Чтобы получить внутреннее представление целого положительного числа N, хранящегося в k-разрядном машинном слове, необходимо:

1) перевести число N в двоичную систему счисления;

2) полученный результат дополнить слева незначащими нулями до k разрядов.

Пример 2 получить внутреннее представление целого числа 1607 в 2-байтовой ячейке.

Решение. N = 1607₁₀ =11001000111₂. Внутреннее представление этого числа в ячейке будет следующим: 0000 0110 0100 0111. шестнадцатеричная форма внутреннего представления числа получается заменой 4-х двоичных цифр одной шестнадцатеричной цифрой: 0647.

Для записи внутреннего представления целого отрицательного числа (-N) необходимо:

1) получить внутреннее представление положительного числа N;

2) получить обратный код этого числа заменой 0 на 1 и 1 на 0;

3) к полученному прибавить 1.

Данная форма представления целого отрицательного числа называется дополнительным кодом. Использование дополнительного кода позволяет заменить операцию вычитания на операцию сложения уменьшаемого числа с дополнительным кодом вычитаемого.

Пример 3 Получить внутреннее представление целого отрицательного числа – 1607.

Решение. Внутреннее представление положительного числа:

0000 0110 0100 0111

обратный код: 1111 1001 1011 1000

результат прибавления 1: 1111 1001 1011 1001 – это внутреннее двоичное представление числа –1607. шестнадцатеричная форма F9B9.

Двоичные разряды в ячейке памяти нумеруются от 0 до k справа налево. Старший, k-й разряд во внутреннем представлении любого положительного числа равен нулю, отрицательного числа – единице. Поэтому этот разряд называется знаковым разрядом.

Вещественные числа

формат с плавающей точкой использует представление вещественного числа R в виде произведения мантиссы m на основание системы счисления q в некоторой целой степени p, которую называют порядком: R = m x q^p.

Представление числа в форме с плавающей точкой неоднозначно. Например, справедливы следующие равенства:

25.324 = 2.5324 х 10¹ = 0.0025324 х 10⁴ = 2532.4 х 10^-2=2.5324 Е+01 и т.п.

в ЭВМ используют нормализованное представление числа в форме с плавающей точкой. Мантисса в нормализованном представлении должна удовлетворять условию: иначе говоря, мантисса меньше единицы и первая значащая цифра – не ноль.

В памяти компьютера мантисса представляется как целое число, содержащее только значащие цифры (0 целых и запятая не хранятся). Следовательно, внутреннее представление вещественного числа сводится к представлению пары целых чисел: мантиссы и порядка.

В разных типах ЭВМ применяются различные варианты представления чисел в форме с плавающей точкой. Для примера рассмотрим внутреннее представление вещественного числа в 4-байтовой ячейке памяти.

В ячейке должна содержаться следующая информация о числе: знак числа, порядок и значащие цифры мантиссы.

+ маш. порядок

М А

Н Т И С

С А

1-й байт 2-й байт 3-й байт 4-й байт

в старшем бите 1-го байта хранится знак числа; 0 обозначает плюс, 1 – минус. Оставшиеся 7 бит первого байта содержат машинный порядок. В следующих трех байтах хранятся значащие цифры мантиссы (24 разряда).

В семи двоичных разрядах помещаются двоичные числа в диапазоне от 0 до 127 (в десятичной системе счисления). Всего 128 значений. Порядок, очевидно, может быть как положительным, так и отрицательным. разумно эти 128 значений разделить поровну между положительными и отрицательными значениями порядка: от –64 до 63.

Машинный порядок смещен относительно математического и имеет только положительные значения. Смещение выбирается так, чтобы минимальному математическому значению порядка соответствовал нуль.

Связь между машинным порядком (Мр) и математическим (р) в рассматриваемом случае выражается формулой:

Мр = р + 64.

Полученная формула записана в десятичной системе. В двоичной системе формула имеет вид: Мр₂ = р₂ + 100 0000₂.

Для записи внутреннего представления вещественного числа необходимо:

1) перевести модуль данного числа в двоичную систему счисления с 24 значащими цифрами;

2) нормализовать двоичное число;

3) найти машинный порядок в двоичной системе счисления;

4) учитывая знак числа, выписать его представление в 4-байтовом машинном слове.

Пример 4 записать внутреннее представление числа 250,1875 в форме с плавающей точкой.

Решение

1. Переведем его в двоичную систему счисления с 24 значащими цифрами: 250,1875₁₀ = 11111010, 0011000000000000₂.

2. Запишем в форме нормализованного двоичного числа с плавающей точкой: 0,111110100011000000000000 х 10₂¹⁰⁰⁰. Здесь мантисса 0,111110100011000000000000, основание системы счисления (2₁₀ = 10₂) и порядок (8₁₀ = 1000₂) записаны в двоичной системе.

3. Вычислим машинный порядок в двоичной системе счисления: Мр₂ = 1000 + 100 0000 = 100 1000.

4. Запишем представление числа в 4-байтовой ячейке памяти с учетом знака числа:

31 24 23 0

Шестнадцатеричная форма: 48FA3000.

Диапазон вещественных чисел значительно шире диапазона целых чисел. Положительные и отрицательные числа расположены симметрично относительно нуля. Следовательно, максимальное и минимальное числа равны между собой по модулю.

Наименьшее по абсолютной величине число равно нулю. Наибольшее по абсолютной величине число в форме с плавающей точкой – это число с самой большой мантиссой и самым большим порядком.

Для 4-байтового машинного слова таким числом будет:

0,111111111111111111111111 х 10₂^1111111.

После перевода в десятичную систему счисления получим:

(1 – 2^-24) х 2⁶³ = 10¹⁹.

Множество вещественных чисел, представимых в памяти компьютера в форме с плавающей точкой, является ограниченным и дискретным. Количество вещественных чисел, точно представимых в памяти компьютера, вычисляется по формуле: N = 2^t х (U – L + 1) +1. Здесь t – количество двоичных разрядов мантиссы; U – максимальное значение математического порядка; L – минимальное значение порядка. Для рассмотренного нами варианта (t = 24, U = 63, L = -64) получается

N = 2 146 683 548.

Примеры решения задач

Рассмотрим решения задач одного из вариантов контрольной работы.

Задача 1 Даны числа A₈ = 744, 56₈; A₁₆ = 5FA, 1B₁₆; А₂ = 101 001, 101 01_2. Выполнить перевод этих чисел в другие системы счисления.

При переводе чисел из двоичной системы счисления и обратно использовать таблицы триад и тетрад, связывающих восьмеричную, шестнадцатеричную и двоичную системы счисления.

А₈	А₂	А₁₆	А₂	А₁₆	А₂


				А(10)
				В(11)
				С(12)
				Д(13)
				Е(14)
				F(15)
	триады		тетрады		тетрады

Решение

а) A₈ ® A₂, если A₈ = 744, 56₈. Используя триады, получим

744, 56₈ = 111 100 100, 1011 1Ø₂.

б) A₁₆ ® A₂, если A₁₆ = 5FA, 1B₁₆.

Для решения используем тетрады:

5FA, 1B₁₆ = 0101 1111 1010, 0001 1011₂.

в) A₂ ® A₈, если А₂ = 101 001, 101 01₂.

Зная таблицу триад, имеем

101 001, 101 0 =51,52₈.

г) A₂ ® A₁₆, если A₂= 111 100 100, 101 11₂.

Из таблицы тетрад следует .

Задача 2 Перевести десятичное число в двоичную, восьмеричную, шестнадцатеричную системы, оставив 4 знака в дробной части.

А₁₀ ®А₂ ®А₈ ®А₁₆, если А₁₀ = 54,7.

Решение

Переведем сначала целую часть 54, разделив на соответствующее основание системы счисления, записав в итоге последовательно последнее частное и все остатки до первого включительно.

54 ë2 54₁₀=110110₂

54 27 ë2

0 26 13 ë2

1 12 6 ë2

1 6 3 ë2

0 2 1

54 ë8 54₁₀=66₈

48 6

54 ë16 54₁₀=36₁₆

48 3

_´0,7 16 ₊ 42 7 В_´11,2 16 _´3,2 16 _´3,2 16 3,2

_´0,7 8 _´5,6 8 _´4,8 8 _´6,4 8 3,2

Переведем дробную часть 0,7, умножив на соответствующее основание системы счисления дробные части результатов, записав в итоге целые части произведений от первого до четвертого результата включительно.

_´0,7

_´ 1,4

_´ 0,8

_´ 1,6

1,2

0,7₁₀=0,1011₂; 0,7₁₀=0,5463₈; 0,7₁₀=0,В333₁₆.

Таким образом, 54,7 = 110110, 1011₂ = 66,5463₈=36,В333₁₆.

Задача 3 Перевести указанные числа в десятичную систему счисления.

А₂ ®А₁₀, если А₂ = 1 101, 011₂.

Решение. Используем развернутую форму записи числа по разрядам:

А₈ ®А₁₀, если А₈ = 167,81₈.Рассуждая аналогично, получим:

А₁₆ ®А₁₀, если А₁₆ = АВ,1F₁₆.

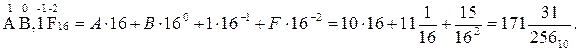
Задача 4 Дано уравнение x + y = z. Все числа записаны в восьмеричной системе счисления. х = 271,5₈ z = 462,3₈. Каково значение y₈?

Один из способов решения: переведем х₈ ® А₁₀, z₈ ®А₁₀, используя развернутую (поразрядную) запись числа.

х₈ =

z₈ =

y₈= z₈ – x₈ = .

_´0,75 8 6,0 0

Переведем 120,75₁₀ ® А₈.

120 ë8

8 15 ë8

40 8 1

40 7

120₁₀=170₈0,75₁₀=0,6₈

Таким образом, 120,75₁₀ = 170,6₈.

Ответ: y = 170,6₈.

Указание: можно решать, используя таблицы сложения в восьмеричной системе счисления.

Задача 5 В процессе преобразования графического файла количество цветов увеличилось с 64 до 4096. Как изменится информационный объем файла?

Решение. Известно, что информационный объем V=k×x, где k – количество символов, x бит – информационный объем одного символа алфавита.

Алфавит состоял из N₁ = 64 цветов, т.е. N₁ = Þ

х₁ = log₂64 = log₂2⁶ = 6 бит.

Для N₂ = 4096 имеем: N₂ = 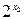Þ х₂ = log₂4096 = log₂2¹² = 12 бит.

Количество символов в обоих случаях не меняется по условию задачи, поэтому V₁=k×x₁, а V₂=k×x₂. Значит, .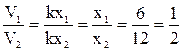

Вывод: информационный объем увеличился в два раза.

Задача 6. Сколько мегабайтов составит сообщение из 5000 символов 16-символьного алфавита?

Решение. Мощность алфавита n = 16, т.е. N = 2^x, х = log₂16 = 4 бита информационный объем одного символа. Тогда при k = 5000 символов.

V = x×k = 5000 × 4 = 20000 бит = байт = 2500 байт = Кбайт»

» 2,441Кбайт = Мбайт» 0,0023 Мбайт.

Ответ: 0,023 Мбайт

(известно, что 8бит = 1байт, 2¹⁰байт = 1Кбайт, 2¹⁰Кбайт = 1Мбайт,

2¹⁰Мбайт = 1Гбайт, 2¹⁰Гбайт = 1Тбайт).

Задача 7 Какой объем памяти необходим для хранения указанного текста?

Компьютер – это классно!

Используется 64-символьный алфавит.

Решение. Количество символов в тексте k = 22. Мощность алфавита n = 64, т.е. 2^x = N; х = log₂ N = log₂64 = 6 бит информационный объем одного символа алфавита. Тогда V_памяти = x×k = 6 × 22 = 132 бита.

Ответ: 132 бита.

Варианты заданий контрольной работы

1 вариант

1 Перевести число 15FC₁₆ в двоичную систему счисления.

2 Перевести смешанное число 1011101,10111₂ в восьмеричную систему.

3 Чему равно произведение в десятичной системе двух чисел 1011₂ и 7₁₀?

4 Чему равна сумма чисел в десятичной системе 774₈+654₈?

5 Сколько символов содержит сообщение, записанное с помощью 16-символьного алфавита, если объем его составил 1/16 Мбайта?

6 В процессе преобразования растрового графического файла количество цветов уменьшилось с 65536 до 256. Как изменится информационный объем файла?

7 Заполнить таблицу, показать процесс решения.

Система счисления


	16,5625
		19,B

8 Вычислить, показав процесс расчета. А) 11010₂+1101₂ Б) 11001₂ – 101₂ В) 1110₂ * 101₂ Г) 111₂: 10₂Д) 165₈ + 27₈

2 вариант

1 Перевести десятичное число 21,5 в двоичную и восьмеричную системы счисления, оставив 4 знака в дробной части.

2 Перевести числа 10101,01₂ и АВС₁₆ в десятичную систему счисления.

3 Чему равно произведение в десятичной системе двух чисел 757₈ и 101₂?

4 Дано уравнение N + X = M. Все числа записаны в шестнадцатеричной системе счисления. М = 18В0₁₆, N = 11С2₁₆. Тогда Х₁₆ равен…?

5 Размер дисплея 640*480 точек. Если в растровой графике используется 16 цветов, тогда для хранения данного изображения на диске нужен следующий минимальный объем памяти…?

6 Дано высказывание:Под один символ в памяти компьютера выделяется 8 битов. Оно истинно. Объем памяти, необходимый для хранения данной информации в памяти компьютера, составляет…?

7 Заполнить таблицу, показать процесс решения.

Система счисления


	26,5625
		29,B

8Вычислить, показав процесс расчета. А) 1010₂+110,1₂ Б) 11001₂ – 10101₂В) 1010₂ * 10,01₂ Г) 110,1₂: 10₂Д) 25₈ + 127₈

3 вариант

1 Перевести число 24А,9F₁₆в двоичную систему счисления.

2 Перевести числа 234,2₈ и 111,101₂в десятичную систему счисления.

3 Чему равно произведение в десятичной системе счисления двух чисел 1011,011₂ и 1014₈?

4 Чему равна сумма чисел в десятичной системе счисления 94А,В₁₆+1АС,F₁₆?

5 Сколько символов в использованном алфавите, если все сообщение содержит 2250 байтов, состоит из 3 страниц по 25 строк, в каждой строке по 60 символов?

6 В школьной библиотеке 16 стеллажей с книгами. На каждом стеллаже 32 полки. Библиотекарь сказал, что нужная книга находится на 5 стеллаже на третьей полке сверху. Какое количество информации передал клиенту библиотекарь?

7 Заполнить таблицу, показать процесс решения.

Система счисления


	36,5625
		69,B

8 Вычислить, показав процесс расчета. А) 110₂+10101₂ Б) 11001₂–1001₂В) 1110₂ * 100,1 Г) 11,01₂: 10₂ Д) 65₈ + 127₈

4 вариант

1 Перевести число АВС,1А₁₆в двоичную систему счисления.

2 Перевести числа 10101,01₂ и АС,А1₁₆в десятичную систему счисления.

3 Чему равно произведение в десятичной системе счисления двух чисел 10,01₈ и 10101,01₂?

4 Дано уравнение N + X = M. Все числа записаны в шестнадцатеричной системе счисления. М = 180В₁₆, N = 1С12₁₆. Тогда Х₁₆ равен…?

5 Сообщение, записанное буквами из 32-символьного алфавита, содержит 50 символов. Какой объем информации оно несет?

6 Два сообщения содержат одинаковое количество символов. Количество информации в первом тексте в 1,5 раза больше, чем во втором. Сколько символов содержат алфавиты (N₁, N₂), с помощью которых записаны сообщения, если известно, что число символов в каждом алфавите не превышает 10 и на каждый символ приходится целое число битов?

7 Заполнить таблицу, показать процесс решения.

Система счисления


	36,5625
		39,B

8 Вычислить, показав процесс расчета. А) 1010₂+11101₂ Б) 11001₂–10110₂В) 1010₂*10,01₂Г) 1001₂: 110₂Д) 365₈+227₈

5 вариант

1 Перевести число В1А,Е1₁₆в двоичную систему счисления.

2 Перевести числа 1АС,В₁₆ и 1101,001₂в десятичную систему счисления.

3 Чему равно произведение в десятичной системе счисления двух чисел 10111100,01₂ и 104₈?

4 Дано уравнение N+X=M. Все числа записаны в шестнадцатеричной системе счисления. М=АF1₁₆ и N=1ВС₁₆. Тогда Х₁₆ равен…?

5 Сообщение занимает 3 страницы и содержит 3/16 Кбайта информации. На каждой странице 256 символов. Какова мощность использованного алфавита?

6 Сообщение, что друг живет на 8 этаже, несет 3 бита информации. Сколько этажей в доме?

7 Заполнить таблицу, показать процесс решения.

Система счисления


	56,5625
		59,А

8 Вычислить, показав процесс расчета. А) 110₂+110,1₂ Б) 1101₂–100,1₂В) 110₂*1,001₂Г) 111,01₂:10₂Д) 165₈ + 127₈

6 вариант

1 Перевести число ВАС,1А₁₆ в двоичную систему счисления.

2 Перевести следующие числа 11001,11₂ и АВС₁₆в десятичную систему счисления.

3 Чему равно произведение в десятичной системе счисления двух чисел 32,12₈ и 101011,11₂?

4 Чему равна сумма чисел 747₈+564₈ в десятичной системе счисления?

5 Сколько символов содержит сообщение, записанное с помощью 8-символьного алфавита, если его объем составил 1/16часть Мбайта?

6 Два сообщения содержат одинаковое количество информации. Количество символов в первом тексте в 2,5 раза меньше, чем во втором. Сколько символов содержат алфавиты (N₁, N₂), с помощью которых записаны сообщения, если известно, что размер каждого алфавита не превышает 32 символов и на каждый символ приходится целое число битов?

7 Заполнить таблицу, показать процесс решения.

Система счисления


	46,5625
		49,B

8 Вычислить, показав процесс расчета. А) 110₂+101₂ Б) 11101₂ – 11001₂В) 1110₂ * 100,1₂ Г) 11,01₂: 101₂Д) 465₈ + 327₈

7 вариант

1 Перевести число 1А1,1Е₁₆в двоичную систему счисления.

2 Перевести числа 101101,01₂ и 623,4₈в десятичную систему счисления.

3 Чему равно произведение в десятичной системе счисления двух чисел 364₈ и 1А1,1₁₆?

4 Чему равна сумма чисел 10101110₂ и 11001101₂в десятичной системе счисления?

5 Сколько символов в строке сообщения, написанного 64-символьным алфавитом на 30 строках. Все сообщение содержит 8640 байтов информации и занимает 6 страниц.

6 Сообщение о том, что Петя живет во втором подъезде, несет 4 бита информации. Сколько подъездов в доме?

7 Заполнить таблицу, показать процесс решения.

Система счисления


	86,5625
		89,B

8 Вычислить, показав процесс расчета. А) 110₂+1001₂ Б) 1001₂–11001₂В) 1110₂*11001₂Г) 1001₂: 10₂Д) 265₈ + 127₈

8 вариант

1 Перевести число 456,7А₁₆в двоичную систему счисления.

2 Перевести следующие числа 101,4₈ и 101011,10₂в десятичную систему счисления.

3 Чему равно произведение в десятичной системе счисления двух чисел 56₁₆ и 10101,1₂?

4 Дано уравнение N+X=M. Все числа записаны в восьмеричной системе счисления. М =5647₈ и N =2711₈. Тогда Х₈ равен…?

5 Информационное сообщение объемом 3 кбайта содержит 3072 символа. Сколько символов содержит алфавит, при помощи которого было написано это сообщение?

6 Два сообщения содержат одинаковое количество символов. Количество информации в первом тексте в 1,5 раза больше, чем во втором. Сколько символов содержат алфавиты (N₁, N₂), с помощью которых записаны сообщения, если известно, что число символов в каждом алфавите не превышает 16 и на каждый символ приходится целое число битов?

7 Заполнить таблицу, показать процесс решения.

Система счисления


	46,625
		9,B

8 Вычислить, показав процесс расчета. А) 1110₂+1101₂ Б) 11101₂–10,01₂В) 110₂*10,01₂Г) 1111,01₂:10₂Д) 165₈+27₈

9 вариант

1 Перевести число 1А1,АЕ₁₆в двоичную систему счисления.

2 Перевести числа 456,7₁₆ и 11001,11₂в десятичную систему счисления.

3 Чему равно произведение в десятичной системе счисления двух чисел 1010,001111₂ и 432₁₀?

4 Чему равна сумма чисел в десятичной системе счисления 896₁₆+АВ1₁₆?

5 Сколько килобайтов составляет сообщение из 384 символов 8- символьного алфавита?

6 Для цветной картинки, составленной из 64 цветов в графическом мониторе 640*480, требуется объем видеопамяти в Кбайт….?

7 Заполнить таблицу, показать процесс решения.

Система счисления


	66,5625
		69,B

8 Вычислить, показав процесс расчета. А) 1110₂+110101₂ Б) 1101₂ – 100101₂В) 1110₂ * 100,1₂ Г) 1101₂: 101₂Д) 665₈ + 527₈

10 вариант

1 Перевести число А1В,1Е₁₆в двоичную систему счисления.

2 Перевести числа 456,7₈ и 11101,01₂в десятичную систему счисления.

3 Чему равно произведение в десятичной системе счисления двух чисел 101,4₈ и 2F,8₁₆?

4 Дано уравнение N + X = M. Все числа заданы в двоичной системе счисления. М = 110110₂ и N = 111110₂. Тогда Х₂ равен…?

5 Для записи текста использовался 256-символьный алфавит. Каждая страница содержит 30 строк и 50 символов в строке. Какой объем информации содержат 5 страниц текста?

6 Письмо написано 32-символьным алфавитом, другое письмо 64- символьным алфавитом. В первом - 80 символов, во втором – 70 символов. Какое письмо по объему информации больше?

7 Заполнить таблицу, показать процесс решения.

Система счисления


	76,5625
		79,B

8.Вычислить, показав процесс расчета. А) 110₂+1101₂ Б) 11001₂ – 11001₂В) 1110₂ * 0,1001₂ Г) 111101₂: 110₂Д) 465₈ + 527₈

СОДЕРЖАНИЕ

1 ПРЕДСТАВЛЕНИЕ ЧИСЛОВОЙ ИНФОРМАЦИИ.. 3

2 измерение информации.. 14

3 Представление информации в компьютере. 19

4 Примеры решения задач. 23

5 Варианты заданий КонтролЬной работы.. 26

Список литературы.. 31

Список литературы

1 Акулов, О. А. Информатика: базовый курс [Текст]/ О. А. Акулов, Н. В. Медведев. – М.: Омега-Л, 2004. – 552 с.

2 Информатика [Текст]: Задачник-практикум: в 2 т. / под ред. И. Г. Семакина, Е. К. Хеннера. – М.: Бином. Лаборатория Знаний, 2002. – 303 с.

3 Босова, Л. Л. Арифметические и логические основы ЭВМ [Текст] / Л. Л. Босова. – М.: Информатика и образование, 2000. – 208 с.

Сысолятина Лидия Геннадьевна

Бекишева Марина Борисовна

⇐ Предыдущая 1 23

Воспользуйтесь поиском по сайту: