 |
Образец выполнения контрольной работы.
|
|
|
|
Задание 1.
Даны вершины ∆АВС: А(2;5), B(14;-4), C(18;18). Требуется найти:
1) длины сторон AB и AC, их уравнения и угловые коэффициент;
2) величину угла A в градусах с точностью до двух знаков;
3) уравнение биссектрисы AK угла A;
4) точку F пересечения медиан треугольника ABC;
5) уравнение высоты CN и точку N ее пересечения со стороной AB;
6) уравнение прямой L, проходящей через вершину B параллельно стороне AC и ее точку пересечения с высотой CN;
7) координаты точки D, симметричной точке C относительно точки T и лежащей на медиане CT;
8) вычислить площадь четырехугольника ABCD.
9) сделать чертеж.
Решение.
1)Длину отрезка АВ найдем по формуле:

Так как  , то
, то
 .
.
Уравнение прямой АВ найдем по формуле: (АВ):  .
.

Угловой коэффициент прямой АВ равен:  .
.
Аналогично, 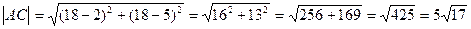 ,
,


Угловой коэффициент прямой АС равен: 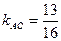 .
.
2) Вершину угла А рассмотрим как угол между прямыми АС и АВ.
Найдем ее по формуле:  , где
, где  .
.
Так как 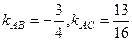 , то
, то 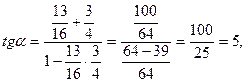
Тогда 

3) Уравнение биссектрисы AK угла A найдем по формуле:  , где
, где  =0 и
=0 и  =0 – уравнения сторон АВ и АС угла А.
=0 – уравнения сторон АВ и АС угла А.
Так как  и
и 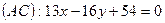 , то
, то 
или  или
или  .
.
Итак, 
4) Точку F пересечения медиан треугольника АВС найдем, решив совместно систему уравнений любых двух медиан треугольника. Для этого найдем уравнения медиан AM и BE, проведенных из вершин А и В.
Так как АМ медиана, то точка М делит сторону ВС пополам. Тогда координаты точки М найдем по формуле:  .
.
Подставив координаты точек В и С в эти формулы, получим
 . Итак, М(16;7).
. Итак, М(16;7).
Аналогично найдем координаты точки Е, которая делит сторону АС пополам:
 . Итак, Е(10;11.5).
. Итак, Е(10;11.5).
Воспользовавшись формулой  , найдем уравнения медиан АМ и ВЕ.
, найдем уравнения медиан АМ и ВЕ.
Имеем,  ;
;
 .
.
Найдем координаты точки F, решив систему уравнений:

Итак, 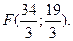
5) Найдем уравнение высоты CN.
Так как  , то
, то 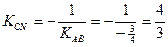 , где
, где  - угловые коэффициенты прямых СN и АВ соответственно. В общем виде уравнение CN имеет вид:
- угловые коэффициенты прямых СN и АВ соответственно. В общем виде уравнение CN имеет вид:  . Чтобы найти b, подставим координаты точки C в уравнение CN:
. Чтобы найти b, подставим координаты точки C в уравнение CN: 
|
|
|
Итак, уравнение (CN):  или 4x-3y-18=0.
или 4x-3y-18=0.
Координаты точки N как точку пересечения прямых AB и CN найдем, решив следующую систему уравнений:

Итак, точка N имеет координаты (6;2)
6) Т.к. прямая L параллельна стороне АC, то  и уравнение прямой L имеет вид:
и уравнение прямой L имеет вид:  . Значение b найдем из того, что L проходит через вершину В треугольника АВС:
. Значение b найдем из того, что L проходит через вершину В треугольника АВС:  .
.
Итак, уравнение прямой L имеет вид:  или
или  .
.
Найдем координаты точки R пересечения прямых L и CN. Для этого решим следующую систему уравнений: 
 .
.
Имеем, R(-18;-30).
7) Так как СТ–медиана треугольника АВС, то точка Т делит сторону АВ пополам, а тогда ее координаты равны:
 , следовательно, Т(8;0.5).
, следовательно, Т(8;0.5).
Так как точка D симметрична точке С относительно точки Т, то точка Т делит отрезок. CD пополам. А тогда  .
.
Имеем,  . Итак, D(-2;-17).
. Итак, D(-2;-17).
8) Найдем площадь четырехугольника AСBD. Этот четырехугольник есть параллелограмм. Действительно, ∆ATC=∆BTD, т.к. АТ=ТВ(СТ-медиана), СТ=ТD(Т-делит отрезок пополам),  (внутренний угол). Следовательно, АС=BD и ACIIBD(
(внутренний угол). Следовательно, АС=BD и ACIIBD( -как внутренние накрест лежащие, образованные параллельными прямыми АС и BD и секущей АВ). Тогда площадь параллелограмма ACBD определим как две площади треугольника АВС. Имеем, что
-как внутренние накрест лежащие, образованные параллельными прямыми АС и BD и секущей АВ). Тогда площадь параллелограмма ACBD определим как две площади треугольника АВС. Имеем, что  . Так как
. Так как  и
и  , то
, то  . А тогда
. А тогда 
Определим также площадь четырехугольника ACBD, пользуясь понятием определителя, т.е. формулой:
 .
.
Имеем,


9) Построим треугольник АВС и все прямые и точки:
 Ответ: 1)
Ответ: 1)  ;
;  ;
;  ;
; 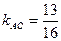 ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5) 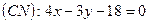 ; N(6;2); 6)
; N(6;2); 6)  ; R(-18;-30);
; R(-18;-30);
7) D(-2;-17); 8)  .
.
Задание 2.
Даны точки плоскости A(-4;-4), B(-3;3), C(4;2).Требуется:
1) составить уравнение окружности, проходящей через эти точки, определить координаты центра N и величину R радиуса окружности;
2) написать уравнение эллипса, проходящего через точки B и C, найти полуоси, фокусы, эксцентриситет;
3) построить точки и кривые в системе координат.
Решение.
|
|
|
1) Пусть точки А, В, С лежат на одной окружности, центр которой находится в точке  . Тогда они расположены на одном расстоянии от центра окружности, т.е. AN=BN=CN=R. Определим эти величины, как расстояние между двумя точками по формуле:
. Тогда они расположены на одном расстоянии от центра окружности, т.е. AN=BN=CN=R. Определим эти величины, как расстояние между двумя точками по формуле:  .
.
Имеем,

Решим следующую систему уравнений:





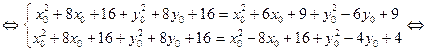


Следовательно, центр окружности имеет координаты: N(0;-1). Радиус определим, подставив координаты точки N в любое из вычисленных расстояний, например, AN=R:
 .
.
Таким образом, окружность радиуса R=5 с центром в точке N(0;-1) и проходящая через точки А, В, С имеет вид:  или
или  (воспользовались формулой
(воспользовались формулой  ).
).
2) Каноническое уравнение эллипса имеет вид:  , где
, где 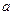 и
и  -полуоси эллипса.
-полуоси эллипса.
Так как точки В и С принадлежат эллипсу, то:

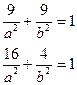


Уравнение эллипса примет вид:  или
или  .
.
Полуоси эллипса:  ,
,  .
.
Фокусы эллипса имеют координаты:  , где с-расстояние от центра эллипса, расположенного в начале координат (0;0), до фокуса; эта величина равна
, где с-расстояние от центра эллипса, расположенного в начале координат (0;0), до фокуса; эта величина равна  .
.
Итак, 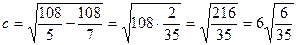 , а тогда
, а тогда 
Эксцентриситет эллипса найдем по формуле:  . Имеем,
. Имеем,  .
.
Замечаем, что  , это говорит о том, что рассматриваемая нами кривая второго порядка является эллипс.
, это говорит о том, что рассматриваемая нами кривая второго порядка является эллипс.
3) Построим окружность и эллипс на одной системе координат:
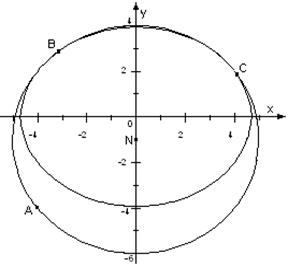
Ответ: 1)  -уравнение окружности с центром N(0;-1) и радиуса R=5;
-уравнение окружности с центром N(0;-1) и радиуса R=5;
2)  -уравнение эллипса; полуоси эллипса:
-уравнение эллипса; полуоси эллипса:  ;
; 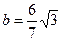 ;
;
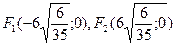 -фокусы эллипса;
-фокусы эллипса;  -эксцентриситет эллипса.
-эксцентриситет эллипса.
Задание 3.
Решить систему линейных уравнений с помощью определителей:
 .
.
Решение.
Найдем определитель системы уравнений составленный из коэффициентов при неизвестных:

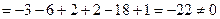 .
.
Так как  , то система уравнений имеет единственное решение.
, то система уравнений имеет единственное решение.
Найдем определитель  , который получим из
, который получим из  путем замены столбца при переменной x столбцом свободных членов:
путем замены столбца при переменной x столбцом свободных членов:

 .
.
Аналогично найдем определители  и
и  .
.

 ;
;

 .
.
Используя правило Крамера, найдем решение системы уравнений:



Проверка.

Итак, решение системы 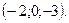

Ответ: 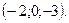
Задание 4.
Решить систему линейных уравнений методом Гаусса:

Решение.
Рассмотрим расширенную матрицу системы уравнений:
 .
.
Используя элементарные преобразования, приведем матрицу к ступенчатому виду:

|
от последней матрицы перейдем к системе уравнений:

Проверка.

Итак, решение системы  .
.
Ответ:  .
.
Задание 5.
Представить систему линейных уравнений в матричной форме и решить систему с помощью обратной матрицы; пользуясь правилом умножения матриц, показать, что произведение матрицы системы на обратную ей матрицу равно единичной матрице E:
|
|
|

Решение.
Запишем данную систему линейных уравнений в матричной форме: AX=B, где
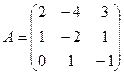 ;
; 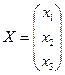 ;
;  .
.
Для решения системы воспользуемся следующей формулой: 
Найдем определитель матрицы А:
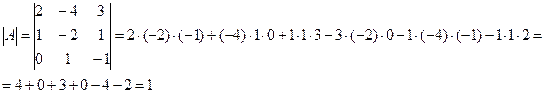
Так как  , то существует обратная матрица
, то существует обратная матрица  , и, следовательно, система линейных уравнений имеет единственное решение.
, и, следовательно, система линейных уравнений имеет единственное решение.
Найдем обратную матрицу по формуле:
 , где
, где  - определитель матрицы A,
- определитель матрицы A,
Ai j-алгебраические дополнения для элементов aij матрицы A
Найдем алгебраические дополнения:
A 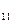 =
=  =2-1=1; A
=2-1=1; A  =
= 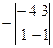 =-(4(-3))=-1;
=-(4(-3))=-1;
A  =
=  =-4+6=2; A
=-4+6=2; A 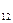 =
=  -(-1-0)=1;
-(-1-0)=1;
A  =
=  =-2-0=-2; A
=-2-0=-2; A 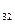 =
=  =-(2-3)=1;
=-(2-3)=1;
A  =
=  =1- 0=1; A
=1- 0=1; A  =
=  =-(2-0)=-2;
=-(2-0)=-2;
A 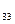 =
=  =-4+4=0.
=-4+4=0.
Обратная матрица имеет вид: 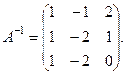 .
.
Сделаем проверку:
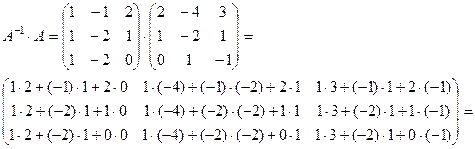

Найдем решение системы уравнений:
 .
.
Ответ: (-2;1;3).
Задание 6.
Даны координаты вершин пирамиды ABCD: А(2;1;2), В(-2;0;1), С(3;1;1), D(4;2;0). Требуется:
1) записать векторы  в системе орт и найти модули этих векторов;
в системе орт и найти модули этих векторов;
2) найти угол между векторами 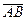 и
и  в градусах с точностью до двух знаков после запятой;
в градусах с точностью до двух знаков после запятой;
3) найти проекцию вектора 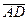 на вектор
на вектор 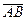 ;
;
4) вычислить площадь грани ABC;
5) найти объем пирамиды ABCD.
Решение.
1) Если 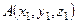 и
и  , то вектор
, то вектор 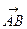 имеет координаты:
имеет координаты: 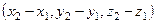 .
.
Следовательно,

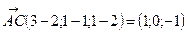

В системе орт эти вектора имеют вид:
 ;
;  ;
;  .
.
Длину вектора 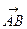 найдем по формуле:
найдем по формуле:  . Имеем
. Имеем  ,
,  ,
,  .
.
2) Если 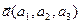 и
и  и a-угол между этими векторами, то этот угол можно определить по формуле:
и a-угол между этими векторами, то этот угол можно определить по формуле:  .
.
Тогда 

Получаем 
3) Проекцию вектора  на вектор
на вектор  найдем по формуле:
найдем по формуле:  , где
, где  -скалярное произведение векторов
-скалярное произведение векторов  и
и  . Так как
. Так как  ,
,  , то
, то  . А тогда
. А тогда 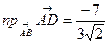 .
.
4) Площадь грани АВС найдем по формуле:
 ,
,
где  ,
, 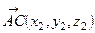 . Имеем
. Имеем  ,
,  . Тогда:
. Тогда:
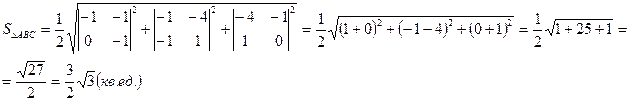 5) Из школьного курса известно, что
5) Из школьного курса известно, что  , тогда
, тогда
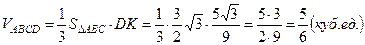 .
.
С другой стороны  , где
, где  ,
, 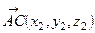 ,
,  .
.
Имеем,  ,
,  ,
,  ,
, 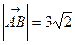 ,
,  ,
, 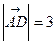 .
.
Тогда 
Ответ: 1)  ;
;  ;
;  ;
; 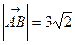 ;
;  ;
; 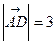 ;
;
2)  ; 3)
; 3) 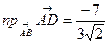 ; 4)
; 4)  ; 5)
; 5) 
Задание 7.
Даны координаты точек A(6;2;8), B(10;4;4), C(7;1;4).
Требуется:
1) составить канонические уравнения прямой AB;
2) составить уравнение плоскости Q, проходящей через точку C перпендикулярно прямой AB;
3) найти точку пересечения прямой AB с плоскостью Q;
|
|
|
4) вычислить расстояние от точки C до прямой AB;
5) найти точку D, симметричную точке С относительно прямой АВ.
Решение.
1)Прямая, проходящая через две точки  и
и 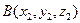 пространства, может быть представлена каноническими уравнениями:
пространства, может быть представлена каноническими уравнениями:  .
.
Так как А(6;2;8) и В(10;4;4), то  или
или  .
.
Итак, 
2) Направляющий вектор прямой АВ имеет вид: 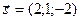 . Известно, что если прямая
. Известно, что если прямая
 перпендикулярна плоскости
перпендикулярна плоскости  , то
, то  . Так как плоскость Q проходит через точку С, то ее уравнение можно найти, используя уравнение плоскости, проходящей через данную точку
. Так как плоскость Q проходит через точку С, то ее уравнение можно найти, используя уравнение плоскости, проходящей через данную точку 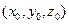 :
:
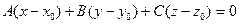 .
.
Тогда 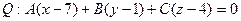 . Так как
. Так как  , то
, то  и, следовательно, уравнение плоскости Q примет вид:
и, следовательно, уравнение плоскости Q примет вид:  или
или
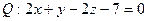 .
.
3) Запишем уравнение прямой АВ в параметрическом виде. Пусть 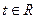 -параметр, тогда
-параметр, тогда  . Подставим выражения для x, y, z в уравнение плоскости
. Подставим выражения для x, y, z в уравнение плоскости 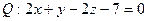 и найдем значение параметра t, зная который определим координаты точки Kпересечения прямой AB с плоскостью
и найдем значение параметра t, зная который определим координаты точки Kпересечения прямой AB с плоскостью  .
.
Имеем:  .
.
Тогда точка K имеет координаты (8;3;6).
4) Так как прямая АВ перпендикулярна плоскости  , которая проходит через точку С, то расстояние от точки С до прямой АВ найдем как расстояние между точками С и K по формуле:
, которая проходит через точку С, то расстояние от точки С до прямой АВ найдем как расстояние между точками С и K по формуле: 
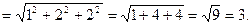
5) Так как точка D симметрична точке С относительно прямой АВ, то прямая АВ перпендикулярна прямой CD, а, следовательно, CK=DK, т.е. точка K делит отрезок CD пополам. А тогда  ;
;  ;
;  .
.
Откуда  ;
;  ;
;  . Итак, точка D имеет координаты
. Итак, точка D имеет координаты  ;
;  ;
;  или D(9;5;8).
или D(9;5;8).
Ответ: 1) 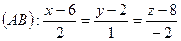 ; 2)
; 2) 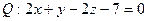 ; 3) K(8;3;6); 4) D(9;5;8).
; 3) K(8;3;6); 4) D(9;5;8).
Задание 8.
Прямая линия задана в виде пересечения двух плоскостей. Написать канонические уравнения этой прямой и найти точку P, симметричную точке N(2;-1;4) относительно этой прямой.

Решение.
Чтобы найти канонические уравнения прямой, необходимо знать координаты какой-либо точки, лежащей на этой прямой, и координаты направляющего вектора этой прямой.
Прямая задана в виде системы двух уравнений с тремя неизвестными x, y, z. Такая система имеет бесконечное множество решений. Найдем одно из них. Придадим одной из переменных определенное значение, например, z=0. Тогда получим систему двух уравнений с двумя неизвестными x и y. Решим ее:
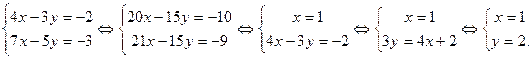
Таким образом, одна из точек прямой имеет координаты (1;2;0). Координаты направляющего вектора определим как координаты вектора, представляющего собой векторное произведение нормальных векторов заданных плоскостей:  и
и 

Итак, направляющий вектор  данной прямой имеет координаты: (19;26;1).
данной прямой имеет координаты: (19;26;1).
Каноническое уравнение прямой L можно записать в виде:
 , где
, где 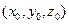 -координаты точки, принадлежащей данной прямой и
-координаты точки, принадлежащей данной прямой и  - направляющий вектор этой прямой.
- направляющий вектор этой прямой.
Следовательно, прямая имеет вид: 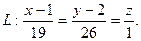
Найдем координаты точки P симметричной точке N относительно прямой L. Точка T лежит на прямой L и делит отрезок PN пополам. Тогда координаты точки P найдем по формулам: 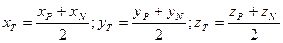 . (1)
. (1)
|
|
|
Прямая TN перпендикулярна прямой L, следовательно, их направляющие вектора  и
и  также перпендикулярны. А это означает, что
также перпендикулярны. А это означает, что  , т.е.
, т.е. 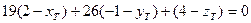 или
или  . (2)
. (2)
Так как точка T принадлежит прямой L, то ее координаты, подставленные в уравнение прямой L, обращают его в верное тождество:  Пусть эти отношения равны некоторому параметру t, тогда
Пусть эти отношения равны некоторому параметру t, тогда  .
.
Подставим выражения для x, y, z в уравнение (2), получим

Итак, T имеет координаты:  .
.  .
.
Из формулы (1) следует, что координаты точки P вычислим по формуле:
 . Имеем,
. Имеем,  . Тогда
. Тогда  .
.
Ответ:  ;
;  .
.
Задание 9.
Найти пределы функций:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  .
.
Решение.
1) 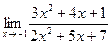 .
.
Подставим в функцию, стоящую под пределом, вместо x значение -1. Получим:

2)  .
.
При x=2 и знаменатель, и числитель функции f(x)=  обращаются в нуль:
обращаются в нуль:  и
и  ,
,  откуда получаем неопределенность вида
откуда получаем неопределенность вида 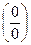 . Чтобы раскрыть неопределенность, разложим числитель и знаменатель на множители. Найдем корни числителя:
. Чтобы раскрыть неопределенность, разложим числитель и знаменатель на множители. Найдем корни числителя:

 ;
; 
 ;
;
корни знаменателя:
 ;
;  ;
; 

Итак, 

3)  ;
;
Подставляя  в функцию
в функцию  получаем неопределенность вида
получаем неопределенность вида  . Чтобы ее раскрыть, вынесем за скобки в числителе и знаменателе многочлены наивысшей степени. Получим:
. Чтобы ее раскрыть, вынесем за скобки в числителе и знаменателе многочлены наивысшей степени. Получим:
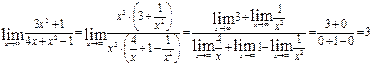
так как при 
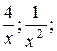 - бесконечно малы.
- бесконечно малы.
4)  .
.
При х=-2 числитель и знаменатель функции  обращается в нуль. Имеем неопределенность
обращается в нуль. Имеем неопределенность 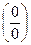 . Для ее раскрытия умножим числитель и знаменатель дроби на
. Для ее раскрытия умножим числитель и знаменатель дроби на 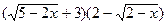 и выполним необходимые преобразования:
и выполним необходимые преобразования:

5) 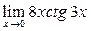 ;
;
Под знаком предела при  имеем неопределенность
имеем неопределенность  Преобразуем функцию
Преобразуем функцию  так, чтобы можно было использовать первый замечательный предел:
так, чтобы можно было использовать первый замечательный предел:  .
.

6)  .
.
Под знаком предела при 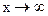 имеем неопределенность
имеем неопределенность  . Преобразуем функцию так, чтобы можно было использовать формулу
. Преобразуем функцию так, чтобы можно было использовать формулу  . Разделим числитель и знаменатель дроби на 5х и выполним необходимые преобразования:
. Разделим числитель и знаменатель дроби на 5х и выполним необходимые преобразования:

Ответ: 1) 0; 2)  ; 3) 3; 4)
; 3) 3; 4)  5)
5)  6)
6) 
Задание 10.
Найдите производные 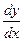 заданных функций.
заданных функций.
1) 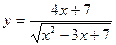 ; 2)
; 2) 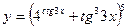 ; 3)
; 3)  ;
;
4) 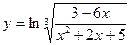 ; 5)
; 5) 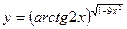 ; 6)
; 6) 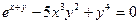 ; 7)
; 7)  .
.
Решение.
1) 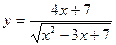 .
.
Найдем производную функции, используя правила дифференцирования:
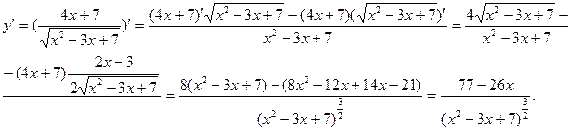
Использованы формулы:  ;
;  ;
; 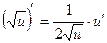 .
.
2) 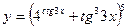 .
.
Найдем производную функции, используя правила дифференцирования:
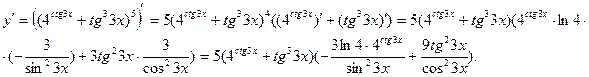
Использованы формулы:  ;
;  ;
;  ;
;
 ;
;  .
.
3)  .
.
Найдем производную функции, используя правила дифференцирования:

Использованы формулы:  ;
;  ;
; 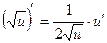 .
.
4) 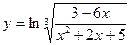 .
.
Найдем производную функции, используя правила дифференцирования. Для этого представим функцию в следующем в виде:
 .
.
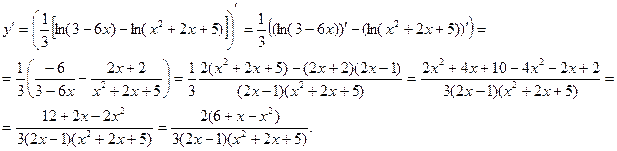
Использованы формулы:  ;
;  ;
;  .
.
5) 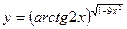 .
.
Найдем производную функции, используя правила дифференцирования:
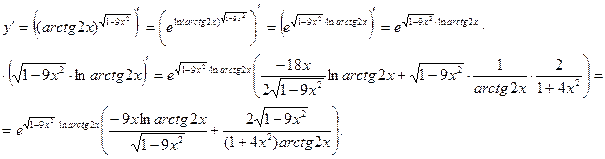
Использованы формулы:  ;
;  ;
;  ;
; 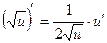 ;
;
 ;
;  .
.
6) 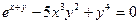 .
.
Так как функция задана неявно, то, для нахождения производной данной функции, возьмем производную обеих частей равенства:

Использованы формулы:  ;
;  ;
;  .
.
7)  .
.
Данная функция задана параметрически. Производную функции y(x) найдем по формуле:
 . Имеем,
. Имеем,  ;
; 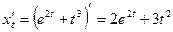 .
.
Тогда  .
.
Использованы формулы:  ;
;  ;
;  .
.
Задание 11.
Дана функция y=f(x) и значения аргумента x1 и x2. Требуется найти приближенное значение функции при x=x2, исходя из ее точного значения при x=x1, заменяя полное приращение функции ее дифференциалом:
1)  ; 2)
; 2) 
Решение.
Приближенное значение функции в точке x=x2 найдем, воспользовавшись формулой:  , где
, где  .
.
1)  .
.
Вычислим значение функции в точке x1=2:  .
.
Найдем производную функции  и вычислим ее значение в точке x1:
и вычислим ее значение в точке x1:


Тогда 
2) 
Вычислим значение функции в точке x1=0°: 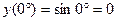 .
.
Найдем производную функции 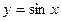 и вычислим ее значение в точке x1:
и вычислим ее значение в точке x1:
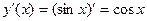 ;
; 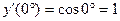 ;
;


