 |
Анализ парных взаимосвязей
|
|
|
|
Анализ парных взаимосвязей проводится в тех случаях, когда исследователя интересует вопрос о влиянии одной переменной на другую. При проведении анализа необходимо учитывать следующее:
1) одна переменная независима, и исследователи убеждены, что от неё зависит вторая переменная;
2) независимые переменные используются для того, чтобы предсказать или объяснить зависимые переменные, такие как объем продаж или доля рынка, принадлежащая предприятию;
3) если одна переменная является причиной изменения другой, то для принятия маркетингового решения необходимо изучить сущность статистической взаимосвязи между переменными;
4) задача измерения тесноты связи ставится не только по отношению к количественным, но и к качественным признакам.
Типичными независимыми переменными в маркетинге являются такие факторы, как цена продукта, затраты на рекламу или количество розничных продавцов/
Рассмотрим возможные случаи измерения связи между двумя признаками.
1. Альтернативная вариация признаков
Наиболее распространенными статистическими показателями, которые используются для измерения связи между такими признаками, являются коэффициенты ассоциации и контингенции. Например, при обследовании эффективности рекламных мероприятий по продвижению шампуней отечественного производства изучался вопрос о связи между проведением рекламных кампаний предприятиями-производителями и увеличением объема продаж. Можно предположить, что объем продаж увеличился у тех предприятий, которые проводили рекламные кампании. Для измерения этой связи составим двумерную матрицу (таблица 2.3).
Таблица 2.3 – Взаимосвязь между двумя альтернативными признаками
|
|
|
| Группы предприятий | Изменение объема продаж | Итого | |
| Увеличился | Не увеличился | ||
| Проводили рекламную кампанию | 78 (а) | 22 (b) | |
| Не проводили рекламную кампанию | 32 (c) | 68 (d) | |
| Итого |
Коэффициенты ассоциации (А) и контингенции (К) рассчитываются по формулам:
(15)
(16)
Подставив значения в формулы 20 и 21, получим:
А 
= 0, 7656
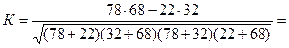0,4623
Связь считается подтверждённой, если А > 0.5; К > 0.3. Следовательно, проведение рекламных кампаний по продвижению шампуней приводит к увеличению объёма продаж предприятий-производителей.
Вариация качественных, но не альтернативных признаков
Если исходные данные представлены в таблице, в которой три и более ряда, то для определения тесноты связи между этими признаками используются коэффициенты взаимной сопряжённости Пирсона (С):
(17),
где 
Рассмотрим пример расчёта коэффициента взаимной сопряженности Пирсона для исследования взаимосвязи между воспринимаемой покупателями ценой на красивую фигню и намерением купить ее. Исходные данные для расчета представлены в таблице 2.4.
Таблица 2.4 – Расчёт коэффициента взаимной сопряженности Пирсона
| Воспринимаемая потребителями цена | Намерение купить | Всего | |||
| Определённо куплю | Вероятно, куплю | Вероятно, не куплю | Определённо не куплю | ||
| Очень дорого | |||||
| Дорого | |||||
| Нормально | |||||
| Дёшево | |||||
| Очень дёшево | |||||
| Всего |
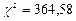
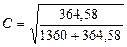= 0,46
Для подтверждения взаимосвязи коэффициент взаимной сопряженности Пирсона должен быть не меньше 0,5. В нашем случае связь между двумя изучаемыми признаками не подтверждается. Это означает, что намерение купить продукт не связано с восприятием цены на него.
|
|
|
