Предельная теорема Пуассона. Локальная и интегральная теоремы Муавра-Лапласа.

Предельная теорема Пуассона
Пусть число экспериментов Бернулли велико (n → ∞), а вероятность наступления события A в каждом испытании очень мала (p → 0, p < 0,1), тогда вероятность того, что событие A появится в серии из n испытаний ровно m раз, приближенно равна

(m =,2,1,0...), где произведение a = n ⋅ p = const.

Локальная теорема Лапласа. Если вероятность p появления события A в каждом испытании постоянна и отлична от нуля и единицы (0 < p < 1), то вероятность того, что событие A появится в серии из n испытаний ровно m раз приближенно равна (тем точнее, чем больше n) значению функции:

Функция ϕ(x) является четной функцией, то есть ϕ(– x) = ϕ(x), для всех x ≥ 4 принимается ϕ(x) = 0. Таким образом, вероятность того, что событие A появится в n независимых испытаниях ровно m раз, приближенно равна:

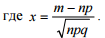
Интегральная теорема Лапласа. Если вероятность p наступления со- бытия A в каждом испытании постоянна и отлична от нуля и единицы (0 < p < 1), то вероятность того, что событие A появится в серии из n испытаний от k₁ до k₂ раз, приближенно равна:

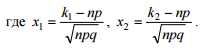
11. Понятие одномерной случайной величины (СВ)
Случайной величиной называют переменную величину, которая в зависимости от исхода испытания принимает значения, зависящие от случая. Случайные величины принято обозначать прописными буквами латин- ского алфавита: X, Y, Z, …, либо буквами греческого алфавита: ξ, η, θ, …, а их значения – строчными буквами латинского алфавита: x, y, z.
12. Закон распределения СВ
законом распределения случайной величины X называется любое соотношение, устанавливающее связь между возможными значениями этой случайной величины и соответствующими им вероятностями.
Законом распределения дискретной случайной величины называется соответствие между значениями х1, х2,х3.. этой величины и их вероятностями р1,р2,р3,...
Закон распределения дискретной случайной величины может быть задан с помощью формул или таблично.
Для полного описания исследуемого вероятностного эксперимента недостаточно задать только пространство элементарных событий Ω. К этому необходимо добавить также: а) для дискретной случайной величины – правило, сопоставляющее ка- ждому возможному значению случайной величины хi вероятность того, что случайная величина X примет в результате эксперимента это значение:
б) для непрерывной случайной величины – правило, позволяющее поставить в соответствие любой измеримой области ∆X возможных значений случайной величины X вероятность попадания значения случайной величины в эту область:

13. Функция распределения СВ и ее свойства
Универсальным способом задания закона распределения произвольной случайной величины является функция распределения.
Функцией распределения F(x) случайной величины ξ в точке x называется вероятность того, что величина ξ примет значение меньше x, т. е. функция распределения определяет вероятность события {ξ < x}:
F(x) = P(ξ < x).
Функция распределения произвольной случайной величины ξ обладает свойствами:
Свойство 1. F(x) ≥ 0, т. е. функция распределения – неотрицательная функция.
Свойство 2. F(−∞) = 0.
Свойство 3. F(∞) =1.
Свойство 4. Если x₁ < x₂, то F (x₁) ≤ F (x₂), т. е. функция распределения – неубывающая функция.
Свойство 5. Если, x₁ < x₂ то P(x₁ ≤ ξ < x₂) = F (x₁) − F (x₂), т. е. вероятность того, что случайная величина примет значение, принадлежащее полуинтервалу [ х₁,х₂), равна приращению функции распределения на этом полуинтервале.
Свойство 6. F(x −)0 = F(x), т. е. функция распределения непрерывна слева.

14. Функция плотности распределения СВ и ее свойства.

Плотностью распределения вероятностей непрерывной случайной величины X в точке x называется производная ее функции распределения в этой точке: f(x) = F ′(x).
По своему смыслу значения функции f(x) пропорциональны вероятности того, что исследуемая случайная величина примет значение где-то в непосредственной близости от точки x. Функция плотности распределения f(x), как и функция распределения F(x), является одной из форм задания закона распределения, но она применима только для непрерывных случайных величин. Функцию плотности распределения вероятностей f(x) еще называют дифференциальной функцией распределения, тогда как функцию распределения F(x) называют, соответственно, интегральной функцией распределения.
Свойство 1. Плотность распределения вероятностей – неотрицательная функция: f(x) ≥ 0. Кривая распределения лежит не ниже оси абсцисс
Свойство 2. Вероятность попадания значения случайной величины на участок от α до β определяется по формуле: эта вероятность равна площади криволинейной трапеции, ограниченной кривой f(x), осью Ох и прямыми x = α и x = β
Свойство 3 площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице
В частности, если все возможные значения случайной величины принадлежат отрезку [a, b], то:

Свойство 4. Функция распределения F(x) может быть найдена по известной функции плотности распределения следующим образом: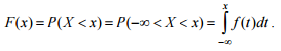

15. Числовые характеристики СВ. Математическое ожидание, дисперсия, мода, медиана, среднеквадратическое отклонение, коэффициент асимметрии, коэффициент эксцесса.

Характеристики, выражающие в сжатой форме наиболее существенные особенности распределения случайной величины, называются числовыми характеристиками случайной величины.
Математическое ожидание характеризует среднее значение случайной величины, вокруг которого группируются все ее значения. Термин «математическое ожидание» связан с начальным периодом развития теории вероятностей, когда она развивалась на примерах и задачах азартных игр и игрока интересовал средний выигрыш, то есть среднее значение ожидаемого выигрыша. Для дискретных и непрерывных случайных величин математическое ожидание вычисляется, соответственно, по формулам:

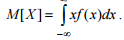
Свойства математического ожидания:
а) математическое ожидание постоянной величины равно этой постоянной: M[C] = C;
б) постоянный множитель можно выносить за знак математического ожидания: M[CX] = C M[X];
в) математическое ожидание алгебраической суммы конечного числа случайных величин равно алгебраической сумме их математических ожиданий. Например, для трех случайных величин X₁, X₂, X₃ M[X₁ ± X₂ ± X₃] = M[X₁] ± M[X₂] ± M[X₃];
г) если P(α ≤ Х < β)=1, то M[X] ∈[α;β], то есть математическое ожидание произвольной случайной величины X принадлежит интервалу между минимальным и максимальным возможными значениями случайной величины X;
д) математическое ожидание произведения конечного числа независимых случайных величин равно произведению их математических ожиданий. Напр., для трех независимых случайных величин X₁, X₂, X₃ M[X₁ X₂ X₃] = M[X₁] M[X₂] M[X₃].
Дисперсия является мерой рассеивания значений случайной величины относительно ее математического ожидания. Для дискретных и непрерывных случайных величин дисперсию можно вычислить по формулам:

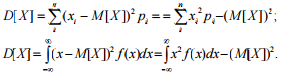
Свойства дисперсии: а) дисперсия постоянной величины равна нулю: D[C] = 0;
б) постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: D[CX] = C² D[X];
в) дисперсия алгебраической суммы нескольких независимых случайных величин равна сумме их дисперсий. Например, для трех случайных величин X₁, X₂, X₃ D[X1 ± Х2 ± Х3] = D[X1] + D[Х2] + D[Х3];

г) D[С ± Х] = D[X].
Модой дискретной случайной величины X (обозначается xmod) называется ее наиболее вероятное значение, то есть то значение, для которого вероятность pi достигает максимума. Моду дискретной случайной величины можно определить графически по столбцовой диаграмме, как абсциссу столбца, имеющего наибольшую высоту.
Модой непрерывной случайной величины X (обозначается xmod) называется то ее возможное значение, которому соответствует локальный максимум плотности распределения. В частности, если распределение имеет два максимума, то распределение называется двумодальным.
Медианой случайной величины X называется такое ее значение xmed, для которого
P(X < xmed) = P(X ≥ xmed) = 0,5, то есть одинаково вероятно, примет ли случайная величина значение, большее или меньшее медианы. Геометрически: медиана – это координата той точки на оси абсцисс, для которой площади фигур, ограниченных кривой f(x) и осью абсцисс, находящихся слева и справа от неё, одинаковы и равны 0,5. Учитывая определение функции распределения, F(xmed) = 0,5. Эта характеристика применяется, как правило, только для непрерывных случайных величин. Для дискретных случайных величин множество значений х, удовлетворяющих свойству медианы F(xmed) = 5,0, либо бесконечно, либо является пустым.
Для того чтобы получить характеристику разброса значений случайной величины относительно математического ожидания, имеющую такую же размерность, как и сама случайная величина, используют корень квадратный из дисперсии, взятый с положительным знаком. Полученная величина называется средним квадратическим отклонением и обозначается
Чем больше разброс значений случайной величины Х вокруг М[Х], тем больше σ[X ] и D[X ].
Коэффициент асимметрии (обозначается A[X]) характеризует скошенность распределения случайной величины относительно математического ожидания. Для симметричных относительно математического ожидания распределений A[X] = 0. Если в распределении случайной величины преобладают положительные отклонения, то A[X] > 0, если отрицательные, то A[X] < 0. Значение коэффициента асим- метрии для дискретных и непрерывных случайных величин вычисляется, соответственно по формулам:

Коэффициент эксцесса (обозначается Ex[X]) характеризует островершинность графика функции плотности распределения вероятностей f(x). Своеобразным началом отсчета при измерении степени островершинности служит нормальное распределение, для которого Ex[X] = 0. Как правило, распределения с более высокой и более острой вершиной кривой плотности распределения имеют положительное значение коэффициента эксцесса, а с более низкой и пологой – отрицательное значение. Для вычисления значений коэффициента эксцесса дискретных и непрерывных случайных величин используются формулы:

16. Законы распределения СВ. Биномиальный закон распределения.

Биномиальное распределение
Дискретная случайная величина X распределена по биномиальному закону, если возможные значения этой случайной величины 0, 1, 2,…, n, а вероятность каждого из значений определяется по формуле Бернулли:
где 0 ≤ p ≤ 1; q = 1 – p; m = 0, 1, 2,…, n.
Постоянные p и n, входящие в формулу, называются параметрами биномиального распределения.
На практике биномиальное распределения возникает при следующих условиях: пусть производится серия из n независимых испытаний, в каждом из которых событие A может осуществиться с вероятностью p. Тогда случайная величина X, определяющая число появлений события A в серии из n испытаний, распределена по биномиальному закону. Закон называется «биномиальным» потому, что правую часть равенства можно рассматривать как общий член разложения бинома Ньютона:

17. Законы распределения СВ. Закон распределения Пуассона.

Дискретная случайная величина X распределена по закону Пуассона, если ее возможные значения:
0, 1, 2, …, m,…, а соответствующие им вероятности задаются формулой:
(m =0,1,2...).
Закон распределения Пуассона зависит от одного параметра: a. Доказано, что для случайной величины, распределенной по закону Пуассона
Условия, при которых возникает распределение Пуассона.
1 Распределение Пуассона с параметром a = np можно приближенно применять вместо биномиального распределения, когда число испытаний n достаточно велико, а вероятность появления события в каждом испытании p очень мала (p < 0,1), то есть в каждом отдельном опыте событие A появляется крайне редко.
2 По закону Пуассона распределена случайная величина, описывающая число событий простейшего потока, произошедших в течение промежутка времени t.
Простейший поток событий. Потоком событий называется последовательность однородных событий, наступающих одно за другим в случайные моменты времени.
Интенсивностью потока λ называется среднее число событий, происходящих за единицу времени.