 |
Законы распределения СВ. Закон распределения Эрланга.
|
|
|
|
Пусть случайные величины ξ1, ξ2,, ξк независимы и имеют показательный закон распределения с одинаковым параметром λi = λ, т. е. ξi ~E (λ), i = 1. Тогда случайная величина ξ = ξ1 + ξ2 + + ξk имеет закон распределения Эрланга k -го порядка с параметром λ, т. е. ξ ~ ER(λ, k). Очевидно, что величина ξ не- прерывна и принимает лишь положительные значения.

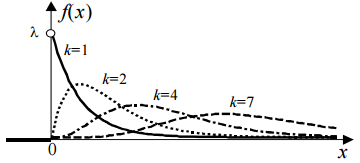
При k = 1 распределение Эрланга совпадает с показательным распределением. Основные числовые характеристики случайной величины ξ, имеющей закон распределения Эрланга, определяются выражениями: 
23. Предельные теоремы теории вероятностей
Предельные теоремы делятся на две группы: закон больших чисел, центральная предельная теорема.
Теоремы, относящих к закону больших чисел: неравенство Чебышева, теоремы Чебышева и Бернулли.
Теорема Лягунова отн. к центральной предельной теоремы.
Неравенство Чебышева
Если случайная величина X имеет конечное математическое ожидание и дисперсию, то для любого положительного числа τ справедливо неравенство P{|X−M(X)|⩽τ}>1−D[X]/τ2, то есть вероятность того, что отклонение случайной величины X от своего математического ожидания по абсолютной величине не превосходит τ и больше разности между единицей и отношением дисперсии этой случайной величины к квадрату τ. Неравенство Чебышева справедливо для любого закона распределения случайной величины X
и применимо как к положительным, так и к отрицательным случайным величинам.
Теорема Чебышева
При достаточно большом числе независимых испытаний n с вероятностью, близкой к единицы, можно утверждать, что разность между средним арифметическим наблюдавшихся значений случайной величины X
|
|
|
и математическим ожиданием этой величины M(X) по абсолютной величине окажется меньше сколь угодно малого числа τ>0 при условии, что случайная величина X имеет конечную дисперсию:
P{|X−M(X)|⩽τ}>1−η, где η — положительное число, близкое к единице.
Теорема Чебышева позволяет с достаточной точностью по средней арифметической судить о математическом ожидании или, наоборот, по математическому ожиданию предсказывать ожидаемую величину средней. Так, на основании этой теоремы можно утверждать, что если проведено достаточно большое количество измерений определённого параметра прибором, свободным от систематической погрешности, то средняя арифметическая результатов этих измерений сколь угодно мало отличается от истинного значения измеряемого параметра.
Теорема Бернулли
Теорема устанавливает связь между относительной частотой появления события и его вероятностью.
При достаточно большом числе независимых испытаний n с вероятностью, близкой к единице, можно утверждать, что разность между относительной частой появления события A в этих испытаниях е го вероятностью в отдельном испытании по абсолютной величине окажется меньше сколь угодно малого числа τ, если вероятность наступления этого события в каждом испытании постоянна и равна p.
Утверждение теоремы Бернулли можно записать в виде неравенства P{∣m/n−p∣⩽τ}>1−η, где r,η— любые сколь угодно малые положительные числа.
Понятие многомерной СВ.
Многомерной случайной величиной называется функция X (ω), определенная на множестве элементарных событий Ω, которая каждому элементарному исходу ω ставит в соответствие n действительных чисел. Таким образом многомерная случайная величина является совокупностью n одномерных величин.
Все компоненты многомерной дискретной случайной величины – одномерные дискретные случайные величины. Все компоненты многомерной непрерывной случайной величины – одномерные непрерывные случайные величины. Многомерные смешанные случайные величины содержат как дискретные, так и непрерывные компоненты. Основной характеристикой многомерной случайной величины является закон распределения, который может быть задан таблично, графически или аналитически (функция распределения, функция плотности распределения и т. д.).
|
|
|
25. Функция распределения двумерной СВ.
Функцией распределения двумерной случайной величины (ξ, η) называется функция F ξ η (x, y), равная вероятности того, что компонент ξ примет значение меньшее, чем x, а компонент η – значение меньшее, чем y, 
Таким образом, функция распределения двумерной случайной величины F ξ η (x, y) в точке (x, y) определяет вероятность, с которой двумерная случайная величина примет значение в нижнем левом квадранте относительно точки (x, y)

26. Функция плотности распределения двумерной СВ.
Функция распределения F ξ η (x, y) – наиболее универсальная форма закона распределения многомерных случайных величин как дискретных, так непрерывных и смешанных. Кроме этого, закон распределения непрерывных многомерных случайных величин может быть задан с помощью функции плотности распределения. Двумерная случайная величина называется непрерывной, если ее функция распределения
F ξ η (x, y)- непрерывная функция, дифференцируемая по каждому из аргументов, у которой существует вторая смешанная производная 
Аналогично тому, как была определена функция плотности распределения одномерной случайной величины, определим функцию плотности распределения F ξ η (x, y) непрерывной двумерной случайной величины как предел отношения вероятности попадания значения случайной величины (ξ, η) в элементарный прямоугольник, примыкающий к точке (x, y), к площади этого прямоугольника, когда оба его размера стремятся к нулю: 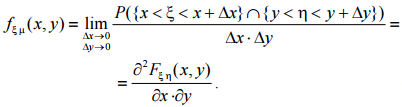
|
|
|


