 |
Третья задача на чувствительность
|
|
|
|
Изменение коэффициентов целевой функции, которые определяются ценами на готовую продукцию, оказывает влияние на наклон прямой, которая представляет эту функцию в принятой системе координат. Очевидно, что идентификация конкретной угловой точки в качестве оптимума зависит, прежде всего, от наклона этой прямой.
Это означает, что вариация коэффициентов целевой функции может привести к изменению совокупности связывающих ограничений и, следовательно, статуса того или иного ресурса (т. е. сделать недефицитный ресурс дефицитным, и наоборот).
Рассмотрим прямую (3) при изменении коэффициента 
.
Рисунок - 3. прямую (3) при изменении коэффициентов .
При уменьшении коэффициента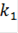 
прямая целевой функции будет вращаться против часовой стрелки вокруг точки В. Эта точка будет единственной точкой оптимального решения. Так прямая целевой функции будет вращаться, пока не совпадет с прямой (1). При этом 
.
При увеличении коэффициента 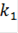прямая целевой функции будет вращаться по часовой стрелке вокруг точки D. Эта точка будет единственной точкой оптимального решения. Так прямая целевой функции будет вращаться, пока не совпадет с прямой (2). При этом 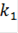стремится в бесконечность.
Таким образом, интервал изменения коэффициента :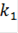 
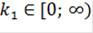
При увеличении коэффициента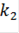 
прямая целевой функции будет вращаться против часовой стрелки вокруг точки В. Эта точка будет единственной точкой оптимального решения. Так прямая целевой функции будет вращаться, пока не совпадет с прямой (1). При этом 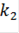стремится в бесконечность.
При уменьшении коэффициента 
прямая целевой функции будет вращаться по часовой стрелке вокруг точки D. Эта точка будет единственной точкой оптимального решения. Так прямая целевой функции будет вращаться, пока не совпадет с прямой (2). При этом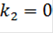 
.
|
|
|
Таким образом, интервал изменения коэффициента :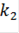 
Выводы
По завершению выполнения данной работы, а это - разбор задач на чувствительность, выяснили что: Дефицитными ресурсами в задаче являются максимальный суточный запас деталей и объем производства первой линии - эти ресурсы исчерпаны полностью. Рассмотрели увеличение максимального суточного запаса деталей. Таким образом, максимальный суточный запас деталей не следует увеличивать сверх того предела, когда соответствующее ему ограничение (3) становится избыточным. Изменение коэффициентов целевой функции, которые определяются ценами на готовую продукцию, оказывает влияние на наклон прямой, которая представляет эту функцию в принятой системе координат. Очевидно, что идентификация конкретной угловой точки в качестве оптимума зависит, прежде всего, от наклона этой прямой. Это означает, что вариация коэффициентов целевой функции может привести к изменению совокупности связывающих ограничений и, следовательно, статуса того или иного ресурса (т. е. сделать недефицитный ресурс дефицитным, и наоборот).
. На сколько можно увеличить запас некоторого ресурса для улучшения полученного оптимального значения целевой функции z?
При увеличении суточного запаса элементов до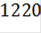 
единиц дальнейшее улучшение значения целевой функции становится невозможным.
. На сколько можно снизить запас некоторого ресурса при сохранении полученного оптимального значения целевой функции?
Снизить запас можно до 825 единиц.
Литература
Астафуров В.Г. Исследование операций, Томск 2002 г.
Р. М. Ларин А. В. Плясунов А. В. Пяткин Методы оптимизации. Примеры и задачи. учебное пособие. Новосибирск: Новосибирский государственный университет, 2003.
|
|
|
|
|
|
