 |
II. Криволинейные и поверхностные интегралы
|
|
|
|
Криволинейные интегралы
Рассмотрим на плоскости или в пространстве кривую L и функцию f, определенную в каждой точке этой кривой. Разобьем кривую на части Δ si длиной Δ si и выберем на каждой из частей точку Mi. Назовем d длину наибольшего отрезка кривой: 
.
Криволинейным интегралом первого рода от функции f по кривой L называется предел интегральной суммы 
, не зависящий ни от способа разбиения кривой на отрезки, ни от выбора точек Mi:
(24)
Если кривую L можно задать параметрически:
x = φ(t), y = ψ(t), z = χ(t), t0 ≤ t ≤ T,
то способ вычисления криволинейного интеграла первого рода задается формулой
(25)
В частности, если кривая L задана на плоскости явным образом:
у=φ (х), где х 1 ≤ х ≤ х 2, формула (40) преобразуется к виду:
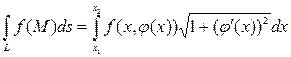. (26)
Теперь умножим значение функции в точке Mi не на длину i- го отрезка, а на проекцию этого отрезка, скажем, на ось О х, то есть на разность xi – xi- 1 = Δ xi.
Если существует конечный предел при 
интегральной суммы 
, не зависящий от способа разбиения кривой на отрезки и выбора точек Mi, то он называется криволинейным интегралом второго рода от функции f(M) по кривой L и обозначается
. (27)
Подобным образом можно определить и криволинейные интегралы 2-го рода вида
Если вдоль кривой L определены функции
P(M)=P(x, y, z), Q(M) = Q(x, y, z), R(M) = R(x, y, z),
которые можно считать компонентами некоторого вектора 
, и существуют интегралы
,
тогда их сумму называют криволинейным интегралом второго рода (общего вида) и полагают
. Если кривая L задана параметрическими уравнениями
x = φ(t), y = ψ(t), z = χ(t), α ≤ t ≤ β,
где φ, ψ, χ – непрерывно дифференцируемые функции, то
. (28)
Связь между двойным интегралом и криволинейным интегралом 2-го рода задается формулой Грина:
|
|
|
(29)
где L – замкнутый контур, а D – область, ограниченная этим контуром.
Необходимыми и достаточными условиями независимости криволинейного интеграла
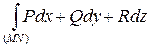
от пути интегрирования являются:
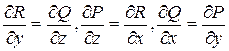. (30)
При выполнении условий (30) выражение Pdx + Qdy +Rdz является полным дифференциалом некоторой функции и. Это позволяет свести вычисление криволинейного интеграла к определению разности значений и в конечной и начальной точках контура интегрирования, так как
При этом функцию и можно найти по формуле
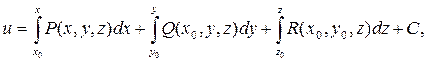(31)
где (x0, y0, z0) – точка из области D, a C – произвольная постоянная.
Поверхностные интегралы
Рассмотрим некоторую поверхность S, ограниченную контуром L, и разобьем ее на части S1, S2,…, Sп (при этом площадь каждой части тоже обозначим Sп). Пусть в каждой точке этой поверхности задано значение функции f(x, y, z). Выберем в каждой части Si точку
Mi (xi, yi, zi) и составим интегральную сумму
.
Если существует конечный предел при 
этой интегральной суммы, не зависящий от способа разбиения поверхности на части и выбора точек Mi, то он называется поверхностным интегралом первого рода от функции f(M) = f(x, y, z) по поверхности S и обозначается
. (32)
Если поверхность S задается явным образом, то есть уравнением вида z = φ(x, y), вычисление поверхностного интеграла 1-го рода сводится к вычислению двойного интеграла:
(33)
где Ω – проекция поверхности S на плоскость Оху.
Разобьем поверхность S на части S1, S2,…, Sп, выберем в каждой части Si точку Mi(xi, yi, zi), и умножим f(Mi) на площадь Di проекции части Si на плоскость О ху. Если существует конечный предел суммы
,
не зависящий от способа разбиения поверхности и выбора точек на ней, то он называется поверхностным интегралом второго рода от функции f(M) по выбранной стороне поверхности S и обозначается
(34)
Подобным образом можно проектировать части поверхности на координатные плоскости О xz и О yz. Получим два других поверхностных интеграла 2-го рода:
|
|
|
и 
.
Рассмотрев сумму таких интегралов по одной и той же поверхности соответственно от функций P(x, y, z), Q(x, y, z), R(x, y, z), получим поверхностный интеграл второго рода общего вида:
(35)
Если D, D΄ и D΄΄ - проекции поверхности S на координатные плоскости О ху, Oxz и Oyz, то
(36)
Связь между тройным интегралом по трехмерной области V и поверхностным интегралом 2-го рода по замкнутой поверхности S, ограничивающей тело V, задается формулой Гаусса-Остроградского:
(37)
где запись «S+» означает, что интеграл, стоящий справа, вычисляется по внешней стороне поверхности S.
Формула Стокса устанавливает связь между поверхностным интегралом 1-го рода по поверхности σ и криволинейным интегралом 2-го рода по ограничивающему ее контуру λ с учетом ориентации поверхности:
(38)
|
|
|
